- 2021-05-26 发布 |
- 37.5 KB |
- 4页
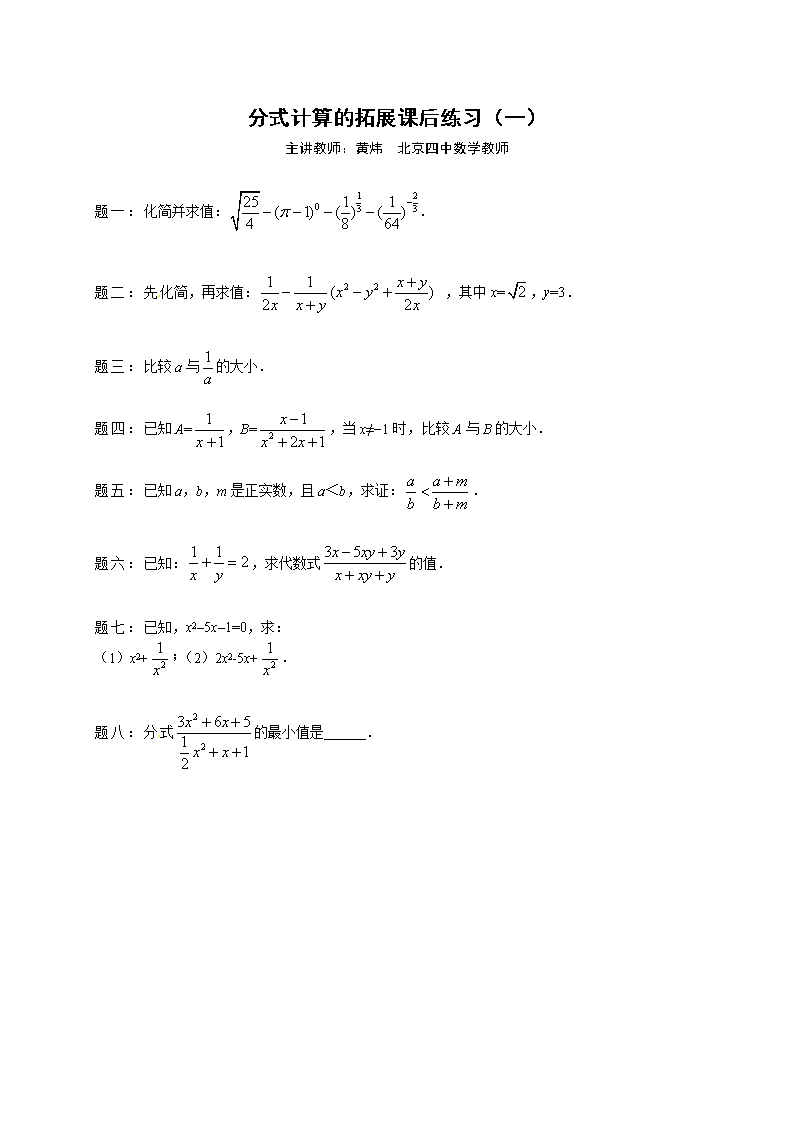
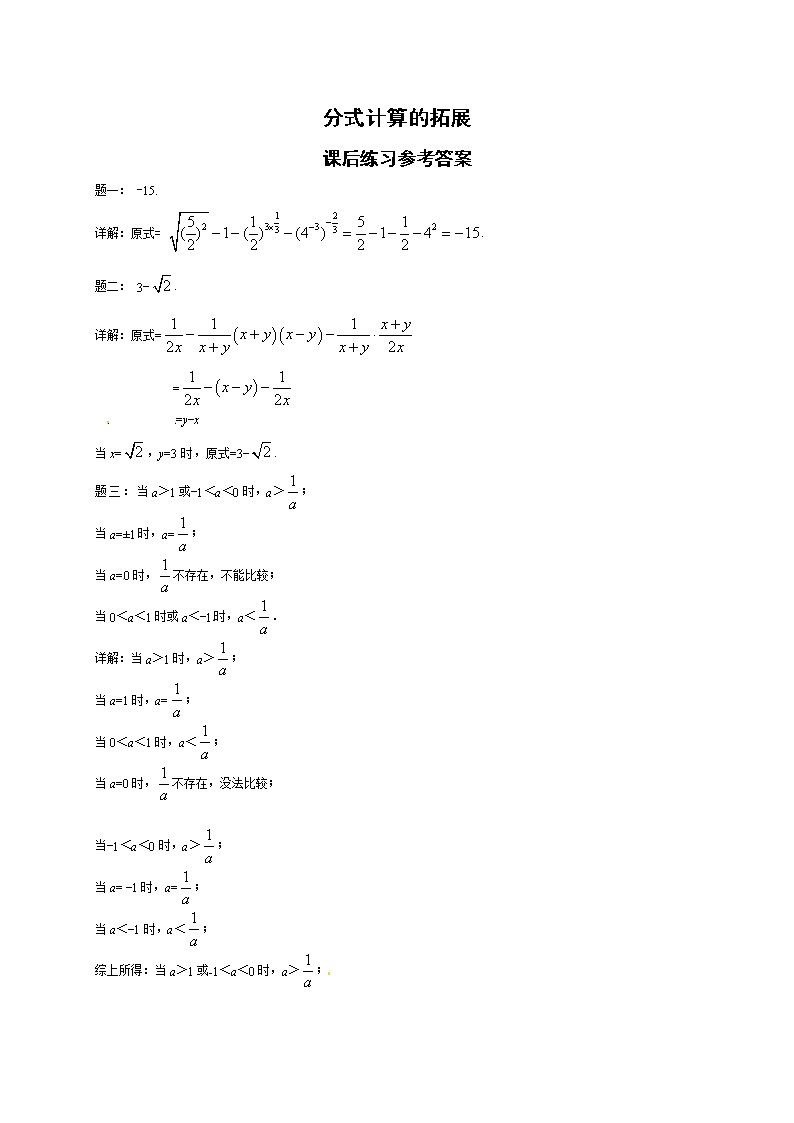

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学八年级下册分式计算的拓展 课后练习一及详解
分式计算的拓展课后练习(一) 主讲教师:黄炜 北京四中数学教师 题一: 化简并求值: 1 2 0 3 325 1 1( 1) ( ) ( )4 8 64 . 题二: 先 化简,再求值: 2 21 1 ( )2 2 x yx yx x y x ,其中 x= 2 ,y=3. 题三: 比较 a 与 1 a 的大小. 题四: 已知 A= 1 1x ,B= 2 1 2 1 x x x ,当 x≠1 时,比较 A 与 B 的大小. 题五: 已知 a,b,m 是正实数,且 a<b,求证: a a m b b m . 题六: 已知: 1 1 2x y ,求代数式 3 5 3x xy y x xy y 的值. 题七: 已知,x25x1=0,求: (1)x2+ 2 1 x (2)2x2-5x+ 2 1 x .[来源:www.shulihua.net] 题八: 分式 2 2 3 6 5 1 12 x x x x 的最小值是 . [ 来 源 : w w w . s h u l i h u a . n e t ] 分式计算的拓展 课后练习参考答案 题一: -15. 详解:原式= 1 2 2 3 3 23 35 1 5 1( ) 1 ( ) (4 ) 1 4 152 2 2 2 .[来源:www.shulihua.netwww.shulihua.net] 题二: 3 2 . 详解:原式= 1 1 1 2 2 x yx y x yx x y x y x = 1 1 2 2x yx x [来源:www.shulihua.net] =yx[来源:www.shulihua.netwww.shulihua.net] 当 x= 2 ,y=3 时,原式=3 2 . 题 三: 当 a>1 或1<a<0 时,a> 1 a ; 当 a=±1 时,a= 1 a ; 当 a=0 时, 1 a 不存在,不能比较; 当 0<a<1 时或 a<1时,a< 1 a . 详解:当 a>1 时,a> 1 a ; 当 a=1 时,a= 1 a ; 当 0<a<1 时,a< 1 a ; 当 a=0 时, 1 a 不存在,没法比较; 当1<a<0 时,a> 1 a ; 当 a= 1 时,a= 1 a ; 当 a<1 时,a< 1 a ; 综上所得:当 a>1 或-1<a<0 时,a> 1 a ; 当 a=±1 时,a= 1 a ; 当 a=0 时, 1 a 不存在,不能比较; 当 0<a<1 时或 a<1 时,a< 1 a . 题四: A>B. 详解:根据题意得: AB= 1 1x 2 1 2 1 x x x = 1 1x 2 1 ( 1) x x = 2 2 ( 1)x , 当 x≠1 时, 2 2 ( 1)x >0, 所以 AB>0,即 A>B. 题 五: a a m b b m 详解:由 a,b,m 是 正实数,故要证 a a m b b m 只要证 a(+m)<b(+m)只要证 ab+am<ab+bm, 只要证 am<bm,而 m>0,只要证 a<b, 由条件 a<b 成立,故原不等式成立. 题六: 1 3 . 详解:∵ 1 1 2x y 且 xy≠0 ∴x+y=2xy, ∴ 3 5 3x xy y x xy y = 3 5x y xy x y xy = 6 5 2 xy xy xy xy = 1 3 . 题七: 27;28. 详解:(1)∵x25x1=0, ∴x5 1 x =0, ∴x 1 x =5, ∴两边平方得:x2-2+ 2 1 x =25, x2+ 2 1 x =27; (2)∵x25x1=0, ∴x25x=1, ∴2x2-5x+ 2 1 x =x25x+x2+ 2 1 x =1+27=28. 题八: 4. 详解:令 y= 2 2 3 6 5 1 12 x x x x = 2 26 2 2x x , 问题转化为考虑函数 z=x2+2x+2 的最小值, ∵z=x2+2x+2=(x+1)2+1 ∴当 x=1 时,zmin=1, ∴ymin=62=4, 即分式 2 2 3 6 5 1 12 x x x x 的最小值是 4.查看更多