2020年湖北省黄冈八模高考数学模拟试卷(文科)(四)
2020年湖北省黄冈八模高考数学模拟试卷(文科)(四)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合A={y|y=1−x2, x∈[−1, 1]},B={x|y=x+2},则A∩B=( )
A.[0, 1] B.[−1, 1] C.(0, 1) D.⌀
2. 若复数z满足(3−4i)z=5(1−i),其中i为虚数单位,则z的虚部为( )
A.1 B.−15 C.15 D.−1
3. 已知a=log20.2,b=20.2,c=0.20.3,则( )
A.a
0,函数f(x)=cos(ωx+π4)在(π2, π)上单调递增,则ω的取值范围是( )
A.[12, 54] B.[12, 74] C.[34, 94] D.[32, 74]
11. 在平面直角坐标系中,A(−2, 0),B(1, 3),O为坐标原点,且OM→=αOA→+βOB→(α+β=1),N(1, 0),则|MN→|的最小值为( )
A.22 B.322 C.92 D.32
第21页 共22页 ◎ 第22页 共22页
12. 设在R上可导的函数f(x)满足f(0)=0,f(x)−f(−x)=13x3,并且在(−∞, 0)上有f′(x)<12x2,实数a满足f(6−a)−f(a)≥−13a3+3a2−18a+36,则实数a的取值范围是( )
A.(−∞, 3] B.[3, +∞) C.[4, +∞] D.(−∞, 4]
二、填空题:本题共4小题,每小题5分,共20分.
命题“∀x>1,都有x2+1>2”的否定是________.
设x,y满足约束条件:x≥0,y≥0x−y≥−1x+y≤3 ,则z=x−10y的取值范围是________.
已知△ABC各角的对应边分别为a,b,c,且满足ba+c+ca+b≥1,则角A的取值范围是________.
将正三棱锥P−ABC置于水平反射镜面上,得一“倒影三棱锥”P−ABC−Q,如图,下列关于该“倒影三棱锥”的说法中,正确的有________.
①PQ⊥平面ABC;
②若P,A,B,C在同一球面上,则Q也在该球面上;
③若该“倒影三棱锥”存在外接球,则AB=2PA;
④若AB=62PA,则PQ的中点必为“倒影三棱锥”外接球的球心.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.
已知等差数列{an}满足(a1+a2)+(a2+a3)+⋯+(an+an+1)=2n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
(2)数列{bn}中,b1=1,b2=2,从数列{an}中取出第bn项记为cn,若{cn}是等比数列,求{bn}的前n项和Tn.
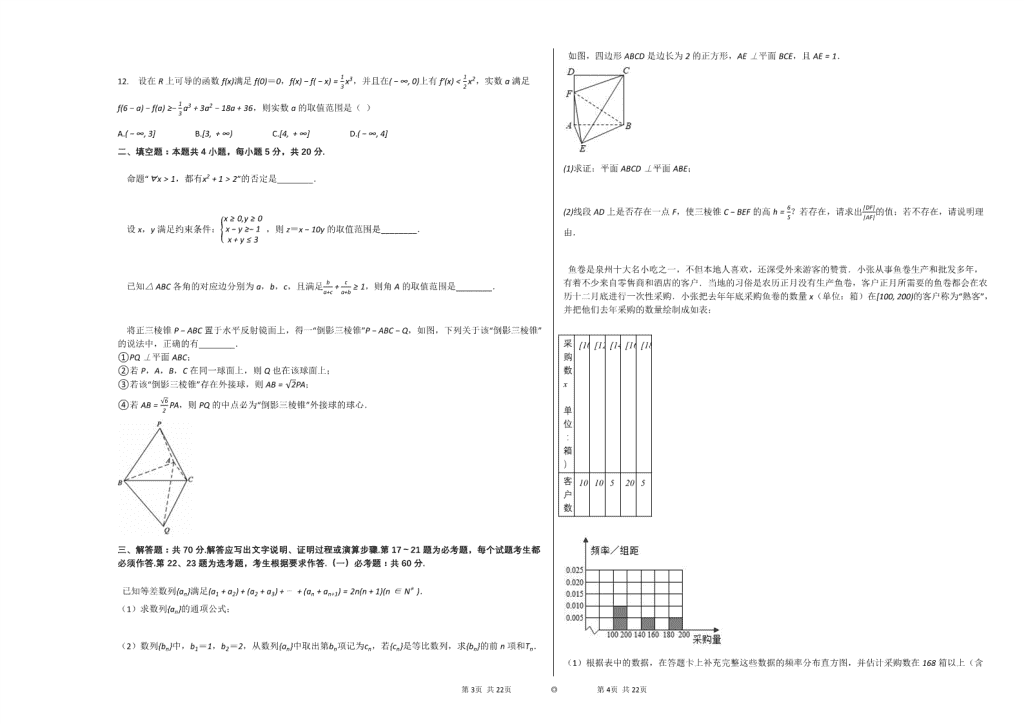
如图,四边形ABCD是边长为2的正方形,AE⊥平面BCE,且AE=1.
(1)求证:平面ABCD⊥平面ABE;
(2)线段AD上是否存在一点F,使三棱锥C−BEF的高h=65?若存在,请求出|DF||AF|的值;若不存在,请说明理由.
鱼卷是泉州十大名小吃之一,不但本地人喜欢,还深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户.当地的习俗是农历正月没有生产鱼卷,客户正月所需要的鱼卷都会在农历十二月底进行一次性采购.小张把去年年底采购鱼卷的数量x(单位:箱)在[100, 200)的客户称为“熟客”,并把他们去年采购的数量绘制成如表:
采购数x(单位:箱)
[100, 120)
[120, 140)
[140, 160)
[160, 180)
[180, 200)
客户数
10
10
5
20
5
(1)根据表中的数据,在答题卡上补充完整这些数据的频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的58,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值作代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若没有在网上出售鱼卷,则按去年的价格出售,每箱利润为20
第21页 共22页 ◎ 第22页 共22页
元,预计销售量与去年持平;若计划在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元(2≤m≤5)销售量可增加1000m箱,求小张在今年年底收入Y(单位:元)的最大值.
如图,已知A(−1, 0),B(1, 0)Q、G分别为△ABC的外心、重心,QG // AB.
(1)求点C的轨迹E的方程.
(2)是否存在过P(0, 1)的直线L交曲线E与M,N两点且满足MP→=2PN→,若存在求出L的方程,若不存在请说明理由.
已知函数f(x)=|x−a|−lnx(a>0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)比较ln2222+ln3232+⋯+lnn2n2与(n−1)(2n+1)2(n+1)的大小(n∈N+且n>2),并证明你的结论.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]
在平面直角坐标系xOy中,A点的直角坐标为(3+2cosα,1+2sinα)(α为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,直线的极坐标方程为2ρcos(θ+π6)=m.(m为实数).
(1)试求出动点A的轨迹方程(用普通方程表示)
(2)设A点对应的轨迹为曲线C,若曲线C上存在四个点到直线的距离为1,求实数m的取值范围.
[选修4-5:不等式选讲](共1小题,满分0分)
设函数f(x)=x−|x+2|−|x−3|−m,若∀x∈R,1m−4≥f(x)恒成立.
(1)求m的取值范围;
(2)求证:log(m+1)(m+2)>log(m+2)(m+3).
第21页 共22页 ◎ 第22页 共22页
参考答案与试题解析
2020年湖北省黄冈八模高考数学模拟试卷(文科)(四)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】
A
【考点】
交集及其运算
【解析】
可以求出集合A,B,然后进行交集的运算即可.
【解答】
∵ A=[0, 1],B=[−2, +∞),
∴ A∩B=[0, 1].
2.
【答案】
C
【考点】
复数的运算
【解析】
把已知等式变形,再由复数代数形式的乘除运算化简得答案.
【解答】
由(3−4i)z=5(1−i),
得z=5(1−i)3−4i=5(1−i)(3+4i)(3−4i)(3+4i)=5(7+i)25=75+15i.
∴ z的虚部为15.
3.
【答案】
B
【考点】
指数式、对数式的综合比较
【解析】
由指数函数和对数函数的单调性易得log20.2<0,20.2>1,0<0.20.3<1,从而得出a,b,c的大小关系.
【解答】
解:a=log20.220=1,
∵ 0<0.20.3<0.20=1,
∴ c=0.20.3∈(0, 1),
∴ a0,
∴ k=1,
∴ ω∈[32, 74].
11.
【答案】
B
【考点】
第21页 共22页 ◎ 第22页 共22页
向量的共线定理
点到直线的距离公式
【解析】
由题意知A,B,M共线,先求出直线AB的方程,再根据点到直线的距离公式,点N到直线的距离为d,即为|MN→|的最小值.
【解答】
解:如图
∵ OM→=αOA→+βOB→(α+β=1),
∴ A,B,M共线,
∵ A(−2, 0),B(1, 3),
∴ 直线AB的方程为x−y+2=0,
∵ N(1, 0),设点N到直线的距离为d,
∴ d=|1−0+2|1+1=322
∴ |MN→|的最小值为N到直线AB的距离322,
故选B.
12.
【答案】
A
【考点】
利用导数研究函数的单调性
【解析】
依题意,构造函数g(x)=f(x)−16x3,可知函数g(x)为偶函数且在(−∞, 0)上单调递减,在(0, +∞)上单调递增,进而题设不等式等价于g(6−a)≥g(a),即|6−a|≥|a|,解出即可求得实数a的取值范围.
【解答】
设g(x)=f(x)−16x3,则g′(x)=f′(x)−12x2<0(x<0),
故g(x)=f(x)−16x3在区间(−∞, 0)上单调递减,
又g(x)−g(−x)=f(x)−16x3−[f(−x)+16x3]=0,故函数g(x)为偶函数,在区间(0, +∞)上单调递增,
而g(6−a)−g(a)=f(6−a)−f(a)−(−13a3+3a2−18a+36)≥0,故原不等式等价于g(6−a)≥g(a),即|6−a|≥|a|,解得a≤3.
二、填空题:本题共4小题,每小题5分,共20分.
【答案】
∃x>1,有x2+1≤2
【考点】
命题的否定
【解析】
根据全称命题的否定是特称命题,进行判断即可.
【解答】
全称命题的否定是特称命题,
得命题的否定是:∃x>1,有x2+1≤2,
【答案】
[−19, 3]
【考点】
简单线性规划
【解析】
作出不等式组对应的平面区域,利用目标函数的几何意义,结合数形结合进行求解即可
【解答】
由z=x−10y得y=110x−110z,
作出不等式组对应的平面区域如图(阴影部分):
平移直线y=110x−110z,
由图象可知当直线y=110x−110z,过点A(3, 0)时,
直线y=110x−110z的截距最小,此时z最大为z=3−0=3,
由图象可知当直线y=110x−110z,
过点B时,直线y=110x−110z的截距最大,此时z最小,
由x−y=−1x+y=3 ,解得x=1y=2 ,即B(1, 2),
代入目标函数z=x−10y,得z=1−10×2=−19,
故−19≤z≤3,
【答案】
(0, π3]
【考点】
不等式的证明
【解析】
将已知不等式化简整理,再由余弦定理,可得cosA≥12(0240000,
∴ 小张在今年年底收入Y(单位:元)的最大值为256000(元)
【考点】
频率分布直方图
【解析】
(1)根据统计表和直方图即可求出,
(2)根据统计表和直方图即可求出,
(3)没有在网上出售鱼卷,则今年的年底小张的收入为12000×20=240000(元),若网上出售鱼卷,则今年的年底的销售量为12000+1000m,即可求出Y的最大值,比较即可
【解答】
由表一数据,补出值如图如右:
根据上图,可知采购量在168以上的客户端数量为:
20×20×(0.005+0.020×180−16820)=17人,
由图一可知,去年年底“熟客”所采购的鱼卷总数大约为:
110×10+120×10+150×5+17−×20+190×5=7500(箱),
∴ 小张去年年底总的销售量为7500÷58=12000(箱).
若没有在网上出售鱼卷,则今年的年底小张的收入为12000×20=240000(元),
第21页 共22页 ◎ 第22页 共22页
若网上出售鱼卷,则今年的年底的销售量为12000+1000m(箱),每箱的利润为20−m(元),
则今年的年底小张的收入为Y=(20−m)(12000+1000m)
=1000(−m2+8m+240)=1000[−(m−4)2+256]=256000(元),
∵ 256000>240000,
∴ 小张在今年年底收入Y(单位:元)的最大值为256000(元)
【答案】
设C(x, y)(y≠0).则G(x3,y3),由于QG // AB则Q(0,y3),
由|QA|=|QC|⇒1+y29=x2+4y29⇒x2+y23=1①,
故轨迹E的方程为x2+y23=1(y≠0).
当L与y轴重合时不符合条件.假设存在直线L:y=kx+1,
设M(x1, y1),N(x2, y2)
联立y=kx+1x2+y23=1,则有(3+k2)+2kx−2=0,
x1+x2=−2k3+k2,x1⋅x2=−23+k2
由于MP→=2PN→则有x1=−2x2,即x1x2=−2,
(x1+x2)2x1x2=(4k23+k2)2⋅(−3+k22)=−2k23+k2
由于(x1+x2)2x1x2=x1x2+x2x1+2=−12则有k2=1即k=±1,
则直线L过(−1, 0),或(1, 0),
轨迹E的方程为x2+y23=1(y≠0).
所以直线L不存在.
【考点】
椭圆的应用
轨迹方程
直线与椭圆的位置关系
【解析】
(1)设出G的坐标,椭圆向量相等,转化求解轨迹方程即可.
(2)设出直线方程与椭圆方程联立,利用韦达定理,结合向量关系,转化求解即可.
【解答】
设C(x, y)(y≠0).则G(x3,y3),由于QG // AB则Q(0,y3),
由|QA|=|QC|⇒1+y29=x2+4y29⇒x2+y23=1①,
故轨迹E的方程为x2+y23=1(y≠0).
当L与y轴重合时不符合条件.假设存在直线L:y=kx+1,
设M(x1, y1),N(x2, y2)
联立y=kx+1x2+y23=1,则有(3+k2)+2kx−2=0,
x1+x2=−2k3+k2,x1⋅x2=−23+k2
由于MP→=2PN→则有x1=−2x2,即x1x2=−2,
(x1+x2)2x1x2=(4k23+k2)2⋅(−3+k22)=−2k23+k2
由于(x1+x2)2x1x2=x1x2+x2x1+2=−12则有k2=1即k=±1,
则直线L过(−1, 0),或(1, 0),
轨迹E的方程为x2+y23=1(y≠0).
所以直线L不存在.
【答案】
第21页 共22页 ◎ 第22页 共22页
(1)函数f(x)可化f(x)=x−lnx−a,x≥aa−x−lnx,01时,f′(x)>0,故f(x)在[a, 1)上递减,
在(1, +∞)上递增,而f(x)在x=a处连续,
所以当a≥1时,f(x)在(0, a)上递减,在[a, +∞)上递增;
当01时,x−1−lnx>0,即lnx>1−x,
所以lnxx<1−1x.
所以ln2222+ln3232+⋯+lnn2n2<1−122+1−132+⋯1−1n2,
=n−1−(122+132+⋯+1n2),
1−x,在区间(1, 2)上恒成立,利用导数求出g(x)的最小值,只要最小值大于0即可.
【解答】
(1)函数f(x)可化f(x)=x−lnx−a,x≥aa−x−lnx,01时,f′(x)>0,故f(x)在[a, 1)上递减,
在(1, +∞)上递增,而f(x)在x=a处连续,
所以当a≥1时,f(x)在(0, a)上递减,在[a, +∞)上递增;
当01时,x−1−lnx>0,即lnx>1−x,
所以lnxx<1−1x.
所以ln2222+ln3232+⋯+lnn2n2<1−122+1−132+⋯1−1n2,
=n−1−(122+132+⋯+1n2),
0;
证明:m>0,可得m+3>m+2>m+1>1,
则lg(m+3)>lg(m+2)>lg(m+1)>lg1=0,
∵ lg(m+1)lg(m+3)<[lg(m+1)+lg(m+3)2]2=[lg(m+1)(m+3)]24lg(m+3)lg(m+2),
∴ log(m+1)(m+2)>log(m+2)(m+3).
【考点】
绝对值三角不等式
绝对值不等式的解法与证明
【解析】
(1)由∀x∈R,1m−4≥f(x)恒成立,可得m+1m≥x−|x+2|−|x−3|+4,求出右边的最大值,即可求m的取值范围;
(2)利用对数的性质及基本不等式,即可证明结论.
【解答】
∵ ∀x∈R,1m−4≥f(x)恒成立,
∴ m+1m≥x−|x+2|−|x−3|+4,
令g(x)=x−|x+2|−|x−3|+4,则g(x)在(−∞, 3)上是增函数,
(3, +∞)上是减函数,g(x)max=g(3)=2,
∴ m+1m≥2,∴ m>0;
证明:m>0,可得m+3>m+2>m+1>1,
则lg(m+3)>lg(m+2)>lg(m+1)>lg1=0,
∵ lg(m+1)lg(m+3)<[lg(m+1)+lg(m+3)2]2=[lg(m+1)(m+3)]24lg(m+3)lg(m+2),
∴ log(m+1)(m+2)>log(m+2)(m+3).
第21页 共22页 ◎ 第22页 共22页