- 2021-05-26 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级数学下册第5章《相交线与平行线》检测2(新版)新人教版
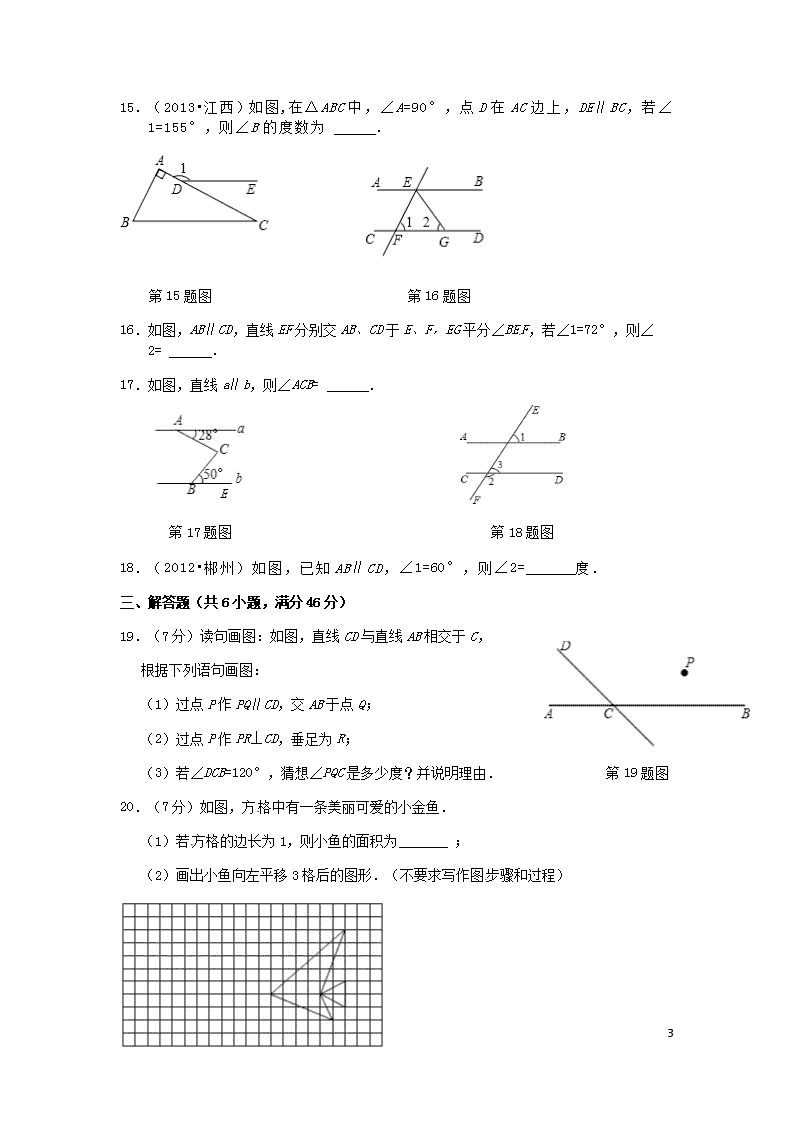
1 第五章 相交线与平行线检测题 (时间:90 分钟,满分:100 分) 一、选择题(每小题 3 分,共 30 分) 1.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行; ③相等的角是对顶角;④同位角相等.其中错误的有( ) A.1 个 B.2 个 C.3 个 D.4 个 2.点 P 是直线 l 外一点,A 为垂足, ,且 PA=4 cm,则点 P 到直线 l 的距离( ) A.小于 4 cm B.等于 4 cm C.大于 4 cm D.不确定 3.(2013•安徽)如图,AB∥CD,∠A+∠E=75°,则∠C 为( ) A.60° B.65° C.75° D.80° 第 3 题图 第 4 题图 4.(2013•襄阳)如图,BD 平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD 的度数 为( ) A.55° B.50° C.45° D.40° 5.(2013•孝感)如图,∠1=∠2,∠3=40°,则∠4 等于( ) A.120° B.130° C.140° D.40° 6.如图,AB∥CD,AC⊥BC,图中与∠CAB 互余的角有( ) A.1 个 B.2 个 C.3 个 D.4 个 第 5 题图 第 6 题图 7.如图,点在的延长线上,下列条件中不能判定 AB∥CD 的是( ) A.∠1=∠2 B.∠3=∠4 2 C.∠5=∠ D.∠+∠BDC=180° 第 7 题图 第 8 题图 8.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB 相等的角的个数为( ) A.2 个 B.3 个 C.4 个 D.5 个 9. 下列条件中能得到平行线的是( ) ①邻补角的角平分线;②平行线内错角的角平分线;③平行线同旁内角的角平分线. A.①② B.②③ C.② D.③ 10. 两平行直线被第三条直线所截,同位角的平分线( ) A.互相重合 B.互相平行 C.互相垂直 D.相交 二、填空题(共 8 小题,每小题 3 分,满分 24 分) 11.如图,直线 a、b 相交,∠1=,则∠2= . 第 11 题图 12.(2013•镇江)如图,AD 平分△ABC 的外角∠EAC,且 AD∥BC,若∠BAC=80°, 则∠B= °. 第 12 题图 第 13 题图 第 14 题 图 13.如图,计划把河水引到水池 A 中,先作 AB⊥CD,垂足为 B,然后沿 AB 开渠,能使所开 的渠道最短,这样设计的依据是 . 14.如图,直线 AB,CD,EF 相交于点 O,且 AB⊥CD,∠1 与∠2 的关系是 . 3 15.(2013•江西)如图,在△ABC 中,∠A=90°,点 D 在 AC 边上,DE∥BC,若∠ 1=155°,则∠B 的度数为 . 第 15 题图 第 16 题图 16.如图,AB∥CD,直线 EF 分别交 AB、CD 于 E、F,EG 平分∠BEF,若∠1=72°,则∠2= . 17.如图,直线 a∥b,则∠ACB= . 第 17 题图 第 18 题图 18.(2012•郴州)如图,已知 AB∥CD,∠1=60°,则∠2= 度. 三、解答题(共 6 小题,满分 46 分) 19.(7 分)读句画图:如图,直线 CD 与直线 AB 相交于 C, 根据下列语句画图: (1)过点 P 作 PQ∥CD,交 AB 于点 Q; (2)过点 P 作 PR⊥CD,垂足为 R; (3)若∠DCB=120°,猜想∠PQC 是多少度?并说明理由. 第 19 题图 20.(7 分)如图,方格中有一条美丽可爱的小金鱼. (1)若方格的边长为 1,则小鱼的面积为 ; (2)画出小鱼向左平移 3 格后的图形.(不要求写作图步骤和过程) 4 第 20 题图 21.(8 分)已知:如图,∠BAP+∠APD =,∠1 =∠2.求证:∠E =∠F. 第 21 题图 第 22 题图 22.(8 分)已知:如图,∠1 =∠2,∠3 =∠4,∠5 =∠6.求证:ED ∥FB. 23.(8 分)如图,CD 平分∠ACB,DE∥BC,∠AED=80°,求∠EDC 的度数. 第 23 题图 第 24 题图 24.(8 分)如图,已知 AB∥CD,∠B=65°,CM 平分∠BCE,∠MCN=90°,求∠DCN 的度数. 5 第五章 相交线与平行线检测题参考答案 1.B 解析:①是正确的,对顶角相等; ②正确,在同一平面内,垂直于同一条直线的两直线平行; ③错误,角平分线分成的两个角相等但不是对顶角; ④错误,同位角只有在两直线平行的情况下才相等. 故①②正确,③④错误,所以错误的有两个, 故选 B. 2. B 解析:根据点到直线的距离为点到直线的垂线段的长度(垂线段最短), 所以点 P 到直线 l 的距离等于 4 cm,故选 B. 3. C 解析:∵∠A+∠E=75°, ∴∠EOB=∠A+∠E=75°. ∵AB∥CD,∴∠C=∠EOB=75°,故选 C. 4. A 解析:∵CD∥AB,∴∠ABC+∠DCB=180°. ∵∠BCD=70°,∴∠ABC=180°-70°=110°. ∵BD 平分∠ABC,∴∠ABD=55°. 5. C 解析:如题图所示,∵∠1=∠2, ∴a∥b,∴∠3=∠5. ∵∠3=40°,∴∠5=40°, ∴∠4=180°-∠5=180°-40°=140°, 故选 C. 6. C 解析:∵ AB∥CD,∴ ∠ABC=∠BCD. 设∠ABC 的对顶角为∠1,则∠ABC=∠1. 又∵ AC⊥BC,∴ ∠ACB=90°, ∴ ∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°, 因此与∠CAB 互余的角为∠ABC,∠BCD,∠1. 故选 C. 7. A 解析:选项 B 中,∵ ∠3=∠4,∴ AB∥CD (内错角相等,两直线平行),故正确; 6 选项 C 中,∵ ∠5=∠B,∴ AB∥CD (内错角相等,两直线平行),故正确; 选项 D 中,∵ ∠B+∠BDC=180°,∴ AB∥CD(同旁内角互补,两直线平行),故正确; 而选项 A 中,∠1 与∠2 是直线 AC、BD 被直线 AD 所截形成的内错角,∵ ∠1=∠2,∴ AC ∥BD,故 A 错误.选 A. 8. D 解析 :如题图所示,∵ DC∥EF,∴ ∠DCB=∠EFB. ∵ DH∥EG∥BC, ∴ ∠GEF=∠EFB,∠DCB=∠HDC,∠DCB=∠CMG=∠DME, 故与∠DCB 相等的角共有 5 个.故选 D. 9. C 解析 :结合已知条件,利用平行线的判定定理依次推理判断. 10. B 解析:∵ 两条平行直线被第三条直线所截,同位角相等, ∴ 它们角的平分线形成的同位角相等,∴ 同位角相等的平分线平行. 故选 B. 11. 144° 解析:由题图得,∠1 与∠2 互为邻补角,即∠1+∠2=180°. 又∵∠1=36°,∴ ∠2=180°36°=144°. 12. 50 解析:∵∠BAC=80°,∴∠EAC=100°. ∵AD 平分△ABC 的外角∠EAC,∴∠EAD=∠DAC=50°. ∵AD∥BC,∴∠B=∠EAD=50°. 故答案为 50. 13. 垂线段定理:直线外一点与直线上所有点的连线中,垂线段最短 解析:根据垂线段定理,直线外一点与直线上所有点的连线中,垂线段最短, ∴ 沿 AB 开渠,能使所开的渠道最短. 14. ∠1+∠2=90° 解析:∵ 直线 AB、EF 相交于 O 点,∴ ∠1=∠DOF. 又∵ AB⊥CD,∴ ∠2+∠DOF=90°,∴ ∠1+∠2=90°. 15. 65° 解析:∵∠1=155°,∴∠EDC=180°-155°=25°. ∵DE∥BC,∴∠C=∠EDC=25°. ∵在△ABC 中,∠A=90°,∠C=25°, 7 ∴ ∠B=180°-90°-25°=65°. 故答案为 65°. 16. 54° 解析:∵ AB∥CD, ∴ ∠BEF=180°∠1=180°72°=108°,∠2=∠BEG. 又∵ EG 平分∠BEF,∴ ∠BEG=∠BEF=×108°=54°, 故∠2=∠BEG=54°. 17. 78° 解析:延长 BC 与直线 a 相交于点 D, ∵ a∥b,∴ ∠ADC=∠DBE=50°. ∴ ∠ACB=∠ADC +28°=50°+28°=78°. 故应填 78°. 18. 120 解析:∵AB∥CD,∴∠1=∠3, 而∠1=60°,∴∠3=60°. 又∵∠2+∠3=180°,∴∠2=180°-60°=120°. 故答案为 120. 19.解:(1)(2)如图所示. 第 19 题答图 (3)∠PQC=60°. 理由:∵ PQ∥CD,∴ ∠DCB+∠PQC=180°. ∵ ∠DCB=120°,∴ ∠PQC=180°120°=60°. 20. 解:(1)小鱼的面积为 7×6 2 1 ×5×6 2 1 ×2×5 2 1 ×4×2 2 1 ×1.5×1 2 1 × 2 1 ×11=16. (2)将每个关键点向左 平移 3 个单位,连接即可. 8 第 20 题答图 21.证明:∵ ∠BAP+∠APD = 180°,∴ AB∥CD.∴ ∠BAP =∠APC. 又∵ ∠1 =∠2,∴ ∠BAP−∠1 =∠APC−∠2. 即∠EAP =∠APF.∴ AE∥FP.∴ ∠E =∠F. 22.证明:∵ ∠3 =∠4,∴ AC∥BD.∴ ∠6+∠2+∠3 = 180°. ∵ ∠6 =∠5,∠2 =∠1,∴ ∠5+∠1+∠3 = 180°. ∴ ED∥FB. 23. 解:∵ DE∥BC,∠AED=80°,∴ ∠EDC=∠BCD,∠ACB=∠AED=80°. ∵ CD 平分∠ACB, ∴ ∠BCD= 2 1 ∠ACB=40°,∴ ∠EDC=∠BCD=40°. 24. 解:∵ AB∥CD,∴ ∠B+∠BCE=180°(两直线平行,同旁内角互补). ∵ ∠B=65°,∴ ∠BCE=115°. ∵ CM 平分∠BCE,∴ ∠ECM= 2 1 ∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°,∠MCN=90°, ∴ ∠NCD=180°-∠ECM-∠MCN=180°-57.5°-90°=32.5°.查看更多