八年级上数学课件《勾股定理的简单应用》 (14)_苏科版

八年级上数学课件《勾股定理的简单应用》 (14)_苏科版

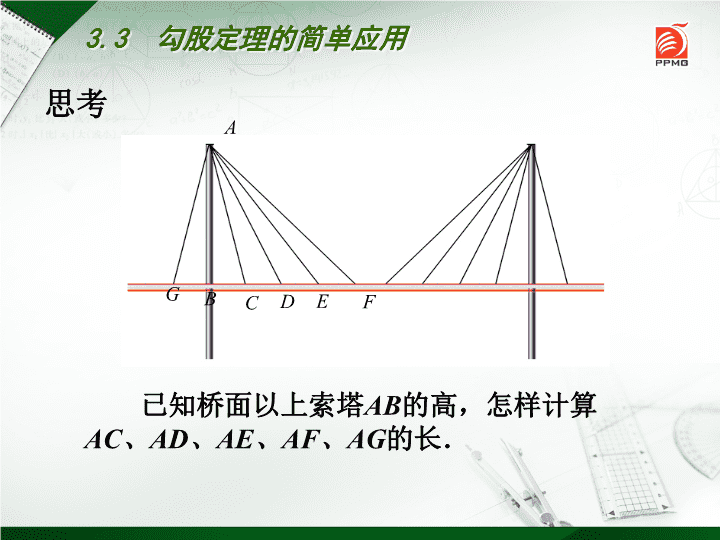
八年级(上册)初中数学 3.3　 勾股定理的简单应用 图片欣赏 　　从远处看，斜拉桥的索塔、桥面与拉索组 成许多直角三角形． 3.3　勾股定理的简单应用 思考 　　已知桥面以上索塔AB的高，怎样计算 AC、AD、AE、AF、AG的长． 3.3　勾股定理的简单应用 A B C E FG D A C B 直角三角形两直角边的平方 和等于斜边的平方。 在△ABC中，若∠C=90°， 则有a²+b²=c². 如果三角形的三边长a，b，c， 且a²+b²=c²，那么这个三角 形是直角三角形。 互逆 命题 满足关系a²+b²=c²的3个正整 数a,b,c称为勾股数。 如：3，4，5；6，8，10；5，12，13； b c a 例1　《九章算术》中的“折竹”问题：今有竹高 一丈，末折抵地，去根三尺，问折者高几何？ 意思是：有一根竹子原高1丈 （1丈＝10尺），中部有一处折 断，竹梢触地面处离竹根3尺， 试问折断处离地面多高？ 3.3　勾股定理的简单应用 解：如图，我们用线段OA和线段 AB来表示竹子，其中线段AB表示 竹子折断部分，用线段OB来表示 竹梢触地处离竹根的距离． ∵∠AOB＝90°， ∴OA2＋OB2＝AB2， ∴x2＋32＝（10－x）2． A O B x (10－x) 3 3.3　勾股定理的简单应用 设OA＝x，则AB＝10－x． 方程思想 意思是：有一根竹子原高1丈 （1丈＝10尺），中部有一处 折断，竹梢触地面处离竹根3 尺，试问折断处离地面多高？ 长方形ABCD如图折叠，使点D落在BC边上的点F 处，已知AB=8，BC=10，求折痕AE的长。 A B C D F E8 10 8 10 10 6 x x 8-x 4 ? 2 2 24 (8 )x x   2 216 64 16x x x    5x 解得 变式: 折叠问题 方程思想 125105 22 22   AFEFAE 3.3　勾股定理的简单应用 • 例2　如图，在△ABC中，AB＝26，BC＝20， BC边上的中线AD＝24，求AC. D CB A 解:∵AD是BC边上的中线， ∴BD＝CD＝ BC＝ ×20＝10． ∴AD2＋BD2＝576+100＝676， AB 2＝262＝676， ∴AD2＋BD2＝AB2， ∴ ∠ADB＝90°，即AD垂直平分BC． ∴AC＝AB＝26. 1 2 1 2 用勾股定理逆定理判定直角 26 20 24 10 10 ∵AD=24,AB=26,BD=10 如图，在△ABC中，AB=3,AC=5,AD是边BC 上的中线，AD=ED=2，求△ABC的面积。 练习: A BC D E 35 2 23 勾股定理主要应用于求线段的长度，进而可 求图形的周长、面积等； 3.3　勾股定理的简单应用 勾股定理的逆定理用于判断三角形的形状． 有一圆柱，底面圆的周长为16cm，高为6cm，一只蚂 蚁从底面的A处爬行到对角B处吃食物，它爬行的最 短路线长为多少？ A B B A C 例3： 8 6 利用展开图化曲为直计 算路程最短问题 10 如果盒子换成如图长为3cm，宽为2cm， 高为1cm的长方体，蚂蚁沿着表面需要爬 行的最短路程又是多少呢？ A B 3 2 1 探索研究： 分析：有3种情况,六条路线。 (1)经过前面和上底面; (或经过后面和下底面) (2)经过前面和右面; (或经过左面和后面) (3)经过左面和上底面. (或经过下底面和右面) A B 2 3A B 1 C 3 2 1 B CA 3 2 1 B CA 3 2 1 A B b c a 延伸提高: 如果长方形的长、宽、高分别是a、b、c（a＞b＞ c），你能求出蚂蚁从顶点A到B的最短路径吗？ A a c b A a A c a 课堂小结 请同学们说说这节课的收获 和体会！