中考数学一轮复习知识点+题型专题讲义12 一元二次方程（教师版）

中考数学一轮复习知识点+题型专题讲义12 一元二次方程（教师版）

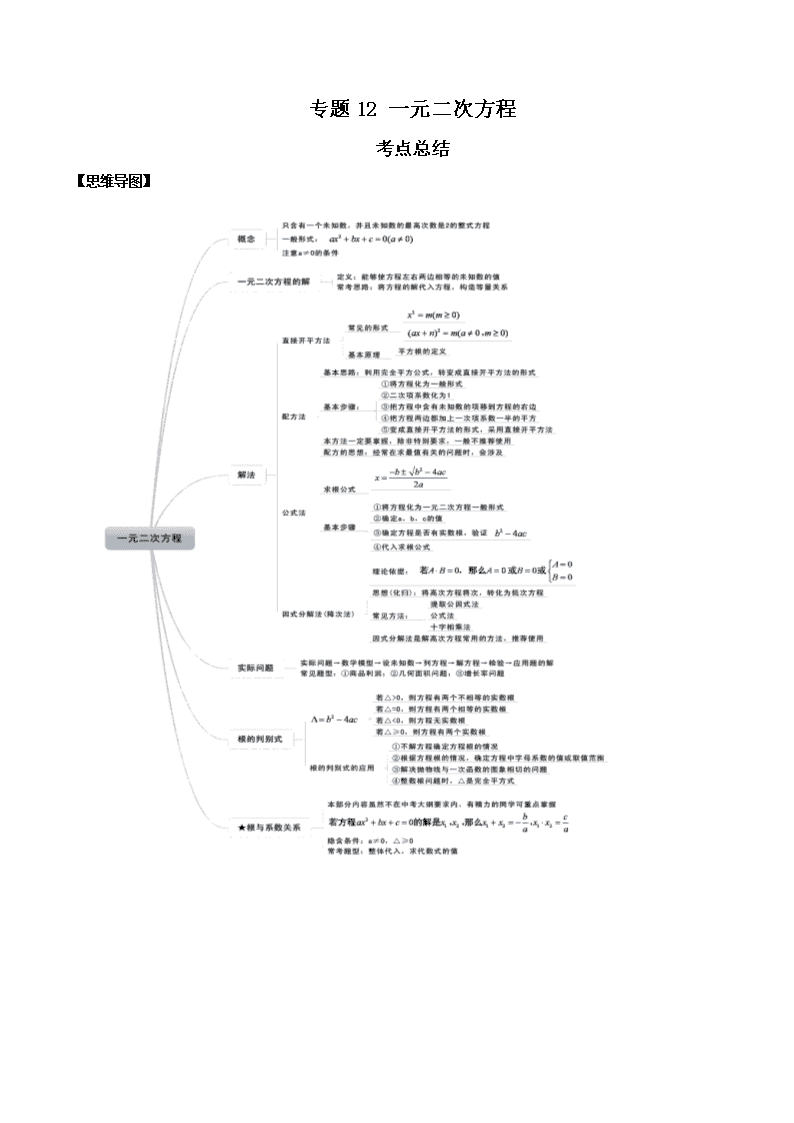
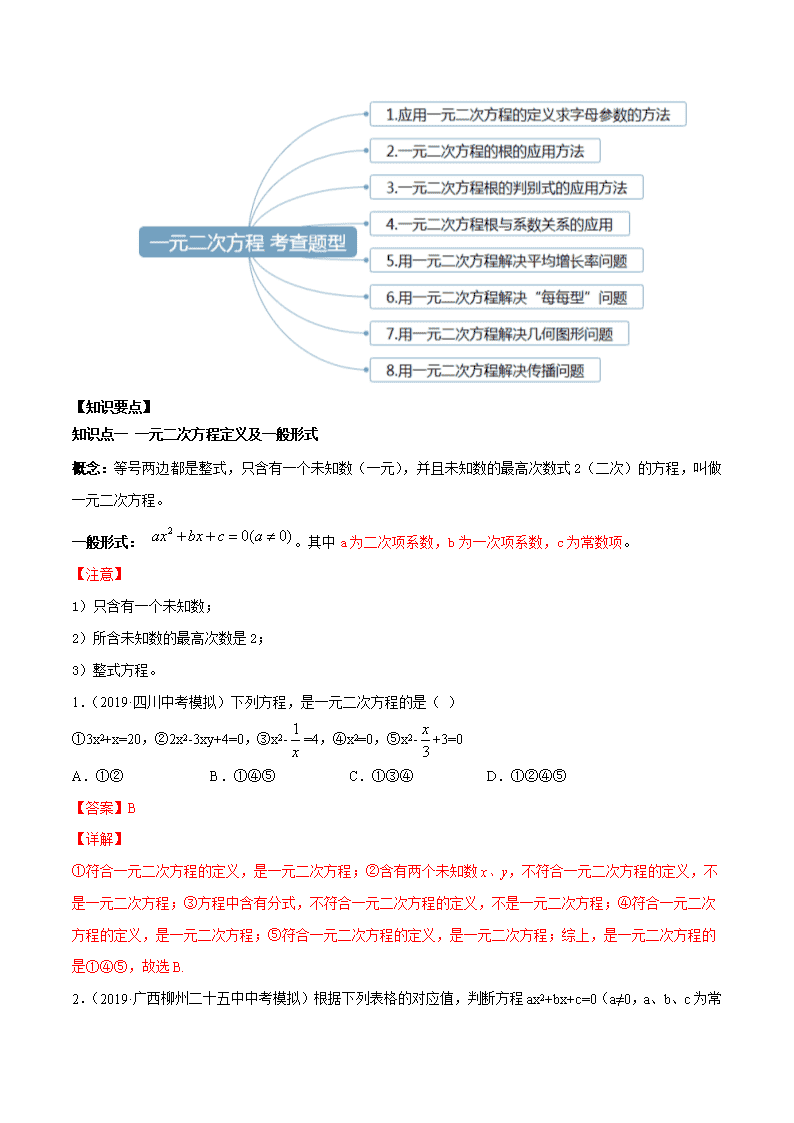
专题 12 一元二次方程 考点总结 【思维导图】 【知识要点】 知识点一 一元二次方程定义及一般形式 概念：等号两边都是整式，只含有一个未知数（一元），并且未知数的最高次数式 2（二次）的方程，叫做 一元二次方程。 一般形式： 2 0( 0)ax bx c a    。其中 a 为二次项系数，b 为一次项系数，c 为常数项。 【注意】 1）只含有一个未知数； 2）所含未知数的最高次数是 2； 3）整式方程。 1．（2019·四川中考模拟）下列方程，是一元二次方程的是（ ） ①3x2+x=20，②2x2-3xy+4=0，③x2- 1 x =4，④x2=0，⑤x2- 3 x +3=0 A．①② B．①④⑤ C．①③④ D．①②④⑤ 【答案】B 【详解】 ①符合一元二次方程的定义，是一元二次方程；②含有两个未知数 x、y，不符合一元二次方程的定义，不 是一元二次方程；③方程中含有分式，不符合一元二次方程的定义，不是一元二次方程；④符合一元二次 方程的定义，是一元二次方程；⑤符合一元二次方程的定义，是一元二次方程；综上，是一元二次方程的 是①④⑤，故选 B. 2．（2019·广西柳州二十五中中考模拟）根据下列表格的对应值，判断方程 ax2+bx+c=0（a≠0，a、b、c 为常 数）一个解的范围是（ ） x 3.23 3.24 3.25 3.26 ax2+bx+c ﹣0.06 ﹣0.02 0.03 0.09 A．3＜x＜3.23 B．3.23＜x＜3.24 C．3.24＜x＜3.25 D．3.25＜x＜3.26 【答案】C 【详解】 观察表格可知 ax2+bx+c 的值与 0 比较接近的是-0.02 和 0.03，相对应的 x 的值分别为 3.24 秘 3.25，因此方程 ax2+bx+c=0（a≠0，a、b、c 为常数）一个解的范围是 3.24＜x＜3.25； 故选 C. 3．（2019·广东中考模拟）方程 2x2﹣3x﹣5=0 的二次项系数、一次项系数、常数项分别为（ ） A．3、2、5 B．2、3、5 C．2、﹣3、﹣5 D．﹣2、3、5 【答案】C 【详解】2x2﹣3x﹣5=0 的二次项系数、一次项系数、常数项分别为 2、﹣3、﹣5. 故选 C. 4．（2018·湖南中考模拟）下列方程中是关于 x 的一元二次方程的是（ ） A． 2 2 1 0x x   B． 2 0ax bx c   C．  1 2 1x x   D． 2 23 2 5 0x xy y   【答案】C 【详解】 A. 是分式方程，故此选项错误； B. 当 a≠0 时，是一元二次方程，故此选项错误； C. 是一元二次方程，故此选项正确； D. 是二元二次方程，故此选项错误； 故选：C. 5．（2018·湖北中考模拟）下列关于 x 的方程中，属于一元二次方程的是（ ） A．x﹣1=0 B．x2+3x﹣5=0 C．x3+x=3 D．ax2+bx+c=0 【答案】B 【详解】 A. 未知数的最高次数不是 2 ，不是一元二次方程，故此选项错误； B. 是一元二次方程，故此选项正确； C. 未知数的最高次数是 3，不是一元二次方程，故此选项错误； D. a=0 时，不是一元二次方程，故此选项错误； 故选：B. 考查题型一 应用一元二次方程的定义求字母参数的方法 1．（2019·吉林中考模拟）若关于 x 的方程   2m 1 1 0x mx    是一元二次方程，则 m 的取值范围是 （ ） A． m 1 . B． m 1 . C． m 1 D．  m 0 . 【答案】A 【详解】 由题意得：m﹣1≠0， 解得：m≠1， 故选：A． 2．（2019·四川中考模拟）若   2 22 3aa x   是关于 x 的一元二次方程，则 a 的值是（ ） A．0 B．2 C．-2 D．±2 【答案】C 【详解】 由题意得： 2 2 2, 2 0a a    ，解得：a=-2.故选 C. 3．（2017·重庆中考模拟）若方程    2 11 1 2 0mm x m x     是一元二次方程，则 m 的值为（ ） A．0 B．±1 C．1 D．–1 【答案】D 【详解】 因为方程    2 11 1 2 0mm x m x     是一元二次方程, 所以 2 1 2m   ,   1 0m  , 解得 1m   且 1m  所以 1m   , 故选 D. 4．（2019·汕头市潮南区阳光实验学校中考模拟）关于 x 的一元二次方程（m﹣1）x2+5x+m2﹣3m+2＝0 的常 数项为 0，则 m 等于（ ） A．1 B．2 C．1 或 2 D．0 【答案】B 【详解】 根据一元二次方程的相关概念可知，m-1  0， 2 3 2 0m m   ，解得：m=2. 故选：B. 考查题型二 一元二次方程的根的应用方法 1．（2019·四川中考模拟）若 n（ 0n  ）是关于 x 的方程 2 2 0x mx n   的根，则 m+n 的值为（ ） A．1 B．2 C．-1 D．-2 【答案】D 【详解】 解：∵  n n 0 是关于 x 的方程 2x mx 2n 0   的根， ∴ 2n mn 2n 0   ，即 n(n+m+2)=0, ∵ n 0, ∴n+m+2=0,即 m+n=-2, 故选 D. 2．（2019·中山市杨仙逸中学中考模拟）已知 y＝0 是关于 y 的一元二次方程（m﹣1）y2+my+4m2﹣4＝0 的 一个根，那么 m 的值是（ ） A．0 B．±1 C．1 D．﹣1 【答案】D 【详解】 把 y=0 代入（m-1）y2+my+4m2-4=0 得： 4m2-4=0，即 m2-1=0 解得：m1=1，m2=-1 当 m=1 时，关于 y 的方程由于二次项系数为 0，不是一元二次方程， 所以 m=-1． 故选 D． 3．（2018·河北中考模拟）若关于 x 的一元二次方程 ax2+bx+6=0 的一个根为 x=﹣2，则代数式 6a﹣3b+6 的 值为（ ） A．9 B．3 C．0 D．﹣3 【答案】D 【详解】 ∵关于 x 的一元二次方程 2 6 0ax bx   的一个根为 x=−2， ∴    22 2 6 0a b       ， 化简，得 2a−b+3=0， ∴2a−b=−3， ∴6a−3b=−9， ∴6a−3b+6=−9+6=−3， 故选 D. 知识点 2：解一元二次方程（重点） 方法一：配方法（最基础的解法） 配方的过程需注意：若方程二次项系数为 1 时，“方程两边加一次项系数一半的平方” 用配方法解一元二次方程 2 0( 0)ax bx c a    的一般步骤  移项：使方程左边为二次项与一次项，右边为常数项；  二次项系数化为 1：方程两边都除以二次项系数；  配方：方程两边都加上一次项系数一般的平方，把方程化为 2( ) ( 0)x m n n   的形式； 【注意】：1）当 0n  时，方程无解 2）若方程二次项系数为 1 时，“方程两边加一次项系数一半的平方”  求解：判断右边等式符号，开平方并求解。 1．（2019·江苏中考真题）用配方法解方程 2 8 9 0x x   ，变形后的结果正确的是( ) A． 24 9x    B． 24 7x    C． 24 25x   D． 24 7x   【答案】D 【详解】 2 8 9 0x x   ， 2 8 9x x   ， 2 2 28 4 9 4x x     ， 所以  24 7x   ， 故选 D. 2.．（2018·浙江中考模拟）用配方法解一元二次方程 x2﹣6x﹣1=0 时，下列变形正确的是（ ） A．（x﹣3）2=1 B．（x﹣3）2=10 C．（x+3）2=1 D．（x+3）2=10 【答案】B 【详解】 x2﹣6x﹣1=0 方程移项得：x2-6x=1， 配方得：x2-6x+9=10，即（x-3）2=10， 故选：B． 3.．（2015·湖北中考真题）用配方法解一元二次方程 x2﹣6x﹣4=0，下列变形正确的是（ ） A．（x﹣6）2=﹣4+36 B．（x﹣6）2=4+36 C．（x﹣3）2=﹣4+9 D．（x﹣3）2=4+9 【答案】D 【详解】 x2﹣6x﹣4=0， x2﹣6x=4， x2﹣6x+9=4+9， （x﹣3）2=4+9， 故选 D. 方法二：直接开平方法（最基础的解法） 概念：形如 2( ) ( 0)x a b b   的方程可以用直接开平方法解，两边直接开平方得 x a b  或者 x a b   ，最后通过解两个一元一次方程得到原方程的解。 【注意】 1)若 b ≥ 0，方程有两个实数根。 （若 b > 0，方程有两个不相等的实数根；若 b = 0，方程有两个相等的实数根） 2)若 b<0，方程无解。 1．（2019·江苏中考模拟）一元二次方程 ( 1)( 3) 2 5x x x    根的情况是（ ） A．无实数根 B．有一个正根，一个负根 C．有两个正根，且都小于 3 D．有两个正根，且有一根大于 3 【答案】D 【详解】 （x+1）（x﹣3）=2x﹣5 整理得：x2﹣2x﹣3=2x﹣5，则 x2﹣4x+2=0，（x﹣2）2=2，解得：x1=2+ 2 ＞3，x2=2﹣ 2 ，故有两个正根， 且有一根大于 3． 故选 D． 2．（2019·四川中考模拟）对于两个实数 a ，b ，用  max ,a b 表示其中较大的数，则方程  max , 2 1x x x x    的解是（ ） A．1，1 2 B．1，1 2 C． 1 ，1 2 D． 1 ，1 2 【答案】C 【详解】 ∵max（a，b）表示其中较大的数， ∴当 x＞0 时，max（x，-x）=x， 方程为 x2=2x+1， x2-2x+1=2， （x-1）2=2， ∴x-1=± 2 ， ∴x=1± 2 ， ∴x＞0， ∴x=1+ 2 ； 当 x＜0 时，max（x，-x）=-x． 方程为-x2=2x+1 x2+2x+1=0， （x+1）2=0， ∴x=-1， 故方程 x×max（x，-x）=2x+1 的解是-1，1+ 2 故选 C． 3．（2018·福建中考模拟）设一元二次方程（ 1x  ）（ 3x  ）=m（m＞0）的两实数根分别为α、β且α＜β， 则α、β满足（ ） A．-1＜α＜β＜3 B．α＜-1 且β＞3 C．α＜-1＜β＜3 D．-1＜α＜3＜β 【答案】B 【详解】 x2-2x-3=m，（x－1）2=4+m，∴x－1=± 4 m ，x=1± 4 m ． ∵m＞0，∴ 4 m ＞2，∴α= 1－ 4 m ＜－1，β= 1+ 4 m ＞3，故α＜-1 且β＞3．故选 B． 方法三：公式法（常用解法） 一元二次方程 2 0( 0)ax bx c a    根的判别式： 2 4b ac    0  方程有两个不相等的实根: 2 4 2 b b acx a    （ 2 4 0b ac  ）  ( )f x 的图像与 x 轴有两 个交点  0  方程有两个相等的实根  ( )f x 的图像与 x 轴有一个交点  0  方程无实根  ( )f x 的图像与 x 轴没有交点 用公式法解一元二次方程 2 0( 0)ax bx c a    的一般步骤：  把方程化为一般形式，确定 a、b、c 的值(若系数是分数通常将其化为整数，方便计算);  求出 b2-4ac 的值，根据其值的情况确定一元二次方程是否有解;  如果 b2-4ac≥0, 将 a、b、c 的值代入求根公式： 2 4 2 b b acx a     最后求出 x1，x2 1．（2019·广西中考模拟）关于 x 的方程 2( 5) 4 1 0a x x    有实数根，则 a 满足（ ） A． 1a  B． 1a  且 5a  C． 1a  且 5a  D． 5a  【答案】A 【详解】 当 a=5 时，原方程变形为-4x-1=0，解得 x=- 1 4 ； 当 a≠5 时，△=（-4）2-4（a-5）×（-1）≥0，解得 a≥1，即 a≥1 且 a≠5 时，方程有两个实数根， 所以 a 的取值范围为 a≥1． 故选 A． 2．（2019·福建中考模拟）不解方程，判别方程 2x2﹣3 2 x＝3 的根的情况( ) A．有两个相等的实数根 B．有两个不相等的实数根 C．有一个实数根 D．无实数根 【答案】B 【详解】 一元二次方程的根的情况与根的判别式  有关， 2 4b ac   2( 3 2) 4 2 ( 3)      42 0  ，方程有两个不相等的实数根，故选 B 3．（2019·新疆中考模拟）已知关于 x 的一元二次方程 22 3 0x kx   有两个相等的实根，则 k 的值为（ ） A． 2 6 B． 6 C．2 或 3 D． 2 或 3 【答案】A 【详解】 ∵方程 22 3 0x kx   有两个相等的实根， ∴△=k2-4×2×3=k2-24=0， 解得：k= 2 6 ． 故选：A． 考查题型三 一元二次方程根的判别式的应用方法 1．（2019·河南中考模拟）关于 x 的一元二次方程（k﹣1）x2﹣2x+3＝0 有两个实数根，则 k 的取值范围是（ ） A．k≤ 4 3 且 k≠1 B．k≤ 4 3 C．k＜ 4 3 且 k≠1 D．k＜ 4 3 【答案】A 【详解】 解：根据题意得  1 0 4 4 3 0k k   ﹣ 且 ＝﹣ ﹣1 ，解得 4 3k  ， 所以 k 的范围为 4 13k k 且 ． 故选：A． 2．（2015·四川中考真题）方程 ݉ െ െ ݉ = 有两个实数根，则 ݉ 的取值范围（ ） A． ݉ > െ B． ݉ െ 且 ݉ െ C． ݉ ≥ D． ݉ 且 ݉ െ【答案】B 【详解】 解：根据题意得 ݉ െ ， ݉ ≥ ， = ݉ െ ݉ െ ≥ ， 解得 m≤ െ 且 m≠2． 故选 B． 3．（2019·安徽中考模拟）若关于 x 的一元二次方程 2 22( 1) 1 0x k x k     有实数根，则 k 的取值范围是 （ ） A．k≥1 B．k＞1 C．k＜1 D．k≤1 【答案】D 【详解】 ∵关于 x 的一元二次方程 x2+2（k﹣1）x+k2﹣1=0 有实数根， ∴△=b2﹣4ac=4（k﹣1）2﹣4（k2﹣1）=﹣8k+8≥0， 解得：k≤1． 故选：D． 4．（2018·广东中考模拟）关于 x 的一元二次方程 x2-2x-（m-1）=0 有两个不相等的实数根，则实数 m 的取 值范围是（ ） A． 0m  且 1m  B． 0m  C． 0m  且 1m  D． 0m  【答案】A 【详解】 ∵关于 x 的一元二次方程 x2﹣2x﹣（m﹣1）=0 有两个不相等的实数根，∴△=（﹣2）2﹣4×1×[﹣（m﹣1）]=4m ＞0，∴m＞0． 故选 B． 5．（2019·湖北中考模拟）关于 x 的一元二次方程 2 3 0x x m   有两个不相等的实数根，则实数 m 的取值 范围是 ( ) A． 9 4m  B． 9 4m„ C． 9 4m  D． 9 4m… 【答案】A 【详解】 ∵关于 x 的一元二次方程 x2﹣3x+m=0 有两个不相等的实数根， ∴△=b2﹣4ac=（﹣3）2﹣4×1×m＞0， ∴m＜ 9 4 ， 故选 A． 方法四：因式分解法（仔细观察方程，灵活使用） 用因式分解一元二次方程 2 0( 0)ax bx c a    的一般步骤：  将方程右边得各项移到方程左边，使方程右边为 0；  将方程左边分解为两个一次因式相乘的形式；  令每个因式分别为零，得到两个一元一次方程；  求解 归纳：右化零，左分解，两因式，各求解 1．（2019·湖州市南浔区南浔锦绣实验学校中考模拟）若 x＝－2 是关于 x 的一元二次方程 x2＋ 3 2 ax－a2＝0 的一个根，则 a 的值为（ ） A．－1 或 4 B．－1 或－4 C．1 或－4 D．1 或 4 【答案】C 【详解】 ∵x=-2 是关于 x 的一元二次方程 2 23 02x ax a   的一个根， ∴（-2）2+ 3 2 a×（-2）-a2=0，即 a2+3a-4=0， 整理，得（a+4）（a-1）=0， 解得 a1=-4，a2=1． 即 a 的值是 1 或-4． 故选 A． 2．（2019·长沙市南雅中学中考模拟）三角形两边长分别为 4 和 6，第三边是方程 x2﹣13x+36＝0 的根，则三 角形的周长为（ ） A．14 B．18 C．19 D．14 或 19 【答案】D 【详解】 解：（x﹣4）（x﹣9）＝0， x﹣4＝0 或 x﹣9＝0， 所以 x1＝4，x2＝9， 即三角形的第三边长为 4 或 9， 所以三角形的周长为 4+6+4＝14 或 4+6+9＝19． 故选：D． 3．（2013·宁夏中考真题）一元二次方程  x x 2 2 x   的根是 A．﹣1 B．2 C．1 和 2 D．﹣1 和 2 【答案】D 【详解】  x x 2 2 x       x x 2 x 2 0       x 2 x 1 0    x 2 0 x 1 0    或 1 2x 2 x 1  ， , 故选 D. 4．（2018·四川中考模拟）已知一元二次方程 x2-8x+15=0 的两个解恰好分别是等腰△ABC 的底边长和腰长， 则△ABC 的周长为（ ） A．13 B．11 或 13 C．11 D．12 【答案】B 【详解】 x2-8x+15=0， 分解因式得：（x-3）（x-5）=0， 可得 x-3=0 或 x-5=0， 解得：x1=3，x2=5， 若 3 为底边，5 为腰时，三边长分别为 3，5，5，周长为 3+5+5=13； 若 3 为腰，5 为底边时，三边长分别为 3，3，5，周长为 3+3+5=11， 综上，△ABC 的周长为 11 或 13． 故选 B. 方法五：韦达定理（根与系数关系） 我们将一元二次方程化成一般式 ax2+bx+c＝0（a ， ≥ ）之后，设它的两个根是 1x 和 2x ，则 1x 和 2x 与 方程的系数 a，b，c 之间有如下关系： 1x + 2x ＝ b a  ； 1x  2x ＝ c a 考查题型四 一元二次方程根与系数关系的应用 1．（2017·湖北中考模拟）已知 mn≠1，且 5m2+2010m+9=0，9n2+2010n+5=0，则 m n 的值为（ ） A．﹣402 B． 5 9 C． 9 5 D． 670 3 【答案】C 【详解】 将 9n2+2010n+5=0 方程两边同除以 n2，变形得：5×（ 1 n ）2+2010× 1 n +9=0，,又 5m2+2010m+9=0， ∴m 与 1 n 为方程 5x2+2010x+9=0 的两个解，则根据一元二次方程的根与系数的关系可得 m• 1 n = m n = 9 5 ． 故选：C 2．（2019·贵州中考真题）一元二次方程 x2﹣3x+1＝0 的两个根为 x1，x2，则 x12+3x2+x1x2﹣2 的值是（ ） A．10 B．9 C．8 D．7 【答案】D 【详解】 ∵x1 为一元二次方程 x2﹣3x+1＝0 的根， ∴x12﹣3x1+1＝0， ∴x12＝3x1﹣1， ∴x12+3x2+x1x2﹣2＝3x1﹣1+3x2+x1x2﹣2＝3（x1+x2）+x1x2﹣3， 根据题意得 x1+x2＝3，x1x2＝1， ∴x12+3x2+x1x2﹣2＝3×3+1﹣3＝7． 故选：D． 3．（2017·广东中考模拟）关于的方程 2 2 0x ax a   的两根的平方和是 5，则 a 的值是( ) A．-1 或 5 B．1 C．5 D．-1 【答案】D 【详解】 设方程的两根为 1x 、 2x ，则 1 2x x a  ， 1 2 2x x a  ，  2 2 21 5x x  ，   2 1 2 1 22 5x x x x    ，  2 4 5 0a a   ，  1 5a  ， 2 1a   ，  2 8 0a a   ，  1a   . 故选： D . 4.（2019·湖北中考真题）关于 x 的一元二次方程 2 4 0x x m   的两实数根分别为 1x 、 2x ，且 1 23 5x x  ， 则 m 的值为（ ） A． 7 4 B． 7 5 C． 7 6 D．0 【答案】A 【详解】 解：∵x1+x2=4， ∴x1+3x2=x1+x2+2x2=4+2x2=5， ∴x2= 1 2 ， 把 x2= 1 2 代入 x2-4x+m=0 得：（ 1 2 ）2-4× 1 2 +m=0， 解得：m= 7 4 ， 故选：A． 5．（2019·广州市第六十五中学中考模拟）已知 a、b 为一元二次方程 2 2 9 0x x   的两个根，那么 2a a b  的值为（ ） A．-7 B．0 C．7 D．11 【答案】D 【详解】 解：由题意得： 2 2 9 0a a   ，则 2 9a a a   ，    2 9 9 9 2 11a a b a b a b            ， 故选择 D. 知识点 4： 一元二次方程的应用 列一元二次方程解应用题，其步骤和二元一次方程组解应用题类似：  “审”，弄清楚已知量，未知量以及他们之间的等量关系；  “设”指设元，即设未知数，可分为直接设元和间接设元；  “列”指列方程，找出题目中的等量关系，再根据这个关系列出含有未知数的等式，即方程。  “解”就是求出说列方程的解；  “答”就是书写答案，检验得出的方程解，舍去不符合实际意义的方程。 注意：一元二次方程考点：定义的考察；解方程及一元二次方程的应用。 考查题型五 用一元二次方程解决平均增长率问题 1．（2018·河南中考模拟）某种品牌运动服经过两次降价，每件零售价由 560 元降为 315 元，已知两次降价 的百分率相同，求每次降价的百分率．设每次降价的百分率为 x，下面所列的方程中正确的是（ ） A．560（1＋x）2＝315 B．560（1－x）2＝315 C．560（1－2x）2＝315 D．560（1－x2）＝315 【答案】B 【详解】 试题分析：根据题意，设设每次降价的百分率为 x，可列方程为 560（1-x）²=315. 故选：B 2．（2013·甘肃中考真题）某超市一月份的营业额为 36 万元，三月份的营业额为 48 万元，设每月的平均增 长率为 x，则可列方程为（ ） A．48（1﹣x）2=36 B．48（1+x）2=36 C．36（1﹣x）2=48 D．36（1+x）2=48 【答案】D 【详解】 ∵某超市一月份的营业额为 36 万元，每月的平均增长率为 x， ∴二月份的营业额为 36（1+x），三月份的营业额为 36（1+x）×（1+x）=36（1+x）2. ∴根据三月份的营业额为 48 万元，可列方程为 36（1+x）2=48. 故选 D. 3．（2018·安徽中考模拟）某企业因春节放假，二月份产值比一月份下降 20% ，春节后生产呈现良好上升势 头，四月份比一月份增长15% ，设三、四月份的月平均增长率为 x，则下列方程正确的是 ( ) A．   2 1 20% 1 1 15%x    B．  21 15% (1 ) 1 20%x    C．   2 1 15% 1 1 20%x    D．  21 20% (1 ) 1 15%x    【答案】D 【详解】 设一月份的产量为 a，由题意可得，    2a 1 20% (1 x) a 1 15%    ， 则  21 20% (1 x) 1 15%    ， 故选 D． 考查题型六 用一元二次方程解决“每每型”问题 1．（2018·海南中考模拟）某商场销售一批名牌衬衫，平均每天可售出 20 件，每件盈利 40 元，为扩大销售， 尽快减少库存，商场决定釆取降价措施，调查发现，每件衬衫，每降价 1 元，平均每天可多销售 2 件，若 商场每天要盈利 1200 元，每件衬衫应降价（ ） A．5 元 B．10 元 C．20 元 D．10 元或 20 元 【答案】C 【详解】 设每件衬衫应降价 x 元，则每天可销售（20+2x）件， 根据题意得：（40-x）（20+2x）=1200， 解得：x1=10，x2=20． ∵扩大销售，减少库存， ∴x=20． 故选 C． 2．（2019·忻城县民族中学中考模拟）宾馆有 50 间房供游客居住，当每间房每天定价为 180 元时，宾馆会住 满；当每间房每天的定价每增加 10 元时，就会空闲一间房.如果有游客居住，宾馆需对居住的每间房每天支 出 20 元的费用.当房价定为 x 元时，宾馆当天的利润为 10890 元.则有( ) A． (180 20) 50 1089010 xx        B． 18050 50 20 1089010 xx        C． 180( 20) 50 1089010 xx       D． ( 180) 50 50 20 1089010 xx         【答案】C 【详解】 房价定为 x 元，由题意得   x 180x 20 50 1089010       ， 故选 C. 3.（2019·山东中考模拟）一商店销售某种商品，平均每天可售出 20 件，每件盈利 40 元.为了扩大销售、增 加盈利，该店采取了降价措施，在每件盈利不少于 25 元的前提下，经过一段时间销售，发现销售单价每降 低 1 元，平均每天可多售出 2 件. （1）若降价 3 元，则平均每天销售数量为________件； （2）当每件商品降价多少元时，该商店每天销售利润为 1200 元？ 【答案】（1）26；（2）每件商品降价 10 元时，该商店每天销售利润为 1200 元. 【详解】 （1）若降价 3 元，则平均每天销售数量为 20+2×3=26 件． （2）设每件商品应降价 x 元时，该商店每天销售利润为 1200 元． 根据题意，得 （40-x）（20+2x）=1200， 整理，得 x2-30x+200=0， 解得：x1=10，x2=20． ∵要求每件盈利不少于 25 元， ∴x2=20 应舍去， ∴x=10． 答：每件商品应降价 10 元时，该商店每天销售利润为 1200 元． 考查题型七 用一元二次方程解决几何图形问题 1．（2019·广西中考模拟）如图，有一张矩形纸片，长 10cm，宽 6cm，在它的四角各减去一个同样的小正方 形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是 32cm2，求剪去的小正方形 的边长．设剪去的小正方形边长是 xcm，根据题意可列方程为（ ） A．10×6﹣4×6x=32 B．（10﹣2x）（6﹣2x）=32 C．（10﹣x）（6﹣x）=32 D．10×6﹣4x2=32 【答案】B 【详解】 设剪去的小正方形边长是 xcm，则纸盒底面的长为（10−2x）cm，宽为（6−2x）cm， 根据题意得：（10−2x）（6−2x）＝32． 故选：B． 2（2019·广西中考真题）扬帆中学有一块长30m，宽 20m 的矩形空地，计划在这块空地上划出四分之一的 区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 xm，则可列方程为（ ） A．   330 20 20 304x x     B．   130 2 20 20 304x x     C． 130 2 20 20 304x x     D．   330 2 20 20 304x x     【答案】D 【详解】 设花带的宽度为 xm，则可列方程为 3(30 2 )(20 ) 20 304x x     ， 故选：D． 3．（2012·广东中考模拟）在一幅长80cm ，宽 50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂 图，如图所示，如果要使整幅挂图的面积是 25400cm ，设金色纸边的宽为 xcm ，那么 x 满足的方程是（ ） A． 2 130 1400 0x x   B． 2 65 350 0x x   C． 2 130 1400 0x x   D． 2 65 350 0x x   【答案】B 【详解】 由题意，设金色纸边的宽为 xcm ， 得出方程：（80+2x）（50+2x）=5400， 整理后得： 2 65 350 0x x   故选：B. 4．（2019·安徽中考模拟）如图，某小区计划在一块长为 32m，宽为 20m 的矩形空地上修建三条同样宽的道 路，剩余的空地上种植草坪．若草坪的面积为 570m2，道路的宽为 xm，则可列方程为（ ） A．32×20﹣2x2＝570 B．32×20﹣3x2＝570 C．（32﹣x）（20﹣2x）＝570 D．（32﹣2x）（20﹣x）＝570 【答案】D 【详解】 解：设道路的宽为 xm，根据题意得：（32-2x）（20-x）=570， 故选：D． 考查题型八 用一元二次方程解决传播问题 1．（2019·黑龙江中考真题）某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的 支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是 43，则这种植物每个支干长出的 小分支个数是（ ） A． 4 B．5 C． 6 D． 7 【答案】C 【详解】 设这种植物每个支干长出 x 个小分支， 依题意，得： 21 43x x   ， 解得： 1 7x   （舍去）， 2 6x  ． 故选：C． 2．（2018·安徽中考模拟）某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送 1035 张照片，如果全班有 x 名同学，根据题意，列出方程为（ ） A．x(x+1)=1035 B．x(x-1)=1035 C． 1 2 x(x+1)=1035 D． 1 2 x(x-1)=1035 【答案】B 【详解】 如果全班有 x 名同学，那么每名同学要送出（x-1）张，共有 x 名学生，那么总共送的张数应该是 x（x-1） 张，即可列出方程． ∵全班有 x 名同学， ∴每名同学要送出（x-1）张； 又∵是互送照片， ∴总共送的张数应该是 x（x-1）=1035． 故选 B 3．（2019·天津中考模拟）某校羽毛球队有若干名队员，任意两名队员之间进行一场友谊赛，共进行了 36 场比赛.如果全队有 x 名队员，根据题意下列方程正确的是（ ） A． ( 1) 36x x   B． ( 1) 36x x   C． ( 1) 362 x x   D． ( 1) 362 x x   【答案】C 【详解】 解：设有 x 名队员，每个队员都要赛（x-1）场，但两人之间只有一场比赛， 故 1 ( 1) 362 x x   ， 故选：C．