- 2023-06-22 发布 |
- 37.5 KB |
- 79页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
工学数字电子技术基础时序逻辑电路
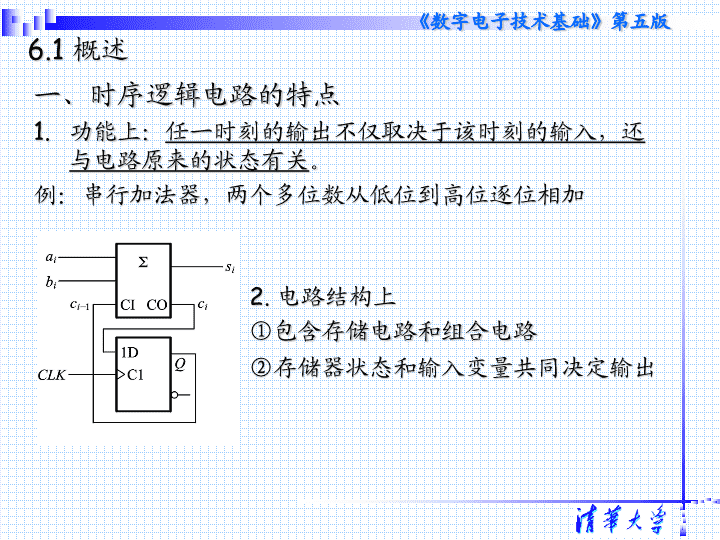
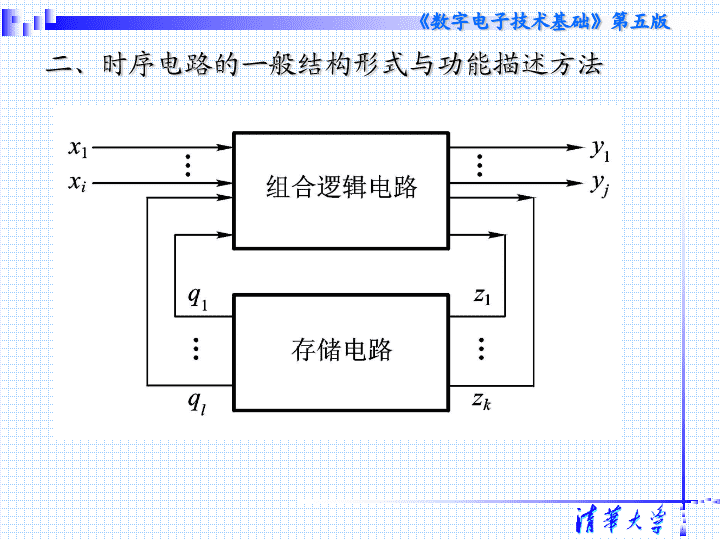
第六章 时序逻辑电路 6.1 概述 一、时序逻辑电路的特点 功能上: 任一时刻的输出不仅取决于该时刻的输入,还与电路原来的状态有关 。 例:串行加法器,两个多位数从低位到高位逐位相加 2. 电路结构上 ①包含存储电路和组合电路 ②存储器状态和输入变量共同决定输出 二、时序电路的一般结构形式与功能描述方法 可以用三个方程组来描述: 三、时序电路的分类 1. 同步时序电路与异步时序电路 同步:存储电路中所有触发器的时钟使用统一的 clk, 状态变化发生在同一时刻 异步:没有统一的 clk, 触发器状态的变化有先有后 2. Mealy 型和 Moore 型 Mealy 型: Moore 型: 6.2 时序电路的分析方法 6.2.1 同步时序电路的分析方法 分析:找出给定时序电路的逻辑功能 即找出在输入和 CLK 作用下,电路的次态和输出。 一般步骤: ①从给定电路写出存储电路中每个触发器的驱动方程 (输入的逻辑式),得到整个电路的 驱动方程。 ②将驱动方程代入触发器的特性方程,得到 状态方程。 ③从给定电路写出 输出方程。 例: TTL 电路 6.2.2 时序电路的状态转换表、状态转换图、状态机流程图和时序图 一、状态转换表 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 0 0 0 0 0 1 1 1 1 1 0 0 0 0 二、状态转换图 三、状态机流程图( State Machine Chart ) 四、时序图 例: ( 4 )列状态转换表: ( 5 )状态转换图 00 01 10 11 0 01/0 10/0 11/0 00/1 1 11/1 00/0 01/0 10/0 *6.2.3 异步时序逻辑电路的分析方法 各触发器的时钟不同时发生 例: TTL 电路 C1 1J 1K C1 1J 1K C1 1J 1K FF 0 FF 1 FF 2 Q 0 Q 1 Q 2 Y CP 1 1 [ 例 ] 试分析图示电路的逻辑功能,并画出状态转换图 和时序图。 这是异步时序逻辑电路。分析如下: 解: C1 C1 FF 1 和 FF 2 受 Q 0 下降沿触发 CP C1 FF 0 受 CP 下降沿触发 C1 1J 1K C1 1J 1K C1 1J 1K FF 0 FF 1 FF 2 Q 0 Q 1 Q 2 Y CP 1 1. 写方程式 ( 1 ) 时钟方程 ( 3 ) 驱动方程 ( 2 ) 输出方程 ( 4 ) 状态方程 CP 1 = CP 2 = Q 0 FF 1 、 FF 2 由 Q 0 下降沿触发 CP 0 = CP FF 0 由 CP 下降沿触发 Y = Q 2 n 1 1J 1K J 0 = K 0 = 1 Q 2 n Q 1 n Q 1 n Q 2 Y 1K 1J J 2 = Q 1 n , K 2 = Q 1 n J 1 = Q 2 n , K 1 = 1 1J 1K 1 J 1 = Q 2 n , K 1 = 1 1. 写方程式 ( 1 ) 时钟方程 ( 3 ) 驱动方程 ( 2 ) 输出方程 ( 4 ) 状态方程 CP 1 = CP 2 = Q 0 FF 1 和 FF 2 由 Q 0 下降沿触发 CP 0 = CP FF 0 由 CP 下降沿触发 Y = Q 2 n J 0 = K 0 = 1 J 2 = Q 1 n , K 2 = Q 1 n Q 0 n +1 = J 0 Q 0 n + K 0 Q 0 n Q 1 n +1 = J 1 Q 1 n + K 1 Q 1 n Q 2 n +1 = J 2 Q 2 n + K 2 Q 2 n = 1 Q 0 n + 1 Q 0 n = Q 0 n 代入 J 0 = 1 , K 0 = 1 代入 J 1 = Q 2 n , K 1 = 1 Q 1 n +1 = Q 2 n Q 1 n Q 0 下降沿有效 Q 0 n +1 = Q 0 n CP 下降沿有效 Q 2 n +1 = Q 1 n Q 2 n +Q 1 n Q 2 n Q 0 下降沿有效 代入 J 2 = Q 1 n , K 2 = Q 1 n = Q 2 n Q 1 n + 1 Q 1 n = Q 2 n Q 1 n = Q 1 n Q 2 n + Q 1 n Q 2 n = Q 1 n Q 2 n +Q 1 n Q 2 n 2. 列状态转换真值表 设初始状态为 Q 2 Q 1 Q 0 = 000 0 1 0 0 0 0 0 Q 0 n +1 = Q 0 n = 0 = 1 Y = Q 2 n = 0 0 1 Y Q 0 n +1 Q 1 n +1 Q 2 n +1 Q 0 n Q 1 n Q 2 n 输 出 次 态 现 态 CP 2 CP 0 CP 1 时 钟 脉 冲 CP 0 = CP , FF 0 满足 时钟触发条件。 CP 1 = CP 2 = Q 0 为上升沿, FF 1 和 FF 2 不满足时钟触发 条件,其状态保持不变。 0 0 2. 列状态转换真值表 设初始状态为 Q 2 Q 1 Q 0 = 000 0 1 0 0 0 0 0 Y Q 0 n +1 Q 1 n +1 Q 2 n +1 Q 0 n Q 1 n Q 2 n 输 出 次 态 现 态 CP 2 CP 0 CP 1 时 钟 脉 冲 0 1 0 1 0 0 1 Q 0 n +1 = Q 0 n = 1 = 0 将新状态 “ 001 ” 作为现态,再计算下一个次态。 CP 1 = CP 2 = Q 0 为下降沿, FF 1 和 FF 2 满足时钟触发条件。 Q 2 n +1 = Q 1 n · Q 2 n + Q 1 n · Q 2 n = 0 · 0 +0 · 0 = 0 Y = Q 2 n = 0 Q 1 n +1 = Q 2 n · Q 1 n = 1·1 = 1 电路构成异步六进制计数器,同时向高位送出一个负跃变的进位信号。 3. 逻辑功能说明 2. 列状态转换真值表 设初始状态为 Q 2 Q 1 Q 0 = 000 0 1 0 0 0 0 0 Y Q 0 n +1 Q 1 n +1 Q 2 n +1 Q 0 n Q 1 n Q 2 n 输 出 次 态 现 态 CP 2 CP 0 CP 1 时 钟 脉 冲 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1 0 0 1 0 1 0 0 0 1 0 1 一直计算到电路状态进入循环为止。 依次类推 4. 画状态转换图和时序图 Q 2 Q 1 Q 0 x / y / 0 000 001 010 011 100 / 0 / 0 / 0 / 1 / 1 101 0 0 0 0 1 0 0 0 0 0 1 1 1 0 1 0 0 1 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 Y Q 0 n +1 Q 1 n +1 Q 2 n +1 Q 0 n Q 1 n Q 2 n 输 出 次 态 现 态 CP 2 CP 0 CP 1 时 钟 脉 冲 1 0 1 1 0 1 1 0 0 1 0 Y 1 1 0 0 1 0 1 0 0 Q 0 Q 1 Q 2 0 0 0 0 0 0 0 0 0 当计数至第 6 个计数脉冲 CP 时,电路状态进入循环, Y 输出进位脉冲下降沿。 CP 1 2 3 4 5 6 0 0 1 / 0 4. 画状态转换图和时序图 000 001 010 011 100 Q 2 Q 1 Q 0 x / y / 0 / 0 / 0 / 1 / 1 101 1 0 1 6.3 若干常用的时序逻辑电路 6.3.1 寄存器和移位寄存器 一、寄存器 ① 用于寄存一组二值代码, N 位寄存器由 N 个触发器组成,可存放一组 N 位二值代码。 ②只要求其中每个触发器可置 1 ,置 0 。 例 1 : 例:用维 - 阻触发器结构的 74HC175 二、移位寄存器(代码在寄存器中左 / 右移动) 具有存储 + 移位功能 器件实例: 74LS 194A , 左 / 右移,并行输入,保持,异步置零等 功能 R’ D S 1 S 0 工作状态 0 X X 置零 1 0 0 保持 1 0 1 右移 1 1 0 左移 1 1 1 并行输入 扩展应用( 4 位 8 位) 6.3.2 计数器 用于计数、分频、定时、产生节拍脉冲等 分类:按时钟分,同步、异步 按计数过程中数字增减分,加、减和可逆 按计数器中的数字编码分,二进制、二 - 十进制和 循环码 … 按计数容量分,十进制,六十进制 … 一、同步计数器 同步二进制计数器 ①同步二进制加法计数器 原理:根据二进制加法运算规则可知:在多位二进制数末位加 1 ,若第 i 位以下皆为 1 时,则第 i 位应翻转。 由此得出规律,若用 T 触发器构成计数器,则第 i 位触发器输入端 Ti 的逻辑式应为: 器件实例: 74161 工作状态 X 0 X X X 置 0 (异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括 C ) X 1 1 X 0 保持( C=0 ) 1 1 1 1 计数 ② 同步二进制减法计数器 原理:根据二进制减法运算规则可知:在多位二进制数末位减 1 ,若第 i 位以下皆为 0 时,则第 i 位应翻转。 由此得出规律,若用 T 触发器构成计数器,则第 i 位触发器输入端 Ti 的逻辑式应为: ③ 同步加减计数器 加 / 减 计数器 加 / 减 计数结果 加 / 减 计数器 计数结果 两种解决方案 a. 单时钟方式 加 / 减脉冲用同一输入端, 由加 / 减控制线的高低电平决定加 / 减 器件实例: 74LS191 (用 T 触发器) 工作状态 X 1 1 X 保持 X X 0 X 预置数 ( 异步 ) 0 1 0 加计数 0 1 1 减计数 b. 双时钟方式 器件实例: 74LS193 (采用 T’ 触发器,即 T=1 ) 2. 同步十进制计数器 ①加法计数器 基本原理:在四位二进制计数器基础上修改,当计到 1001 时,则下一个 CLK 电路状态回到 0000 。 能自启动 器件实例: 74 160 工作状态 X 0 X X X 置 0 (异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括 C ) X 1 1 X 0 保持( C=0 ) 1 1 1 1 计数 ② 减法计数器 基本原理:对二进制减法计数器进行修改,在 0000 时减 “ 1 ” 后跳变为 1001 ,然后按二进制减法计数就行了。 能自启动 ③ 十进制可逆计数器 基本原理一致,电路只用到 0000~1001 的十个状态 实例器件 单时钟: 74190,168 双时钟: 74192 二 . 异步计数器 1. 二进制计数器 ①异步二进制加法计数器 在末位 +1 时,从低位到高位逐位进位方式工作。 原则:每 1 位从 “ 1 ” 变 “ 0 ” 时,向高位发出进位,使高位翻转 ② 异步二进制减法计数器 在末位 -1 时,从低位到高位逐位借位方式工作。 原则:每 1 位从 “ 0 ” 变 “ 1 ” 时,向高位发出进位,使高位翻转 2 、异步十进制加法计数器 原理: 在 4 位二进制异步加法计数器上修改而成, 要跳过 1010 ~ 1111 这六个状态 1 2 3 4 5 6 7 8 9 10 J=0 J=1 J=0 J=K=1 J=1 J=0 器件实例:二-五- 十进制 异步计数器 74LS290 三、任意进制计数器的构成方法 用已有的 N 进制芯片,组成 M 进制计数器,是常用的方法。 N 进制 M 进制 1. N > M 原理:计数循环过程中设法跳过 N - M 个状态。 具体方法:置零法 置数法 例:将十进制的 74160 接成六进制计数器 异步置零法 工作状态 X 0 X X X 置 0 (异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括 C ) X 1 1 X 0 保持( C=0 ) 1 1 1 1 计数 例:将十进制的 74160 接成六进制计数器 异步置零法 置数法 (a) 置入0000 (b) 置入1001 2. N < M ① M=N1 × N2 先用前面的方法分别接成 N1 和 N2 两个计数器。 N1 和 N2 间的连接有两种方式: a. 并行进位方式:用同一个 CLK ,低位片的进位输出作为高位片的计数控制信号(如 74160 的 EP 和 ET ) b. 串行进位方式:低位片的进位输出作为高位片的 CLK ,两片始终同时处于计数状态 例:用 74160 接成一百进制 工作状态 X 0 X X X 置 0 (异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括 C ) X 1 1 X 0 保持( C=0 ) 1 1 1 1 计数 例:用两片 74160 接成一百进制计数器 并行进位法 串行进位法 ② M 不可分解 采用整体置零和整体置数法: 先用两片 接成 M’> M 的计数器 然后再采用置零或置数的方法 例:用 74160 接成二十九进制 工作状态 X 0 X X X 置 0 (异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括 C ) X 1 1 X 0 保持( C=0 ) 1 1 1 1 计数 例:用 74160 接成二十九进制 整体置零 (异步) 整体置数 (同步) [ 例 ] 由两片 CT74LS161 级联组成的四十二进制计数器。 CP CO D 0 CT T CT P CR LD D 1 D 2 D 3 Q 0 Q 1 Q 2 Q 3 1 CT74LS161 1 × × × × CO D 0 CT T CT P CR LD D 1 D 2 D 3 Q 0 Q 1 Q 2 Q 3 1 CT74LS161 & × × × × 计数 输入 十进制数 42 对应的二进制数为“ 00101010” ,当计数器计到 42 时,计数器的状态为 Q 3 Q 2 Q 1 Q 0 Q 3 Q 2 Q 1 Q 0 = 00101010 ,其反馈归零函数为 CR = Q 1 Q 3 Q 1 ,这时,与非门输出低电平 0 ,使两片 CT74LS161 同时被清零,从而实现了四十二进制计数。 四、移位寄存器型计数器 1. 环形计数器 2. 扭环形计数器 五、计数器应用实例 例 1 ,计数器 + 译码器 →顺序节拍脉冲发生器 例 2 ,计数器 + 数据选择器 →序列脉冲发生器 发生的序列: 00010111 6.4 时序逻辑电路的设计方法 6.4.1 同步时序逻辑电路的设计方法 设计的一般步骤 一、逻辑抽象,求出状态转换图或状态转换表 1. 确定输入 / 输出变量、电路状态数。 2. 定义输入 / 输出逻辑状态以及每个电路状态的含意,并对电路状态进行编号。 3. 按设计要求列出状态转换表,或画出状态转换图。 二、状态化简 若两个状态在相同的输入下有相同的输出,并转换到同一个次态,则称为等价状态;等价状态可以合并。 三、状态分配(编码) 1. 确定触发器数目。 2. 给每个状态规定一个代码。 (通常编码的取法、排列顺序都依照一定的规律) 四、选定触发器类型 求出状态方程,驱动方程,输出方程。 五、画出逻辑图 六、检查自启动 6.5.2 同步时序逻辑电路设计举例 [ 例 1 ] 设计一个递增同步六进制计数器,要求计数器状态转换代码具有相邻性(相邻的两组代码中只有一位代码不同),且代码不包含全 0 和全 1 的码组。 解:设计步骤 S 0 S 1 S 2 / 0 / 0 S 3 / 0 S 4 / 0 / 1 ( 1 ) 根据设计要求,画原始状态转换图。 根据题意可知该同步计数器的原始状态有 6 个,分别用 S 0 、 S 1 、 、 S 5 表示; S 0 为初始状态,在输入时钟脉冲 CP 作用下,电路状态依次转换。在状态为 S 5 时,输出 Y = 1 ,为其它状态时, Y = 0 。如再输入一个时钟脉冲 CP ,计数器返回初始状态,同时 Y 输出一个负跃变的进位信号。由此可画出下图所示的原始状态转换图。 S 5 / 0 ( 2 ) 列出状态转换编码表。 将电路状态用二进制码进行编码,通常采用自然二进制码。采用的码位数 n 与电路状态数 N 之间应满足 2 n ≥ N > 2 n -1 由于电路有 6 个状态,因此,该计数器由 3 个触发器构成,其状态为 3 位二进制编码,且不能选用 000 和 111 。设编码从 Q 0 n Q 1 n Q 0 n =001 开始,由此可列出电路状态转换编码表如下: 0 1 0 1 0 0 1 S 4 0 0 0 1 0 1 1 S 3 0 0 1 1 0 1 0 S 2 0 0 1 0 1 1 0 S 1 0 1 1 0 1 0 0 S 0 Y Q 0 n +1 Q 1 n +1 Q 2 n +1 Q 0 n Q 1 n Q 2 n 输出 次 态 现 态 状态顺序 1 1 0 0 1 0 1 S 5 4 3 2 1 0 等效十 5 进制数 ( 3 ) 确定触发器类型,求输出方程、状态 方程和驱动方程。 选用 JK 触发器。其特性方程为 Q n +1 = J Q n + K Q n 。 1 1 10 Q 2 n Q 1 n Q 0 n 0 1 00 01 11 1 × 1 0 0 × Q 2 n Q 1 n Q 0 n 0 1 00 01 11 0 × 0 1 1 × 0 10 10 Q 2 n Q 1 n Q 0 n 0 1 00 01 11 0 × 1 0 1 × 1 0 10 Q 2 n Q 1 n Q 0 n 0 1 00 01 11 0 × 0 0 0 × 1 0 Q 2 n +1 卡 诺 图 Q 1 n +1 卡 诺 图 Q 0 n +1 卡 诺 图 Y 卡 诺 图 0 输出方程为 状态方程为 将状态方程与 JK 触发器的特性方程 Q n +1 = J Q n + K Q n 进行比较,可得驱动方程为 , , , 0 1 0 2 1 2 1 2 0 2 = = = = = = K Q J Q K Q J K Q J n n n n 0 Q n 1 Q n ( 4 ) 检查自启动。 该计数器的无效状态为 000 和 111 ,将 000 状态代入状态方程中进行核算后得 111 ,为无效状态;将 111 状态代入状态方程中计算得 000 ,也为无效状态。可见,该计数器一旦进入无效状态后,电路只能在无效状态中循环,而不能自启动。 为了使计数器能自启动,需要对原方案进行如下修改。 10 Q 2 n Q 1 n Q 0 n 0 1 00 01 11 1 × 1 0 0 × 1 Q 2 n +1 卡 诺 图 0 10 Q 2 n Q 1 n Q 0 n 0 1 00 01 11 1 × 1 0 0 × 1 Q 2 n +1 卡 诺 图 0 修改后的状态方程 修改后的驱动方程 方案修改后,再次将无效状态 000 和 111 代入状态方程,可得相应次态为 011 和 000 ,可见电路能自启动。 ( 5 ) 根据驱动方程和输出方程画逻辑图。 FF 0 1J 1K C1 FF 1 1J C1 FF 2 1J C1 CP 1K Q 1 & & 1K 1 Y Q 0 Q 0 Q 1 Q 2 Q 2 n n n Q Q Y 0 2 1 = + , , , 0 1 0 2 1 2 1 2 1 2 = = = = = = K Q J Q K Q J K Q J n n n n 0 Q n 1 Q n n Q 0 例:设计一个串行数据检测器,要求在连续输入三个或三个以上“ 1” 时输出为 1 ,其余情况下输出为 0 。 一、抽象、画出状态转换图 二、状态化简 用 X ( 1 位)表示输入数据 用 Y ( 1 位)表示输出(检测结果) 三、状态分配 取 n=2 ,令 的 00 、 01 、 10 为 则, 四、选用 JK 触发器,求方程组 五、画逻辑图 六、检查电路能否自启动 将状态“ 11” 代入状态方程和输出方程,分别求 X=0/1 下的次态和现态下的输出,得到: 能自启动 6.6 用 multisim 分析时序逻辑电路 例 : 分析下图的计数器电路。求电路的时序图 . 说明这是几进制的计数器。查看更多