【物理】2019届一轮复习人教版机械振动学案

【物理】2019届一轮复习人教版机械振动学案

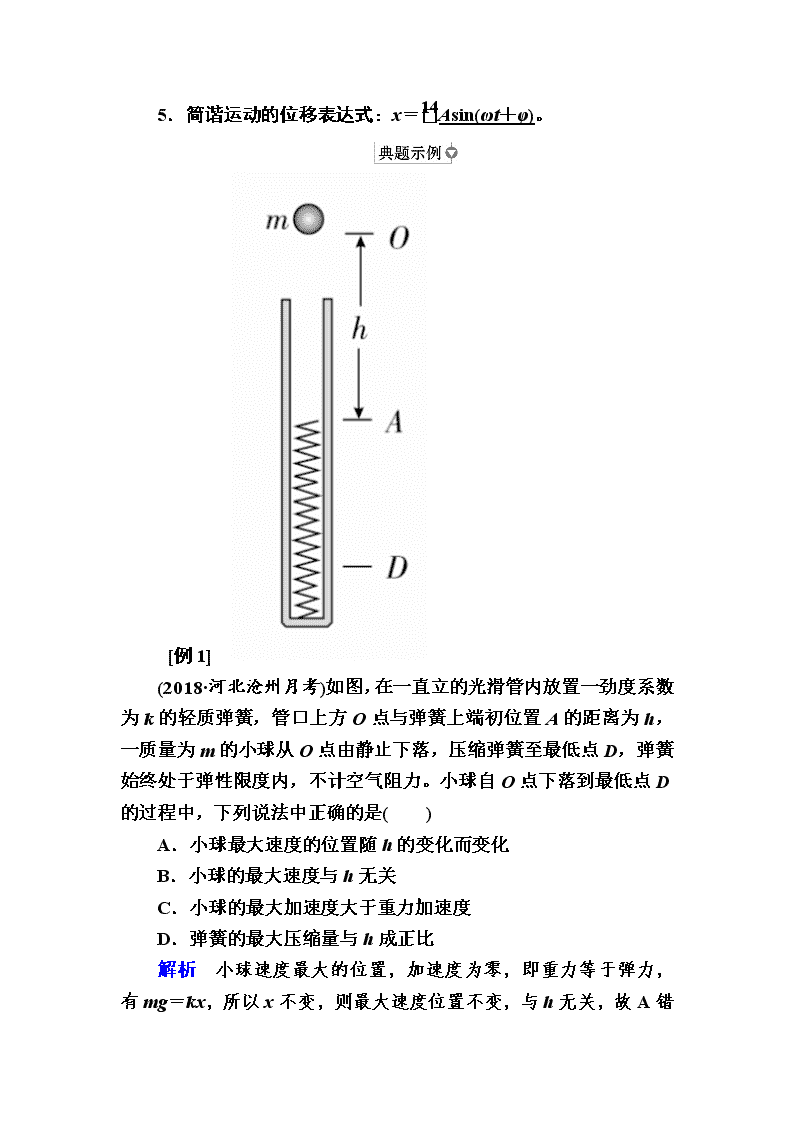
选修 3－4 考纲要求 复习指南 内容 要求 简谐运动 Ⅰ 简谐运动的公式和图象 Ⅱ 单摆、单摆的周期公式 Ⅰ 受迫振动和共振 Ⅰ 机械波、横波和纵波 Ⅰ 横波的图象 Ⅱ 波速、波长和频率(周期)的关系 Ⅰ 波的干涉和衍射现象 Ⅰ 多普勒效应 Ⅰ 实验一：探究单摆的运动、用单摆 测定重力加速度 电磁波的产生 Ⅰ 电磁波的发射、传播和接收 Ⅰ 电磁波谱 Ⅰ 光的折射定律 Ⅱ 折射率 Ⅰ 全反射、光导纤维 Ⅰ 光的干涉、衍射和偏振现象 Ⅰ 狭义相对论的基本假设 Ⅰ 质能关系 Ⅰ 实验二：测定玻璃的折射率 实验三：用双缝干涉测光的波长 考情分析： 1．机械振动和机械波的 考查以图象为主，通过简 谐运动的图象研究振动 的特点和规律，通过机械 波的图象研究波的形成 与传播规律。 2．机械振动和机械波部 分常以弹簧振子或单摆 为载体，考查简谐运动规 律。结合波动问题，考查 简谐运动。 3．光学部分主要考查光 的折射、全反射等光的传 播规律，要重视折射率公 式和临界角公式，重视数 理相结合的方法。 命题趋势： 　基本概念、机械波多以 选择题的形式出现。 机械波的部分内容及光 的折射、全反射多以计算 题的形式来考查。 说明： 1．简谐运动只限于单摆 和弹簧振子 2．简谐运动的公式只限 于回复力公式；图象只限 于位移—时间图象 3．光的干涉限于双缝干 涉、薄膜干涉 第 53 课时　机械振动 考点 1　简谐运动的特征 1．定义：物体在跟位移大小成正比并且总是指向平衡位置的 回复力作用下的振动。 2．平衡位置：物体在振动过程中回复力为零的位置。 3．回复力 (1)定义：使物体返回到平衡位置的力。 (2)方向：总是指向平衡位置。 (3)来源：属于效果力，可以是某一个力，也可以是几个力的 合力或某个力的分力。 4．描述简谐运动的物理量 (1)位移 x：由平衡位置指向质点所在位置的有向线段，是矢 量。 (2)振幅 A：振动物体离开平衡位置的最大距离，是□10 标量，表 示振动的强弱。 (3)周期 T：物体完成一次□11 全振动所需的时间。 频率 f：单位时间内完成全振动的□12 次数。 它们是表示振动快慢的物理量，二者的关系为 T＝□13 1 f 。 5．简谐运动的位移表达式：x＝□14 Asin(ωt＋φ)。 [例 1]　 (2018·河北沧州月考)如图，在一直立的光滑管内放置一劲度系数 为 k 的轻质弹簧，管口上方 O 点与弹簧上端初位置 A 的距离为 h， 一质量为 m 的小球从 O 点由静止下落，压缩弹簧至最低点 D，弹簧 始终处于弹性限度内，不计空气阻力。小球自 O 点下落到最低点 D 的过程中，下列说法中正确的是(　　) A．小球最大速度的位置随 h 的变化而变化 B．小球的最大速度与 h 无关 C．小球的最大加速度大于重力加速度 D．弹簧的最大压缩量与 h 成正比 解析　小球速度最大的位置，加速度为零，即重力等于弹力， 有 mg＝kx，所以 x 不变，则最大速度位置不变，与 h 无关，故 A 错 误；小球从下落点到平衡位置，重力和弹力做功，下落的高度不同， 小球的最大速度不同，故 B 错误；若小球在 A 点释放，根据简谐运 动的对称性，在最低点加速度为 g，方向向上，若小球在 O 点释放， 最低点位置会下降，则最大加速度大于 g，故 C 正确；在最低点弹簧 的压缩量最大，根据能量守恒定律可得 mg(h＋x)＝1 2 kx2，故弹簧的最 大压缩量与 h 有关，但不是成正比关系，故 D 错误。 答案　C 质点做简谐运动时，其位移(相对平衡位置的位移)、回复力、加 速度、速度、动量等矢量都随时间做周期性的变化，它们的周期就是 简谐运动的周期 T。物体的动能和势能也随时间做周期性的变化，其 周期为T 2 ，常见的简谐运动模型有弹簧振子和单摆。 1．(多选)下列关于振动的回复力的说法正确的是(　　) A．回复力方向总是指向平衡位置 B．回复力是按效果命名的 C．回复力一定是物体受到的合力 D．回复力由弹簧的弹力提供 E．振动物体在平衡位置所受的回复力是零 答案　ABE 解析　回复力是按效果命名的，是指向平衡位置使振动物体回到 平衡位置的力，可以由某个力或某几个力的合力提供，也可以由某个 力的分力提供，故 A、B 正确，C 错误；在水平弹簧振子中弹簧的弹 力提供回复力，但在其他振动中，不一定由弹簧弹力提供，D 错误； 振动物体在平衡位置受到的回复力是零，E 正确。 2．(多选)关于简谐运动的周期，以下说法正确的是(　　) A．间隔一个周期的整数倍的两个时刻，物体的振动情况相同 B．间隔半个周期的奇数倍的两个时刻，物体的速度和加速度可 能同时相同 C．半个周期内物体的动能变化一定为零 D．一个周期内物体的势能变化一定为零 E．经过一个周期质点通过的路程变为零 答案　ACD 解析　根据周期 T 的定义可知，物体完成一次全振动，所有的物 理量都恢复到初始状态，故 A 正确；当间隔半周期的奇数倍时，所 有的矢量都变得大小相等，方向相反，且物体的速度和加速度不同时 为零，故 B 错误；物体的动能和势能变化的周期为T 2 ，所以 C、D 正 确；经过一个周期，质点通过的路程为 4A，E 错误。 3. (多选)如图，轻弹簧上端固定，下端连接一小物块，物块沿竖直 方向做简谐运动。以竖直向上为正方向，物块简谐运动的表达式为 y ＝0.1 sin(2.5πt) m。t＝0 时刻，一小球从距物块 h 高处自由落下；t＝ 0.6 s 时，小球恰好与物块处于同一高度。取重力加速度的大小 g＝10 m/s2。以下判断正确的是(　　) A．h＝1.7 m B．简谐运动的周期是 0.8 s C．0.6 s 内物块运动的路程是 0.2 m D．t＝0.4 s 时，物块与小球运动方向相反 E．t＝0.6 s 时，物块的位移是－0.1 m 答案　ABE 解析　t＝0.6 s 时，物块的位移为 y＝0.1sin(2.5π×0.6) m＝－0.1 m；则对小球 h＋|y|＝1 2 gt2，解得 h＝1.7 m，A、E 正确；简谐运动的 周期是 T＝2π ω ＝ 2π 2.5π s＝0.8 s，B 正确；0.6 s 内物块运动的路程是 3A ＝0.3 m，C 错误；t＝0.4 s＝T 2 ，此时物块在平衡位置向下振动，则此 时物块与小球运动方向相同，D 错误。 考点 2　　简谐运动图象的应用 1．物理意义：表示振动质点的位移随时间变化的规律。 2．图象特征 (1)正弦(或余弦)曲线。 (2)从质点位于平衡位置处开始计时，函数表达式为 x＝Asinωt， 图象如图甲所示；从质点位于最大位移处开始计时，函数表达式为 x＝Acosωt，图象如图乙所示。 (3)图象斜率表示速度大小和方向，平衡位置速度最大，偏离平 衡位置位移最大时速度最小等于 0，质点的运动方向根据图象斜率判 断，斜率为正表示运动方向为正方向，斜率为负表示运动方向为负方 向。 [例 2]　(2017·浙江舟山模拟)(多选)甲、乙两弹簧振子，振动图象 如图所示，则可知(　　) A．两弹簧振子完全相同 B．两弹簧振子所受回复力最大值之比 F 甲∶F 乙＝2∶1 C．振子甲速度为零时，振子乙速度最大 D．两振子的振动频率之比 f 甲∶f 乙＝1∶2 解析　从图象中可以看出，两弹簧振子周期之比 T 甲∶T 乙＝2∶ 1，得频率之比 f 甲∶f 乙＝1∶2，D 正确；弹簧振子周期与振子质量、 弹簧劲度系数 k 有关，周期不同，说明两弹簧振子不同，A 错误；由 于弹簧的劲度系数 k 不一定相同，所以两振子所受回复力(F＝－kx) 的最大值之比 F 甲∶F 乙不一定为 2∶1，所以 B 错误；由简谐运动的 特点可知，在振子到达平衡位置时位移为零，速度最大；在振子到达 最大位移处时，速度为零，从图象中可以看出，在振子甲到达最大位 移处时，振子乙恰好到达平衡位置，所以 C 正确。 答案　CD (1)分析简谐运动过程中要特别注意简谐运动的周期性和对称性。 (2)分析简谐运动过程中要简谐运动场景和运动图象(x­t)相结合 对应分析。 (3)分析简谐运动中各物理量的变化情况时，一定要以位移为桥 梁，位移增大时，振动质点的回复力、加速度、势能均增大，速度、 动能均减小，反之，则产生相反的变化。另外，各矢量均在其值为零 时改变方向。 (人教版选修 3－4 P5·T3 改编)一质点做简谐运动的图象如图所 示，下列说法正确的是(　　) A．质点振动频率是 4 Hz B．在 10 s 内质点经过的路程是 20 cm C．第 4 s 末质点的速度是零 D．在 t＝1 s 和 t＝3 s 两时刻，质点位移大小相等、方向相同 答案　B 解析　由题图可知，该简谐运动的周期为 4 s，频率为 0.25 Hz，A 错误；在 10 s 内质点经过的路程是 2.5×4A＝20 cm，B 正确；第 4 s 末质点的速度最大，C 错误；在 t＝1 s 和 t＝3 s 两时刻，质点位移大 小相等、方向相反，故 D 错误。 考点 3　　受迫振动　共振 1．受迫振动 系统在驱动力作用下的振动。做受迫振动的物体，它做受迫振 动的周期(或频率)等于驱动力的周期(或频率)，而与物体的固有周 期(或频率)无关。 2．受迫振动中系统能量的转化：受迫振动系统机械能不守恒， 系统与外界时刻进行能量交换。 3．共振 做受迫振动的物体，它的驱动力的频率与固有频率越接近，其振 幅就越大，当二者相等时，振幅达到最大，这就是共振现象。共 振曲线如图所示。 1. (多选)如图所示，曲轴上挂一个弹簧振子，转动摇把，曲轴可带 动弹簧振子上下振动。开始时不转动摇把，让振子自由振动，测得其 频率为 2 Hz。现匀速转动摇把，转速为 240 r/min。则(　　) A．当振子稳定振动时，它的振动周期是 0.5 s B．当振子稳定振动时，它的振动频率是 4 Hz C．当转速增大时，弹簧振子的振幅增大 D．当摇把转动的频率减小到接近弹簧振子的频率时，弹簧振子 的振幅增大 E．弹簧振子的振幅与转速有关 答案　BDE 解析　摇把匀速转动的频率f＝240 60 Hz＝4 Hz，周期T＝1 f ＝0.25 s， 当振子稳定振动时，它的振动周期及频率均与驱动力的周期及频率相 等，A 错误、B 正确；当摇把的频率接近振子的固有频率时，弹簧振 子的振幅将增大，C 错误，D、E 正确。 2．(人教版选修 3－4 P19 演示实验改编)(多选)如图所示，A、B、 C、D 四个单摆的摆长分别为 l、2l、l、l 2 ，摆球的质量分别为 2m、 2m、m、m 2 ，四个单摆静止地悬挂在一根水平细线上。现让 A 球振动 起来，通过水平细线迫使 B、C、D 也振动起来，则下列说法错误的 是(　　) A．A、B、C、D 四个单摆的周期均相同 B．只有 A、C 两个单摆的周期相同 C．B、C、D 中因 D 的质量最小，故其振幅是最大的 D．B、C、D 中 C 的振幅最大 E．B、C、D 中 C 的振幅最小 答案　BCE 解析　在 A 的驱动下，B、C、D 均做受迫振动，受迫振动的频 率均与驱动力的频率(A 的固有频率)相等，与各自的固有频率无关，A 正确、B 错误；判断能否达到最大振幅，即实现共振，取决于 f 固是 否与 f 驱相等。对于单摆而言，固有频率与摆球质量无关，所以不必 考虑摆球的质量。B、C、D 中，只有 C 的固有频率等于驱动力的频 率，所以 B、C、D 中 C 的振幅最大，C、E 错误，D 正确。 3．(人教版选修 3－4 P21·T4 改编)(多选)一个单摆在地面上做受 迫振动，其共振曲线(振幅 A 与驱动力频率 f 的关系)如图所示，则下 列说法正确的是(g 取 10 m/s2)(　　) A．此单摆的固有周期约为 2 s B．此单摆的摆长约为 1 m C．若摆长增大，单摆的固有频率增大 D．若摆长增大，共振曲线的峰将向左移动 E．此单摆的振幅是 8 cm 答案　ABD 解析　由共振曲线知此单摆的固有频率为 0.5 Hz，固有周期为 2 s；再由 T＝2π l g 得此单摆的摆长约为 1 m；若摆长增大，则单摆的 固有周期增大，固有频率减小，共振曲线的峰将向左移动，A、B、D 正确，C 错误；此单摆做受迫振动，只有共振时的振幅最大，为 8 cm，E 错误。 考点 4　　用单摆测重力加速度 1．实验原理：由单摆的周期公式 T＝2π l g ，可得出 g＝4π2 T2 l，测出单摆的摆长 l 和振动周期 T，就可求出当地的重力加速度 g。 2．实验步骤 (1)做单摆：取约 1 m 长的细丝线穿过带中心孔的小钢球，并打 一个比小孔大一些的结，然后把线的另一端用铁夹固定在铁架台上， 让摆球自然下垂，如图所示。 (2)测摆长：用毫米刻度尺量出摆线长 L(精确到毫米)，用游 标卡尺测出小球直径 D，则单摆的摆长 l＝L＋D 2 。 (3)测周期：将单摆从平衡位置拉开一个角度(小于5°)，然后释 放小球，记下单摆摆动30～50 次的总时间，算出平均每摆动一次的 时间，即为单摆的振动周期。 (4)改变摆长，重做几次实验。 3．数据处理 (1)公式法：g＝4π2 T2 l。 (2)图象法：画 l­T2 图象。则斜率 k＝ g 4π2 ，那么 g＝□10 4π2k。 4．注意事项 (1)选用 1 m 左右的细线。 (2)悬线顶端不能晃动，需用夹子夹住，保证顶点固定。 (3)小球在同一竖直面内摆动，且摆角小于 5°。 (4)选择在摆球摆到平衡位置处开始计时，并数准全振动的次数。 (5)小球自然下垂时，用毫米刻度尺量出悬线长 l′，用游标卡尺 测量小球的直径，然后算出摆球的半径 r，则摆长 l＝l′＋r。 [例 3]　(1)在利用单摆测定重力加速度的实验中，若测得的 g 值 偏大，可能的原因是(　　) A．摆球质量过大 B．单摆振动时振幅较小 C．测量摆长时，只考虑了线长，忽略了小球的半径 D．测量周期时，把 n 个全振动误认为(n＋1)个全振动，使周期 偏小 E．测量周期时，把 n 个全振动误认为(n－1)个全振动，使周期 偏大 (2)若单摆是一个秒摆，将此摆移到月球上 (g 月＝1 6g 地 )，其周期 是________。 (3)实验中停表的读数如图，为________s。 解析　(1)由单摆周期公式 T＝2π l g 可知，重力加速度 g＝4π2l T2 ， 进而知重力加速度与摆球质量无关，故 A 错误；重力加速度与单摆 振动的振幅无关，故 B 错误；测量摆长时，只考虑了线长，忽略了 小球的半径，摆长 l 偏小，由 g＝4π2l T2 可知，所测重力加速度偏小， 故 C 错误；测量周期时，把 n 个全振动误认为(n＋1)个全振动，使周 期偏小，由 g＝4π2l T2 可知，所测重力加速度偏大，故 D 正确；测量周 期时，把 n 个全振动误认为(n－1)个全振动，使周期偏大，由 g＝4π2l T2 可知，所测重力加速度偏小，故 E 错误。 (2)在地球上秒摆的周期 T＝2 s，将秒摆移到月球上，其周期 T＝ 2π L g 月＝ 6T＝2 6 s。 (3)由图示停表可知，分针示数为 1 min＝60 s，秒针示数为 10.8 s，则停表示数为 60 s＋10.8 s＝70.8 s。 答案　(1)D　(2)2 6 s　(3)70.8 (1)器材选择：选用体积小、密度大的球；选用质量小、弹性小 的细线。 (2)实验操作：摆动过程中摆长保持不变；摆角不超过 5°；摆球 拉到一定位置由静止释放，防止形成圆锥摆；摆球通过平衡位置时开 始计时。 (3)数据处理：多次测量取平均值计算周期。 某同学在“用单摆测定重力加速度”的实验中进行了如下的操作： (1)用游标尺上有 10 个小格的游标卡尺测量摆球的直径如下图甲 所示，可读出摆球的直径为________cm。把摆球用细线悬挂在铁架 台上，测量摆线长，通过计算得到摆长 L。 (2)用秒表测量单摆的周期，当单摆摆动稳定且到达最低点时开 始计时并记为 n＝1，单摆每经过最低点记一次数，当数到 n＝60 时 秒表的示数如图乙所示，该单摆的周期是 T＝________s(结果保留三 位有效数字)。 (3)测量出多组周期 T、摆长 L 的数值后，画出 T2­L 图线如图丙， 此图线斜率的物理意义是 (　　) A．g B.1 g C.4π2 g D. g 4π2 (4)在(3)中，描点时若误将摆线长当作摆长，那么画出的直线将 不通过原点，由图线斜率得到的重力加速度与原来相比，其大小 (　　) A．偏大 B．偏小 C．不变 D．都有可能 答案　(1)2.06　(2)2.28　(3)C　(4)C 解析　(1)摆球的直径为 d＝20 mm＋6× 1 10 mm＝20.6 mm＝ 2.06 cm。 (2)秒表的读数为 t＝60 s＋7.4 s＝67.4 s，根据题意 t＝60－1 2 T＝59 2 T，所以周期 T＝2t 59 ≈2.28 s。 (3)根据单摆周期公式 T＝2π L g ，可得T2 L ＝4π2 g ＝k(常数)，所以 C 正确。 (4)因为T2 L ＝4π2 g ＝k(常数)，所以ΔT2 ΔL ＝4π2 g ＝k，若误将摆线长当作 摆长，画出的直线将不通过原点，但图线的斜率仍然满足T21－T22 L1－L2 ＝4π2 g ＝k，所以由图线的斜率得到的重力加速度不变。 1．摆长为 L 的单摆做简谐运动，若从某时刻开始计时(取 t＝0)， 当振动至 t＝3π 2 L g 时，摆球具有负向最大速度，则单摆的振动图象 是图中的(　　) 答案　C 解析　单摆周期为 T＝2π L g ，当 t＝3π 2 L g ＝3T 4 时摆球具有负向 最大速度，知摆球经过平衡位置向负方向振动，C 正确，A、B、D 错误。 2．(2016·温州质检)在飞机的发展史中有一个阶段，飞机上天后 不久，机翼很快就抖动起来，而且越抖越厉害，后来人们经过了艰苦 的探索，利用在飞机机翼前缘处装置一个配重杆的方法，解决了这一 问题，装置配重杆的主要目的是(　　) A．加大飞机的惯性 B．使机体更加平衡 C．使机翼更加牢固 D．改变机翼的固有频率 答案　D 解析　飞机飞上天后，在气流周期性驱动力作用下做受迫振动， 机翼越抖越厉害说明气流驱动力周期与机翼的固有周期非常接近或 相等。在机翼前缘处装置配重杆，目的是通过改变机翼的质量来改变 其固有频率，使驱动力频率与固有频率相差较大，从而实现减振的目 的，故 D 正确。 3．做简谐运动的单摆摆长不变，若摆球质量增加为原来的 4 倍， 摆球经过平衡位置时速度减小为原来的1 2 ，则单摆振动的(　　) A．频率、振幅都不变 B．频率、振幅都改变 C．频率不变、振幅改变 D．频率改变、振幅不变 答案　C 解析　由单摆周期公式 T＝2π l g 知周期只与 l、g 有关，与 m 和 v 无关，周期不变，其频率不变；在没改变质量前，设单摆最低点与 最高点高度差为 h，最低点速度为 v，则 mgh＝1 2 mv2，质量改变后有 4mgh′＝1 2 ×4m·( v 2 )2，可知 h′≠h，振幅改变，C 正确。 4．(2016·河南郑州一中调研)有一个在 y 方向上做简谐运动的物 体，其振动图象如图所示，下列关于下图中①～④的判断正确的是 (　　) A．图③可作为该物体的回复力—时间图象 B．图②可作为该物体的回复力—时间图象 C．图①可作为该物体的速度—时间图象 D．图④可作为该物体的加速度—时间图象 答案　A 解析　根据简谐振动回复力 F＝－kx 知，回复力或加速度与位 移大小成正比，方向相反，可得 A 正确，B、D 错误；速度在平衡位 置最大，在最大位移处为零，图②应该为速度—时间图象，C 错误。 5．(2018·山东潍坊月考)(多选)把一个筛子用四根弹簧支撑起来， 筛子上装一个电动偏心轮，它每转一周，给筛子一个驱动力，这就做 成了一个共振筛，如图甲所示。该共振筛的共振曲线如图乙所示。已 知增大电压，可使偏心轮转速提高，增加筛子质量，可增大筛子的固 有周期。现在，在某电压下电动偏心轮转速是 54 r/min。为了使筛子 的振幅增大，下列做法正确的是(　　) A．提高输入电压 B．降低输入电压 C．增加筛子质量 D．减小筛子质量 答案　BD 解析　由题图乙可知筛子的固有频率为 0.8 Hz，那么固有周期为 1.25 s，而现在偏心轮转速为 54 r/min，即周期为10 9 s<1.25 s，为了使 振幅增大，应该使偏心轮的周期更接近筛子的固有周期，所以要增大 偏心轮的转动周期，或减小筛子的固有周期，结合题意可知应该降低 输入电压，或减小筛子质量，故 B、D 正确。 6．(多选)如图甲所示为以 O 点为平衡位置，在 A、B 两点间做 简谐运动的弹簧振子，图乙为这个弹簧振子的振动图象，由图可知下 列说法中正确的是(　　) A．在 t＝0.2 s 时，弹簧振子的加速度为正向最大 B．在 t＝0.1 s 与 t＝0.3 s 两个时刻，弹簧振子在同一位置 C．在 t＝0 到 t＝0.2 s 时间内，弹簧振子做加速度增大的减速运 动 D．在 t＝0.6 s 时，弹簧振子有最小的弹性势能 答案　BC 解析　t＝0.2 s 时，弹簧振子的位移为正向最大值，而弹簧振子 的加速度与位移大小成正比，方向与位移方向相反，A 错误；在 t＝ 0.1 s 与 t＝0.3 s 两个时刻，弹簧振子的位移相同，B 正确；从 t＝0 到 t＝0.2 s 时间内，弹簧振子从平衡位置向正的最大位移处运动，位 移逐渐增大，加速度逐渐增大，加速度方向与速度方向相反，弹簧振 子做加速度增大的减速运动，C 正确；在 t＝0.6 s 时，弹簧振子的位 移为负向最大值，即弹簧的形变最大，弹簧振子的弹性势能最大，D 错误。 7．(多选)弹簧振子做简谐运动，O 为平衡位置，当它经过点 O 时开始计时，经过 0.3 s 第一次到达点 M，再经过 0.2 s 第二次到达点 M，则弹簧振子的周期为(　　) A．0.53 s B．1.4 s C．1.6 s D．3 s 答案　AC 解析　如图甲所示，设 O 为平衡位置，OB(OC)代表振幅，振子 从 O→C 所需时间为T 4 。因为简谐运动具有对称性，所以振子从 M→C 所用时间和从 C→M 所用时间相等，故T 4 ＝0.3 s＋0.2 s 2 ＝0.4 s，解得 T ＝1.6 s，C 正确。 如图乙所示，若振子一开始从平衡位置向点 B 运动，设点 M′ 与点 M 关于点 O 对称，则振子从点 M′经过点 B 回到点 M′所用的 时间与振子从点 M 经过点 C 回到点 M 所需时间相等，即 0.2 s。振子 从点 O 到点 M′和从点 M′到点 O 以及从点 O 到点 M 所需时间相 等，为0.3 s－0.2 s 3 ＝ 1 30 s，故周期为 T＝ (0.5＋ 1 30) s＝16 30 s≈0.53 s，A 正确。 8．如图甲所示是一个摆线长度可调的单摆振动的情景图，O 是 它的平衡位置，P、Q 是小球所能到达的最高位置。小球的质量 m＝ 0.4 kg，图乙是摆线长为 l 时小球的振动图象，g 取 10 m/s2。 (1)为测量单摆的摆动周期，测量时间应从摆球经过____(填“O”“P” 或“Q”)时开始计时；测出悬点到小球球心的距离(摆长)L 及单摆完成 n 次全振动所用的时间 t，则重力加速度 g＝________(用 L、n、t 表 示)。 (2)由图乙写出单摆做简谐运动的表达式，并判断小球在什么位 置时加速度最大？最大加速度为多少？ 答案　(1)O　4π2n2L t2 　(2)x＝5sinπt(cm)　小球在最大位移处的 加速度最大' 0.5 m/s2 解析　(1)因摆球经过最低点的速度大，容易观察和计时，所以 测量时间应从摆球经过最低点 O 开始计时，单摆周期 T＝t n ，再根据 单摆周期公式 T＝2π L g ，可解得 g＝4π2n2L t2 。 (2)由图乙可知单摆的振幅 A＝5 cm，ω＝2π T ＝2π 2 rad/s＝π rad/s， 所以单摆做简谐运动的表达式为 x＝5sinπt(cm)。小球在最大位移处 的加速度最大，由图乙可看出此摆的周期是 2 s，根据 T＝2π L g ，可 求 得 摆 长 为 L ＝ 1 m ， 加 速 度 最 大 值 am ＝ Fm m ＝ mgsinθ m ＝ gA L ＝ 10 × 5 × 10－2 1 m/s2＝0.5 m/s2。 9．(2016·北京高考)如图所示，弹簧振子在 M、N 之间做简谐运 动。以平衡位置 O 为原点，建立 Ox 轴，向右为 x 轴正方向。若振子 位于 N 点时开始计时，则其振动图象为(　　) 答案　A 解析　振子在 N 点时开始计时，其位移为正向最大，并按余弦 规律变化，A 正确。 10. (2017·北京高考)某弹簧振子沿 x 轴的简谐运动图象如图所示，下 列描述正确的是(　　) A．t＝1 s 时，振子的速度为零，加速度为负的最大值 B．t＝2 s 时，振子的速度为负，加速度为正的最大值 C．t＝3 s 时，振子的速度为负的最大值，加速度为零 D．t＝4 s 时，振子的速度为正，加速度为负的最大值 答案　A 解析　t＝1 s 时，振子处于正的最大位移处，振子的速度为零， 加速度为负的最大值，A 正确；t＝2 s 时，振子在平衡位置且向 x 轴 负方向运动，则振子的速度为负，加速度为零，B 错误；t＝3 s 时， 振子处于负的最大位移处，振子的速度为零，加速度为正的最大值，C 错误；t＝4 s 时，振子在平衡位置且向 x 轴正方向运动，则振子的速 度为正，加速度为零，D 错误。 11．(2017·安徽皖南八校联考)如图甲所示在一条张紧的绳子上挂 几个摆，当 a 摆振动的时候，通过张紧的绳子给其他各摆施加驱动力， 使其余各摆也振动起来，达到稳定时________摆的振幅最大，图乙是 c 摆稳定以后的振动图象，重力加速度为 g，不计空气阻力，则 a 摆 的摆长为________。 答案　c　gt20 4π2 解析　根据单摆周期公式 T＝2π L g 可知，图甲所示中，单摆的 固有周期关系为 Ta＝Tc

查看更多