【物理】2019届二轮复习小船渡河模型学案(全国通用)
模型界定
本模型是解决以小船渡河为载体的不同参考系中运动转换的问题,具体包括小船渡河、骑马射箭等。
模型破解
1.合运动与分运动的关键特征| |k ]
(i)等时性
合运动与分运动是同时发生的,所用时间相等,可由任一分运动或合运动求解小船运动的时间。
(ii)等效性
合运动的效果与几个分运动叠加后后的共同效果完全相同。
(iii)独立性
一个物体同时参与几个分运动,各个分运动相互独立,任一分运动不受其它分运动的影响。
2. 小船渡河问题的处理方法
设小船在静止水中的匀速运动的速度是 v 1 ,均匀流动的河水的速度是 v 2 , 河宽为 d 。 又设 v1 与河岸的夹角为θ( 0≤θ≤1800 ),合速度v与河岸夹角为 。
(i)分解法
图1
如图 1 ,沿平行于河岸与垂直于河岸的方向上建立直角坐标系,将 v1分解为v1x=v1cosθ和 v1y =v1sinθ ,则vx= v1x +v2 =v1cosθ+ v2、vy=v1y = v1sinθ。
①合速度
②合位移
③渡河时间
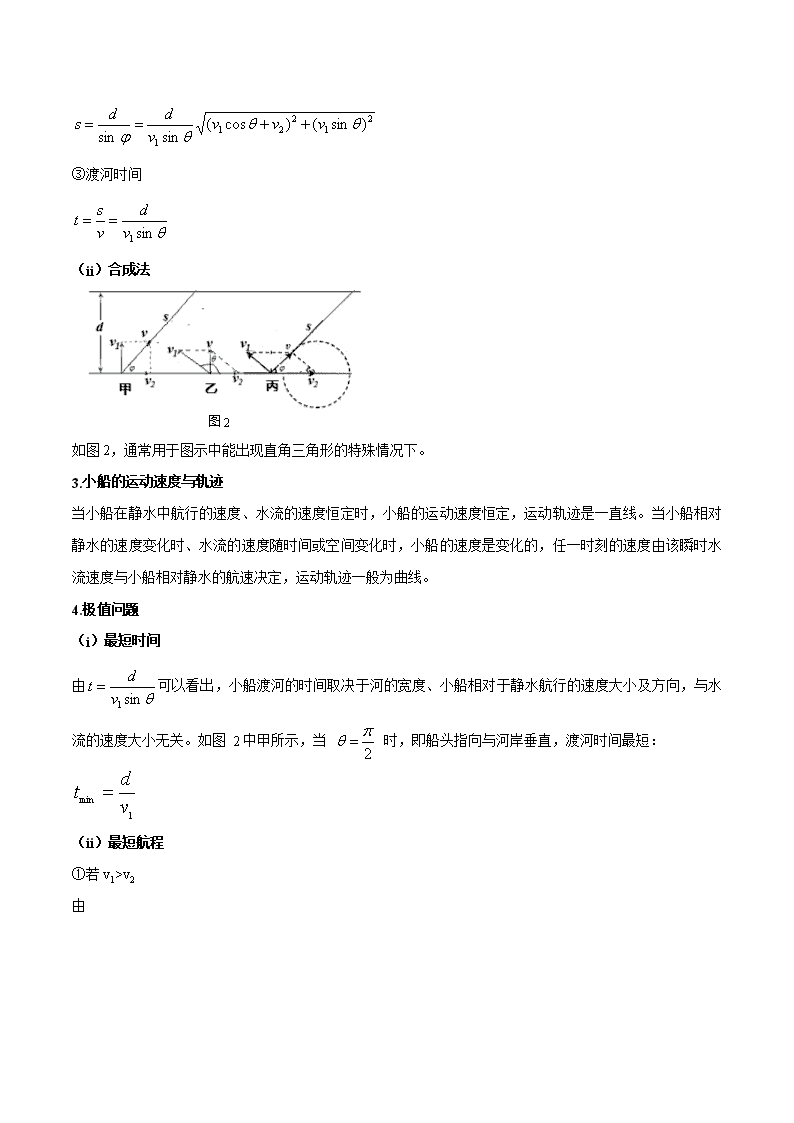
(ii)合成法
图2
如图2,通常用于图示中能出现直角三角形的特殊情况下。
3.小船的运动速度与轨迹
当小船在静水中航行的速度、水流的速度恒定时,小船的运动速度恒定,运动轨迹是一直线。当小船相对静水的速度变化时、水流的速度随时间或空间变化时,小船的速度是变化的,任一时刻的速度由该瞬时水流速度与小船相对静水的航速决定,运动轨迹一般为曲线。
4.极值问题
(i)最短时间
由可以看出,小船渡河的时间取决于河的宽度、小船相对于静水航行的速度大小及方向,与水流的速度大小无关。如图 2中甲所示,当 时,即船头指向与河岸垂直,渡河时间最短:
(ii)最短航程
①若v1>v2
由
可知当 v1cosθ+v2=0 时s min =d,此时,船头指向上游,如图2中乙所示。这时由v1cosθ+v2=0可知船相对于静水的速度v1 沿河岸向上分量与水流速相等,此时合速度方向垂直于河岸即,渡河的位移最小。
②若v1
v1,下面用小箭头表示小船及船头的指向,则能正确反映小船在最短时间内渡河、最短位移渡河的情景图示依次是
学+ + ]
A. ①② B.①⑤ C.④⑤ D.②③
【答案】C
【解析】小船以最短时间渡河时,因河流宽度一定,就要求小船在垂直于河岸方向上的分速度最大,即小船相对于静水的航行方向也即船头的指向须始终垂直于河岸,则此时小船的实际运动方向必偏向于下游,应选④。当小船以最短的路程渡河时,由于v2>v1,小船可垂直到达河对岸,此时船头的指向应偏向于河上游,对应于图⑤,故C正确。
(iii)最小速度
在小船渡河时,若对小船被水流沿河冲下的距离加以限制时,或者对小船实际运动的方向加以限制时,则小船相对于静水航行的速度存在一个最小值。
图3
如图3,河宽为d,小船渡河时允许被水流冲下的距离不超过s,水流速度为v2。设小船的最小速度为v1,船头指向与河岸上游间的夹角为θ时小船恰好在到达对岸时被冲下的距离为s。由、有
其中。
可见当时
由图中可以看到,此时,即此时船头的指向与小船的合速度垂直,故也可通过作图法确定小船的最小速度:
以v2的顶点为圆心,以v1的大小为半径作圆,小船以最小速度恰好能按要求到达对岸时,小船航线恰在出发点与对岸临界点的连线上,且船的最小速度v1与该连线垂直,由几何关系可得,即。
例2.如图所示,河水的流速为4m/s,一条船要从河的南岸A点沿与河岸成30°角的直线航行到北岸下游某处,则船的开行速度(相对于水的速度)最小为
例2题图
A.2m/s B.3m/s C.4m/s D.5m/s
【答案】A
模型演练
7.如图所示,一条小船位于200 m宽的河正中A点处,从这里向下游100 m处有一危险区,当时水流速度为4 m/s,为了使小船避开危险区沿直线到达对岸,小船在静水中的速度至少是( )
练8图
A. m/s B. m/s
C.2 m/s D.4 m/s
【答案】C
【解析】恰使小船避开危险区,小船应沿直线AB到达对岸,如图所示,
练8答图
则有tanθ===,所以θ=30°.当船头与AB垂直时,小船在静水中的速度最小.最小速度为v1=v2sinθ=4sin30° m/s=2 m/s,故C正确.
5.同一河流中两条船的运动或一条船的两个过程
无论是两条船在同一河流中渡河还是一条船在同一河流中经历两个不同的过程,它们之间的关键联系是水流速度相同,利用合成法解决问题时,将两速度合成的矢量图作在一起,是解决问题的捷径。
例3.甲乙两船在静水中航行的速度分别为v1、v2,两船从同一渡口向河对岸划去,已知甲想以最短的时间过河,乙船想以最短的航程过河,结果两船到达对岸的地点恰好相同,假设河水的流速不变,则甲乙两船的渡河时间之比t1:t2为
A. B. C. D.
【答案】A
例4(11江苏3.)如图所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直,且OA=OB。若水流速度不变,两人在靜水中游速相等,则他们所用时间t甲、t乙的大小关系为
例4图
A.t甲<t乙 B.t甲=t乙
C.t甲>t乙 D.无法确定
【答案】C
模型演练
8.如图所示为一条河流,河水流速为v。一只船从A点先后两次渡河到对岸,船在静水中行驶的速度为u。第一次船头向着AB方向行驶,渡河时间tl,船的位移s1;第二次船头向着AC方向行驶,渡河时间t2,船的位移s2。若AB、AC与河岸的垂线的夹角相等,则有
练8图
A. tl>t2 s1s2
C. t1=t2 s1s2
【答案】D
【解析】设AB、AC与河岸垂线之间的夹角为,则两次航行的时间相等,而沿水流方向上的位移,再由可知,D正确.
9.小船匀速横渡一条宽120m的河流,当船头垂直于河岸方向航行时,30s到达河对岸下游60m处,则船在静水中的速度为 ;若船头保持与河岸上游成α角航行,恰好到达正对岸,则α= 。
【答案】2m/s,60
【解析】当船头垂直于河岸航行时,船在垂直于河岸方向上的速度等于船在静水中的航速:
;船在沿河岸方向上的速度等于水流速度:.实际航向垂直于河岸时,
,有.
10.某人乘船横渡一条小河,船在静水中的速度和水速一定,若渡河最短时间为t1,用最短位移渡河时间为t2,则船速与水速之比为多少? 学 ]
【答案】
11.王聪同学,为了测量某河流的水速,找来一条小船,他首先保持小船对水以恒定的速度行驶.第一次,保持船头始终垂直河岸划行,经10min到达正对岸下游120m处;第二次,船头始终保持指向与上游河岸成θ角划行,经12.5min到达正对岸。由此,你帮王聪同学计算计算,水速u= ,船对水的速度v= ,河宽L= .
【答案】0.2m/s,,200m
【解析】第一次过程中由于船头始终垂直河岸,则船在垂直河岸方向上的分速度为船对水的速度v,沿河岸方向上的分速度为水速u,有
L=vt1、ut1=x
第二次过程中实际航向垂直于河岸,由运动的合成与分解有
L=vsint2、vcos=u
联立以上各式并将t1=10min、t2=12.5min、x=120m代入可得
、u=0.2m/s、L=200m.
12.甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为v0,划船速度均为v,出发时两船相距为H,甲、乙两船船头均与河岸成60°角,如图所示,已知乙船恰好能垂直到达对岸A点,则下列判断正确的是 ( )
练12图
A.甲、乙两船到达对岸的时间不同
B.v=2v0
C.两船可能在未到达对岸前相遇
D.甲船也在A点靠岸
【答案】BD
6."类渡河"问题
小船渡河问题的实质是利用矢量运算进行参考系的转换,由于参考系转换的运算法则与具体物理情景无关,故涉及参考系变换的问题都可归结于此模型中.
例5. 民族运动会上有一个骑射项目,运动员骑在奔驰的马背上,弯弓放箭射击侧向的固定目标.若运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭的速度为v2,直线跑道离固定目标的最近距离为d,要想在最短的时间内射中目标,则运动员放箭处离目标的距离应该为( )
例5题图
A. B. C. D.
【答案】B
【解析】类比于小船渡河,此是中运动员相当于水流,箭相当于小船。如图所示,
v2
v1
d
x
例5答图
例6.如图所示,在一次救灾工作中,一架沿水平直线飞行的直升机A用悬索将伤员B吊起,直升机A和伤员B以相同水平速度匀速运动的同时,悬索将伤员吊起,在某一段时间内,A、B之间的距离l与时间t的关系为l =H -bt2(式中l表示伤员到直升机的距离,H表示开始计时时伤员与直升机的距离,b是一常数,t表示伤员上升的时间),不计伤员和绳索受到的空气阻力,这段时间内从地面上观察,下面判断正确的是( )
A
B
L
v
例6题图
A.悬索始终保持竖直 B.伤员做直线运动
C.伤员做曲线运动 D.伤员的加速度大小、方向匀不变
【答案】ACD
【解析】此题中飞机相当于水流,伤员相当于小船。伤员B参与了两个方向上的运动:在水平方向上,伤员B和飞机A以相同的速度做匀速运动;在竖直方向上,由于A、B之间的距离以l=H-bt2
规律变化,所以伤员与水面之间的竖直距离关系式为h=H-l=bt2=at2,所以伤员在竖直方向上以2 b的加速度做匀加速直线运动,则伤员做加速度大小、方向均不变的曲线运动,且速度一直增加,故B错误CD正确.由于伤员在水平方向上做匀速运动,水平方向上没有加速度,悬索应成竖直状态,故A选项正确。
模型演练
13.如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度
练13图
(A)大小和方向均不变 (B)大小不变,方向改变
(C)大小改变,方向不变 (D)大小和方向均改变
【答案】A
14.如图所示,民族运动会上有一个骑射项目,运动员骑在奔弛的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标。假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d。若不计空气阻力的影响,要想命中目标且射出的箭在空中飞行时间最短,则( )
A
B
O
练14图
A.运动员放箭处离目标的距离为
B.运动员放箭处离目标的距离为
C.箭射到靶的最短时间为
D.箭射到靶的最短时间为
【答案】BC