云南省曲靖市中考数学试卷及答案

云南省曲靖市中考数学试卷及答案

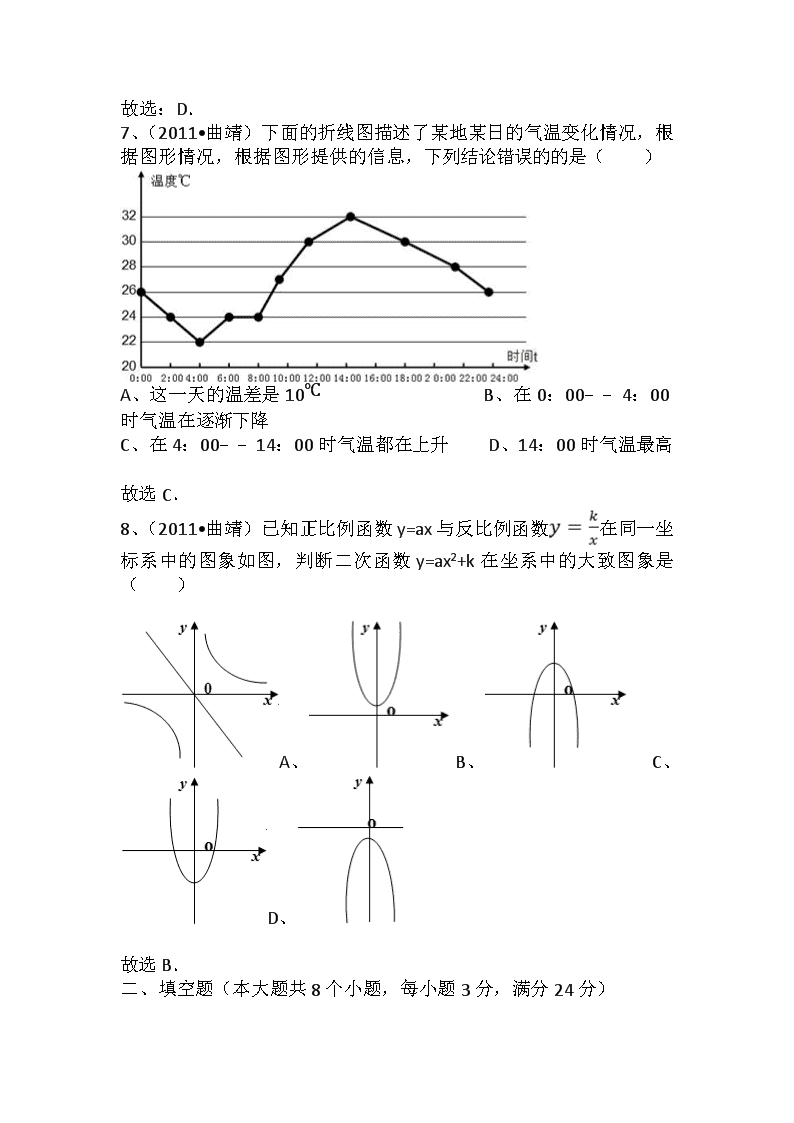
‎2011年云南省曲靖市中考数学试卷 一、选择题（本大题共8个小题，每小题3分，满分24分）‎ ‎1、（2011•曲靖）计算﹣12的结果是（　　）‎ ‎ A、﹣1 B、‎1 ‎C、﹣2 D、2‎ 故选：A．‎ ‎．‎ ‎2、（2011•曲靖）下列计算正确的是（　　）‎ ‎ A、a2+a2=a4 B、a6÷a2=a‎3 ‎C、a•a2=a3 D、（a2）3=a5‎ 故选C．‎ ‎3、（2011•曲靖）用科学记数法表示的如下事实：地球绕太阳公转的速度是1.1×105千米/时；1纳米=1×10﹣‎9米；一天有8.64×104秒；一个氢原子的质量是1.67×10﹣27千克．仅从数的大小来说，其中最大的一个数是（　　）‎ ‎ A、1.1×105 B、1×10﹣9‎ ‎ C、8.64×104 D、1.67×10﹣27 ‎ 故选A ‎4、（2011•曲靖）方程2x﹣y=1和2x+y=7的公共解是（　　）‎ ‎ A、 B、 C、 D、‎ 故选：D．‎ ‎5、（2011•曲靖）点P（m﹣1，‎2m+1）在第二象限，则m的取值范围是（　　）‎ A、 B、 C、m＜1 D、‎ 故选：B．‎ ‎6、（2011•曲靖）将如图所示的两个平面图形绕轴旋转一周，对其所得的立体图形，下列说法正确的是（　　）‎ ‎ A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同 ‎．‎ 故选：D．‎ ‎7、（2011•曲靖）下面的折线图描述了某地某日的气温变化情况，根据图形情况，根据图形提供的信息，下列结论错误的的是（　　）‎ A、这一天的温差是‎10℃‎ B、在0：00﹣﹣4：00时气温在逐渐下降 C、在4：00﹣﹣14：00时气温都在上升 D、14：00时气温最高 故选C．‎ ‎8、（2011•曲靖）已知正比例函数y=ax与反比例函数在同一坐标系中的图象如图，判断二次函数y=ax2+k在坐系中的大致图象是（　　）‎ A、 B、 C、D、‎ 故选B．‎ 二、填空题（本大题共8个小题，每小题3分，满分24分）‎ ‎9、（2010•红河州）﹣的相反数是 解答：解：﹣的相反数是﹣（﹣）=．‎ ‎10、（2011•曲靖）小明、小辉两家所在位置关于学校中心对称．如果小明家距学校2公里，那么他们两家相距　　公里．‎ 故答案为：4．‎ ‎11、（2011•曲靖）某种药品的说明书上标明保存温度是（20±2）℃，请你写出一个适合药品保存的温度　　．‎ 故答案为：18℃～‎‎22℃‎ ‎12、（2011•曲靖）将一列整式按某种规律排成x，﹣2x2，4x3，﹣8x4，16x5…则排在第六个位置的整式为 　．‎ 故答案为：﹣32x6．‎ ‎13、（2011•曲靖）已知△ABC中，DE∥BC，EF∥AB，AB=3，BC=6，AD：DB=2：1，则四边形DBFE的周长为　　．‎ 故答案为：10．‎ ‎．‎ ‎14、（2011•曲靖）一段时间内，鞋店为了解某牌女鞋的销售情况，对各种尺码鞋的销量进行了统计分析，在“平均数”、“中位数”、“众数”、“方差”等统计量中，店主最关注的统计量是　　．‎ 故答案为众数．‎ ‎15、（2011•曲靖）珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，如图，若∠ABC=120°，∠BCD=80°，则∠CDE=　　度．‎ ‎ ‎ 故答案为：20°．‎ ‎16、（2011•曲靖）如图，等边三角形ABC的边长是‎6cm，BD是中线，延长BC至E，使CE=CD，连接DE，则DE的长是　 cm．‎ 故答案为3．‎ 三、解答题（本大题共8个小题，满分72分）‎ ‎17、（2011•曲靖）计算：．‎ 解答：解：原式=2+1﹣2+2‎ ‎=3．‎ ‎18、（2011•曲靖）先化简，再求值：，其中a=．‎ ‎．‎ 解答：解：原式=﹣×‎ ‎=﹣‎ ‎=‎ ‎=，‎ 当a=﹣2时，‎ 原式==．‎ ‎20、（2011•曲靖）甲乙两个工程队合修一条公路，甲工程队比乙工程队每天多修‎50米，甲工程队修‎900米所用时间和乙工程队修‎600米所用时间相等，问甲乙两个工程队每天分别修多少米？‎ 解答：解：设乙工程队每天修x米，则甲工程队每天修（x+50）米．‎ ‎=，‎ 解得x=100，‎ 经检验x=100是原方程的解，‎ ‎∴x+100=150．‎ 答：乙工程队每天修‎100米，则甲工程队每天修‎150米．‎ ‎21、（2011•曲靖）在三张完全相同的卡片上分别标注：A“雨水”、B“大地”、C“生机”，放入一个不透明的的口袋中，随机从中抽出一张放入“给带来”左边“”内；第二次抽出一张放入中间的“”内；第三次抽出一张放入右边的“”内（每次卡片抽出后不放回）．‎ ‎（1）试用树形图列出三次抽卡出现的所有可能的结果；‎ ‎（2）求其中恰好组成“雨水给大地带来生机”的概率．‎ 解答：解：（1）；‎ ‎（2）共6种情况，“雨水给大地带来生机”的情况数有1种，所以概率为．‎ ‎22、（2011•曲靖）一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是，铅球运行路线如图．‎ ‎（1）求铅球推出的水平距离；‎ ‎（2）通过计算说明铅球行进高度能否达到‎4m．‎ 解答：解：（1）当y=0时，﹣x2+x+=0，‎ 解之得x1=10，x2=﹣2（不合题意，舍去），‎ 所以推铅球的成绩是‎10米．‎ ‎（2）=﹣（x2﹣8x+16）++‎ ‎=﹣（x﹣4）2+3，‎ 当x=4时，y取最大值3，‎ 所以铅球行进高度不能达到‎4m，最高能达到‎3m．‎ ‎23、（2011•曲靖）如图，点A、B、C、D都在⊙O上，OC⊥AB，∠ADC=30°．‎ ‎（1）求∠BOC的度数；‎ ‎（2）求证：四边形AOBC是菱形．‎ 解答：解：（1）∵点A、B、C、D都在⊙O上，OC⊥AB，‎ ‎∴=，‎ ‎∵∠ADC=30°，‎ ‎∴∠AOC=∠BOC=2∠ADC=60°，‎ ‎∴∠BOC的度数为60°；‎ ‎（2）证明：∵=，‎ ‎∴AC=BC，‎ AO=BO，‎ ‎∵∠BOC的度数为60°，‎ ‎∴△BOC为等边三角形，‎ ‎∴BC=BO=CO，‎ ‎∴AO=BO=AC=BC，‎ ‎∴四边形AOBC是菱形．‎ ‎24、（2011•曲靖）如图：直线y=kx+3与x轴、y轴分别交于A、B两点，tan∠OAB=，点C（x，y）是直线y=kx+3上与A、B不重合的动点．‎ ‎（1）求直线y=kx+3的解析式；‎ ‎（2）当点C运动到什么位置时△AOC的面积是6；‎ ‎（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由．‎ 解答：解：（1）∵直线y=kx+3与y轴分别交于B点，‎ ‎∴B（0，3），‎ ‎∵tan∠OAB=，‎ ‎∴OA=4，‎ ‎∴A（4，0），‎ ‎∵直线y=kx+3过A（4，0），‎ ‎∴4k+3=0，‎ ‎∴k=﹣，‎ ‎∴直线的解析式为：y=﹣x+3；‎ ‎（2）∵A（4，0），‎ ‎∴AO=4，‎ ‎∵△AOC的面积是6，‎ ‎∴△AOC的高为：3，‎ ‎∴C点的纵坐标为3，‎ ‎∵直线的解析式为：y=﹣x+3，∴3=﹣x+3， ∴x=0，‎ ‎∴点C运动到B点时，△AOC的面积是6；‎ ‎（3）当过点C的另一直线CD与y轴相交于D点，‎ 且CD⊥y轴于点D时，BD=BO=3，△BCD与△AOB全等，‎ ‎， ‎ ‎∴6=﹣x+3，‎ 解得：x=﹣4，‎ ‎∴C点坐标为：（﹣4，6）．‎