- 2021-05-25 发布 |
- 37.5 KB |
- 5页

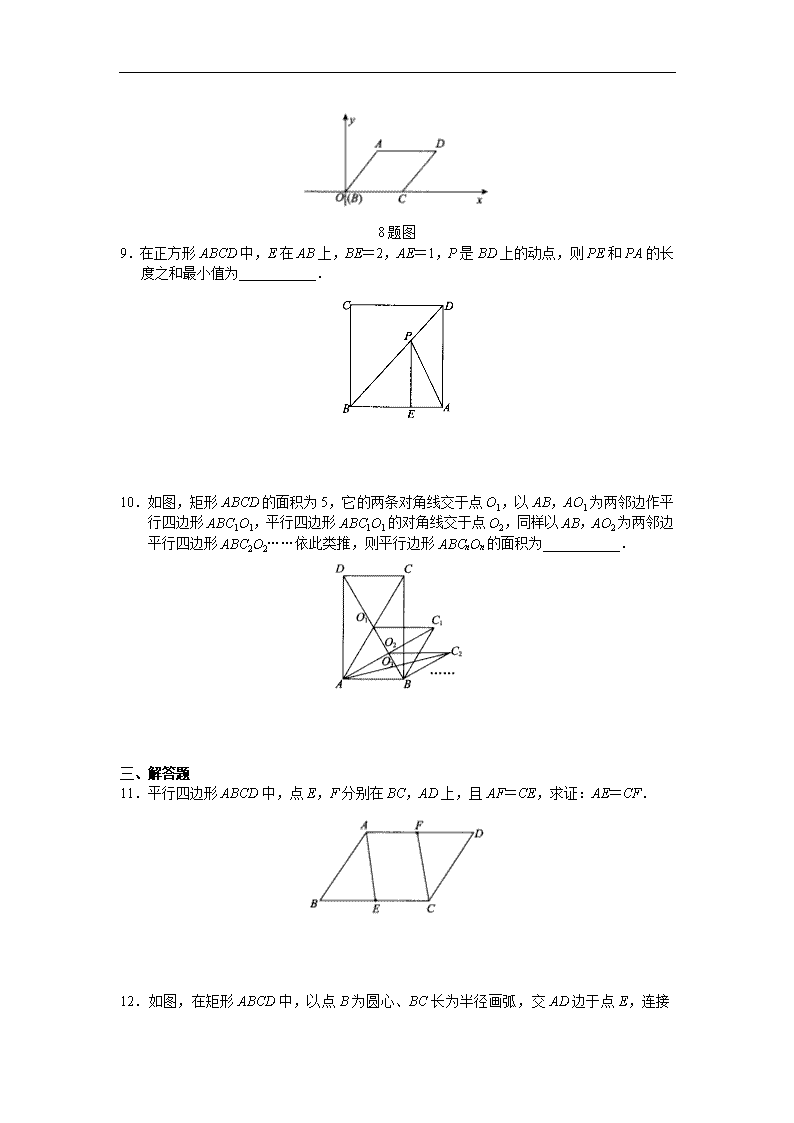
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版数学八下第十八章《平行四边形》单元测试
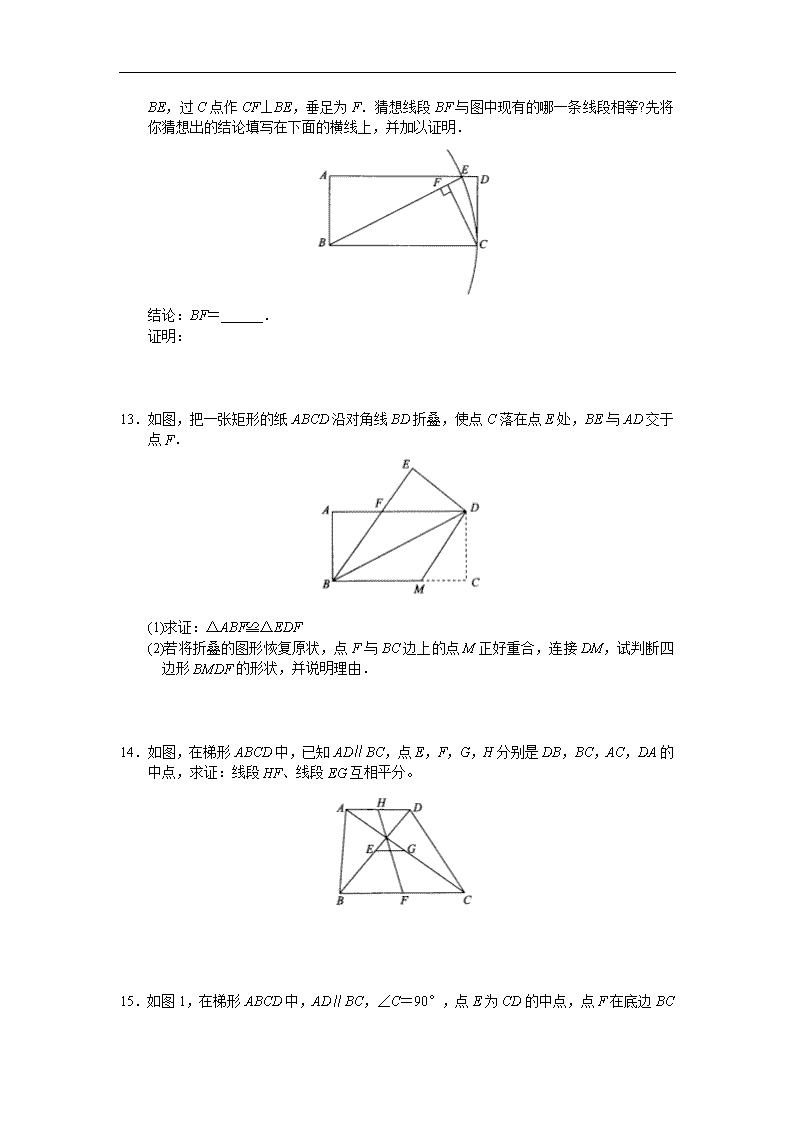
第十八章 平行四边形全章测试 一、选择题 1.下列说法中,正确的是( ). (A)等腰梯形既是中心对称图形又是轴对称图形. (B)平行四边形的邻边相等. (C)矩形是轴对称图形且有四条对称轴. (D)菱形的面积等于两条对角线长乘积的一半. 2.在□ABCD 中,AB=3cm,AD=4cm,∠A=120°,则□ABCD 的面积是( ). (A) 33 (B) 36 (C) 315 (D) 312 3.将矩形纸片 ABCD 按如图所示的方式折叠,得到菱形 AECF.若 AB=3,则 BC 的长 为( ). (A)1 (B)2 (C) 2 (D) 3 4.等腰梯形的两底之差等于腰长,则腰与下底的夹角为( ). (A)120° (B)60° (C)45° (D)50° 5.课外活动时,王老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为 450cm2,则两条对角线所用的竹条至少需( ). (A) cm230 (B)30cm (C)60cm (D) cm260 二、填空题 6.如图,若□ABCD 与□EBCF 关于 B,C 所在直线对称,∠ABE=90°,则∠F=______. 7.已知菱形 ABCD 的面积是 12cm2,对角线 AC=4cm,则菱形的边长是______cm. 8.如图,菱形 ABCD 的边长为 2,∠ABC=45°,则点 D 的坐标为______. 8 题图 9.在正方形 ABCD 中,E 在 AB 上,BE=2,AE=1,P 是 BD 上的动点,则 PE 和 PA 的长 度之和最小值为___________. 10.如图,矩形 ABCD 的面积为 5,它的两条对角线交于点 O1,以 AB,AO1 为两邻边作平 行四边形 ABC1O1,平行四边形 ABC1O1 的对角线交于点 O2,同样以 AB,AO2 为两邻边 平行四边形 ABC2O2……依此类推,则平行边形 ABCnOn 的面积为___________. 三、解答题 11.平行四边形 ABCD 中,点 E,F 分别在 BC,AD 上,且 AF=CE,求证:AE=CF. 12.如图,在矩形 ABCD 中,以点 B 为圆心、BC 长为半径画弧,交 AD 边于点 E,连接 BE, 过 C 点作 CF⊥BE,垂足为 F.猜想线段 BF 与图中现有的哪一条线段相等?先将你猜想 出的结论填写在下面的横线上,并加以证明. 结论:BF=______. 证明: 13.如图,把一张矩形的纸 ABCD 沿对角线 BD 折叠,使点 C 落在点 E 处,BE 与 AD 交于 点 F. (1)求证:△ABF≌△EDF (2)若将折叠的图形恢复原状,点 F 与 BC 边上的点 M 正好重合,连接 DM,试判断四 边形 BMDF 的形状,并说明理由. 14.如图,在梯形 ABCD 中,已知 AD∥BC,点 E,F,G,H 分别是 DB,BC,AC,DA 的 中点,求证:线段 HF、线段 EG 互相平分。 15.如图 1,在梯形 ABCD 中,AD∥BC,∠C=90°,点 E 为 CD 的中点,点 F 在底边 BC 上,且∠FAE=∠DAE. 图 1 (1)请你通过观察、测量、猜想,写出∠AEF 的度数; (2)若梯形 ABCD 中,AD∥BC,∠C 不是直角,点 F 在底边 BC 或其延长线上,如图 2、图 3,其他条件不变,你在(1)中得出的结论是否仍然成立,若都成立,请在 图 2、图 3 中选择其中一图进行证明;若不都成立,请说明理由. 图 2 图 3 16.如图 1,P 是线段 AB 上的一点,在 AB 的同侧作△APC 和△BPD,使 PC=PA,PD= PB,∠APC=∠BPD,连结 CD,点 E,F,G,H 分别是 AC,AB,BD,CD 的中点, 顺次连接 E,F,G,H. 图 1 (1)猜想四边形 EFGH 的形状,直接回答,不必说明理由; (2)当点 P 在线段 AB 的上方时,如图 2,在△APB 的外部作△APC 和△BPD,其他条件 不变,(1)中的结论还成立吗?说明理由; 图 2 (3)如图 3 中,若∠APC=∠BPD=90°,其他条件不变,先补全图 3,再判断四边形 EFGH 的形状,并说明理由. 图 3 参考答案 第十八章 平行四边形全章测试 1.D. 2.B. 3.D. 4.B. 5.C. 6.45. 7. .13 8. ).2,22( 9. .13 10. n2 5 11.略. 12.BF=AE;证明提示:△BAE≌△CFB. 13.(1)略;(2)菱形. 14.提示:连结 EH,HG,GF,FE 15.(1)90°;(2)提示:延长 AE 与 BC 延长线交于点 G,证明△AFG 是等腰三角形; 16.(1)菱形; (2)菱形,提示:连结 CB,AD;证明 CB=AD; (3)如图,正方形,提示:连结 CB、AD,证明△APD≌△CPB,从而得出 AD=CB, ∠DAP=∠BCP,进而得到 CB⊥AD.查看更多