- 2021-05-25 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题四边形复习练习含答案
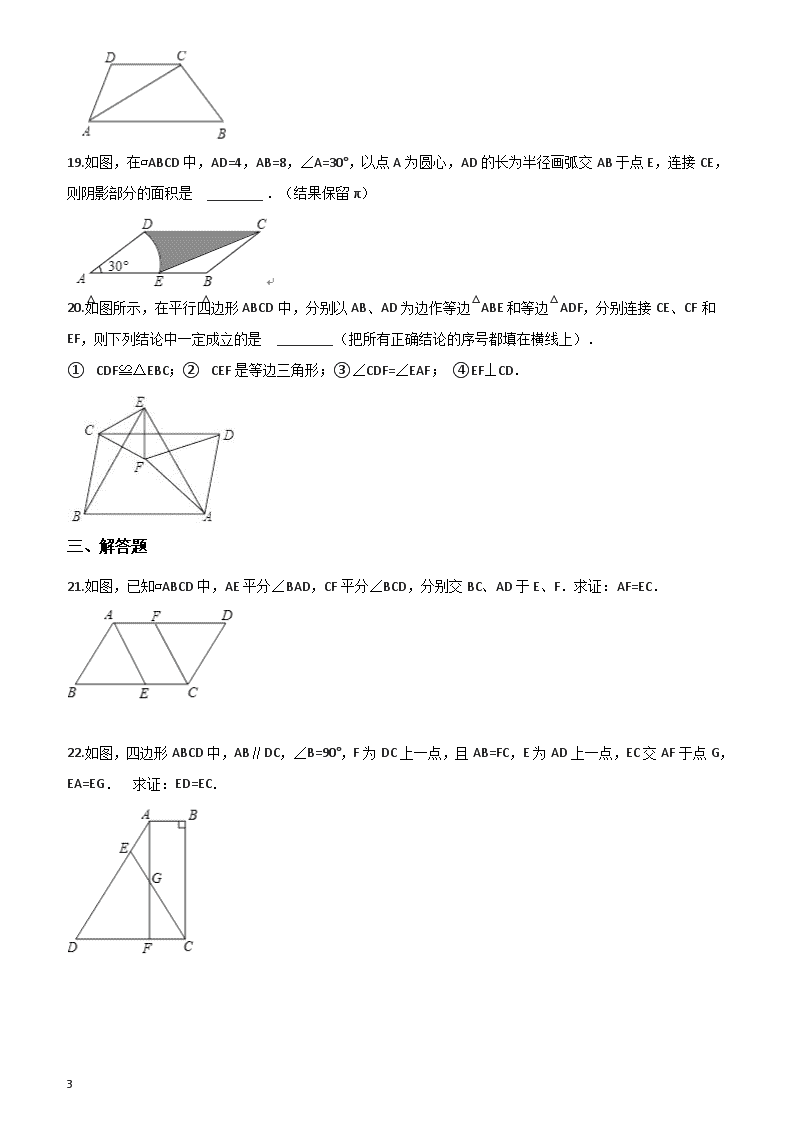
四边形 一、选择题 1.下列命题中,不正确的是( ). A. 平行四边形的对角线互相平分 B. 矩形的对角线互相垂直且平分 C. 菱形的对角线互相垂直且平分 D. 正方形的对角线相等且互相垂直平分 2.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形. A. 6 B. 5 C. 8 D. 7 3.如图,在▱ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( ) A. 45° B. 55° C. 65° D. 75° 4.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为( ) A. 13 B. 15 C. 13或15 D. 15或16或17 5.如图,若要使平行四边形ABCD成为菱形.则需要添加的条件是( ) A. AB=CD B. AD=BC C. AB=BC D. AC=BD 6.如下图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB长为( ) A. 20 B. 15 C. 10 D. 5 7.如图,在□ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有 ( ) A. 7 个 B. 8个 C. 9个 D. 11个 8.如图,在七边形ABCDEFG中,AB,ED的延长线相交于O点.若图中 10 ∠1,∠2,∠3,∠4的角度和为220°,则∠BOD的度数为( ) A. 40° B. 45° C. 50° D. 60° 9.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( ) A. 6cm B. 5cm C. cm D. 7.5cm 10.能够铺满地面的正多边形组合是( ) A. 正三角形和正五边形 B. 正方形和正六边形 C. 正方形和正五边形 D. 正五边形和正十边形 二、填空题 11.一个多边形对角线的数目是边数的2倍,这样的多边形的边数是________ . 12.如图,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是________ 13.已知平行四边形ABCD中,AB=5,AE平分∠DAB交BC所在直线于点E,CE=2,则AD=________. 14.如图:矩形ABCD的对角线相交于点O,AB=4cm,∠AOB=60°,则AD=________ cm. 15.八年级(3班)同学要在广场上布置一个矩形花坛,计划用鲜花摆成两条对角线.如果一条对角线用了20盆红花,还需要从花房运来________盆红花.如果一条对角线用了25盆红花,还需要从花房运来________盆红花. 16.在正三角形、正方形、正五边形、正六边形中不能镶嵌成一个平面图案的是________ . 17.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为________cm2 . 18.梯形ABCD的底AB的长度等于底CD的2倍,也等于腰AD的2倍,设对角线AC的长为3,腰BC的长为4,则梯形ABCD的高为________. 10 19.如图,在▱ABCD中,AD=4,AB=8,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 ________ .(结果保留π) 20.如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是 ________ (把所有正确结论的序号都填在横线上). ①△CDF≌△EBC;②△CEF是等边三角形;③∠CDF=∠EAF; ④EF⊥CD. 三、解答题 21.如图,已知▱ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC. 22.如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG. 求证:ED=EC. 10 23.如图,平行四边形ABCD的对角线AC和BD相交于点O , E , F分别为OB , OD的中点,过点O任作一直线分别交AB , CD于点G , H. 试说明:GF∥EH. 24.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC. (1)求证:BE=AF; (2)若∠ABC=60°,BD=12,求DE的长及四边形ADEF的面积. 25.如图,正方形ABCD的边长为8cm,E、F、G分别是AB、CD、DA上的动点,且AE=BF=CG=DH. (1)求证:四边形EFGH是正方形; (2)判断直线EG是否经过某一定点,说明理由; (3)求四边形EFGH面积的最小值. 10 26.如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. (1)如果∠B+∠C=120°,则∠AED的度数=________.(直接写出结果) (2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明. 27.如图1,△ABD和△BDC都是边长为1的等边三角形。 (1)四边形ABCD是菱形吗?为什么? (2)如图2,将△BDC沿射线BD方向平移到△B1D1C1的位置,则四边形ABC1D1 是平行四边形吗?为什么? (3)在△BDC移动过程中,四边形ABC1D1有可能是矩形吗?如果是,请在图3中画出四边形ABC1D1为矩形时的图形,并直接写出点B移动的距离(不要求写出过程);如果不是,请说明理由。 10 参考答案 一、选择题 1.B 2. B 3. A 4. D 5. C 6.D 7. C 8. A 9.B 10. D 二、填空题 11.7 12.BE=DF(答案不唯一) 13.3或7 14.4 15.19;24 16.正五边形 17.96cm2 18. 19.12﹣π 20.①②③ 三、解答题 21.证明:∵四边形ABCD为平行四边形, ∴AD∥BC∠BAD=∠BCD, ∴AF∥EC, ∴∠DAE=∠AEB, ∵AE平分∠BAD,CF平分∠BCD, ∴∠DAE=∠BAD,∠FCB=∠BCD, ∴∠DAE=∠FCB=∠AEB, ∴AE∥FC, ∴四边形AECF为平行四边形, ∴AF=CE 22.解:证明:∵AB∥DC,FC=AB, ∴四边形ABCF是平行四边形. ∵∠B=90°, ∴四边形ABCF是矩形. ∴∠AFC=90°, ∴∠D=90°﹣∠DAF,∠ECD=90°﹣∠CGF. ∵EA=EG, ∴∠EAG=∠EGA. ∵∠EGA=∠CGF, ∴∠DAF=∠CGF. ∴∠D=∠ECD. ∴ED=EC 10 23.证明:连结EG , FH , 由□ABCD得 OA=OC , OB=OD , 又OE= OB , OF= OD , ∴OE=OF , 再证△AOG≌△COH得OG=OH , ∴四边形EHFG是平行四边形, ∴GF∥EH. 24.(1)证明:∵DE∥AB,EF∥AC, ∴四边形ADEF是平行四边形, ∠ABD=∠BDE, ∴AF=DE, ∵BD是△ABC的角平分线, ∴∠ABD=∠DBE, ∴∠DBE=∠BDE, ∴BE=DE, ∴BE=AF; (2)解:如图,过点D作DG⊥AB于点G,过点E作EH⊥BD于点H, ∵∠ABC=60°,BD是∠ABC的平分线, ∴∠ABD=∠EBD=30°, ∴DG=BD=×12=6, ∵BE=DE, ∴BH=DH=BD=6, ∴BE==. ∴DE=BE=, 10 ∴四边形ADEF的面积为:DE•DG=. 25.(1)证明:∵四边形ABCD是正方形, ∴∠A=∠B=90°, AB=DA, ∵AE= DH, ∴BE= AH, ∴△AEH≌△BFE, ∴EH=FE,∠AHE=∠BEF, 同理:FE=GF=HG, ∴EH= FE=GF=HG, ∴四边形EFGH是菱形, ∵∠A=90°, ∴∠AHE+∠AEH=90°, ∴∠BEF+∠AEH=90°, ∴∠FEH=90°, ∴菱形EFGH是正方形; (2)解:直线EG经过正方形ABCD的中心, 理由如下:连接BD交EG于点O, ∵四边形ABCD是正方形, ∴AB∥DC,AB=DC 10 ∴∠EBD=∠GDB, ∵AE= CG, ∴BE= DG, ∵∠EOB=∠GOD, ∴△EOB≌△GOD, ∴BO=DO,即点O为BD的中点, ∴直线EG经过正方形ABCD的中心; (3)解:设AE= DH=x, 则AH=8-x, 在Rt△AEH中,EH2=AE2+AH2=x2+(8-x)2= 2x2-16x+64=2(x-4)2+32, ∴四边形EFGH面积的最小值为32cm². 26.(1)60° (2)解:∠AED= (∠B+∠C). 理由如下:在四边形ABCD中, ∵∠BAD+∠CDA+∠B+∠C=360°, ∴∠BAD+∠CDA=360°﹣(∠B+∠C), 又∵AE平分∠BAD,DE平分∠ADC, ∴∠EAD= ∠BAD,∠EDA= ∠ADC, ∴∠EAD+∠EDA= ∠BAD+ ∠ADC= [360°﹣(∠B+∠C)], 在△AED中,又∵∠AED=180°﹣(∠EAD+∠EDA), =180°﹣ [360°﹣(∠B+∠C)], = (∠B+∠C), 故∠AED= (∠B+∠C). 27.(1)解:四边形ABCD是菱形 理由如下: ∵△ABD和△BDC都是边长为1的等边三角形。 ∴AB=AD=CD=BC=DB, ∴AB=AD=CD=BC, ∴四边形ABCD是菱形 (2)解:四边形ABC1D1是平行四边形 10 理由:∵∠ABD =∠ =60° ∴AB∥ 新网 又∵AB= , ∴四边形 是平行四边形 (3)解:四边形 有可能是矩形 点B移动的距离是1 10查看更多