- 2021-05-25 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙教版八年级上册数学同步课件-第1章-1三角形的初步认识
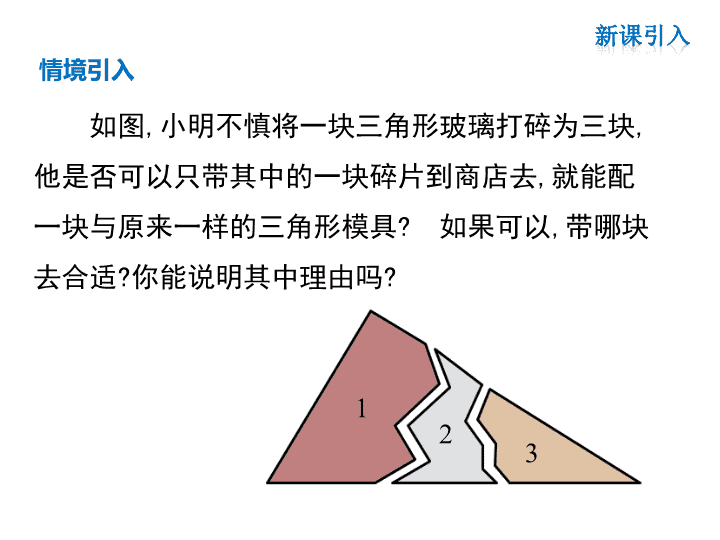
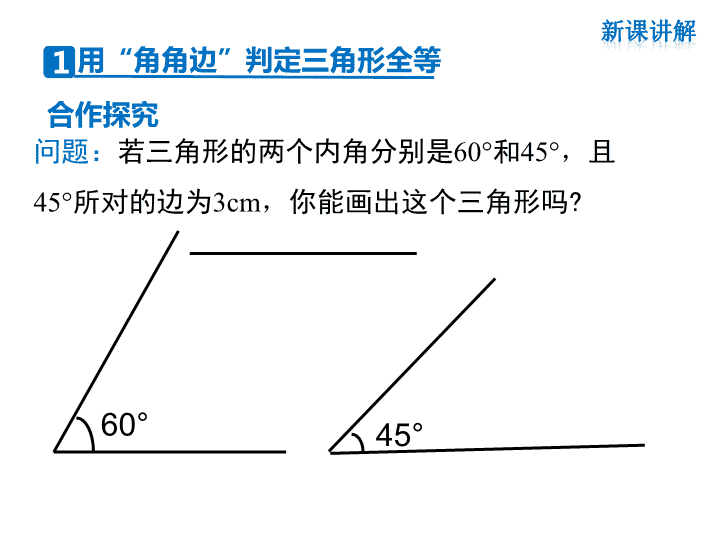
第4课时 角角边及角平分线的性质 1.5 全等三角形的判定 第1章 三角形的初步认识 如图,小明不慎将一块三角形玻璃打碎为三块, 他是否可以只带其中的一块碎片到商店去,就能配 一块与原来一样的三角形模具? 如果可以,带哪块 去合适?你能说明其中理由吗? 情境引入 3 2 1 问题:若三角形的两个内角分别是60°和45°, 且45°所对的边为3cm,你能画出这个三角形吗? 60° 45° 用“角角边”判定三角形全等 合作探究 1 60° 45° 思考: 这里的条件与1中的条件有什么相同点与不同点? 你能将它转化为1中的条件吗? 75° 两角和其中一角的对边对应相等的两个三角形全等. 简写成“角角边”或“AAS”. 归纳总结 ∠A=∠A′, ∠B=∠B′ , AC=A′C ′, 在△ABC和△A′B′C′中, ∴ △ABC≌△ A′ B′ C′ (AAS). A B C A ′ B ′ C ′ 例3:在△ABC和△DEF中,∠A=∠D,∠B= ∠E, BC=EF.求证:△ABC≌△DEF. ∠B=∠E, BC=EF, ∠C=∠F. 证明:在△ABC中,∠A+∠B+∠C=180°. ∴△ABC≌△DEF(ASA ). ∴ ∠C=180°-∠A-∠B. 同理 ∠F=180°-∠D-∠E. 又 ∠A=∠D,∠B= ∠E, ∴ ∠C=∠F. 在△ABC和△DEF中, 例4 如图,已知:在△ABC中,∠BAC=90°, AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线 m,垂足分别为点D、E. 求证:(1)△BDA≌△AEC; 证明:(1)∵BD⊥m,CE⊥m, ∴∠ADB=∠CEA=90°, ∴∠ABD+∠BAD=90°. ∵AB⊥AC, ∴∠BAD+∠CAE=90°, ∠ABD=∠CAE. 在△BDA和△AEC中, ∠ADB=∠CEA=90°, ∠ABD=∠CAE, AB=AC, ∴△BDA≌△AEC(AAS). (2)DE=BD+CE. ∴BD=AE,AD=CE, ∴DE=DA+AE=BD+CE. 证明:∵△BDA≌△AEC, 方法总结:利用全等三角形可以解决线段之间的关系, 比如线段的相等关系、和差关系等,解决问题的关键是 运用全等三角形的判定与性质进行线段之间的转化. 角平分线的性质定理 如图,点P是∠AOB的角平分线OC上的任意一点,且 PD⊥OA于点D,PE⊥OB于点E,将∠AOB沿OC对折,你 发现了什么?如何表达,并简述你的证明过程. 对折后PD、PE能够完全重合,PD=PE. 角是轴对称图形吗?它的对称轴是什么? D P A C BEO 2 下面我们来证明刚才得到的结论. D P A C BEO 已知:OC平分∠AOB, P是OC上任意一点,PD⊥OA,PE⊥OB . 求证:PD=PE. 证明:∵ OC平分∠AOB, P是OC上一点, ∴∠DOP=∠BOP. ∵PD⊥OA,PE⊥OB , ∴∠ODP=∠OEP=90°. 在△OPD和△OPE 中, ∵ ∠DOP=∠EOP ,∠ODP=∠OEP ,OP=OP, ∴ △OPD≌△OPE (A.A.S.). ∴PD=PE(全等三角形的对应边相等). 由上面证明,我们得到角平分线的性质定理: 角平分线上的点到角两边的距离相等. 几何语言描述:∵ OC平分∠AOB, 且PD⊥OA, PE⊥OB. ∴ PD= PE. 应用所具备的条件: (1)角的平分线; (2)点在该平分线上; (3)垂直距离. 定理的作用: 证明线段相等. 1.如图, DE⊥AB, DF⊥BC, 垂足分别是E、 F, DE =DF, ∠EDB= 60°, 则 ∠EBF= ,BE= .60° BF A B C D E F A B C D E F 2.如图∠ACB=∠DFE,BC=EF,那么应补充一 个条件 ,才能使△ABC≌△DEF (写出一个即可). ∠B=∠E 或∠A=∠D 或 AC=DF (ASA) (AAS) (SAS) AB=DE可以吗?× AB∥DE 3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证: AB=AD. A C DB 1 2证明: ∵ AB⊥BC,AD⊥DC, ∴ ∠ B=∠D=90 °. 在△ABC和△ADC中, ∠1=∠2 , ∠ B=∠D, AC=AC , ∴ △ABC≌△ADC(AAS), ∴AB=AD. 角 角 边 内 容 应 用 角平分线 的性质 性质定理:角平分线上的点 到角两边的距离相等查看更多