【数学】2019届一轮复习人教A版高考解答题专项突破-概率统计分布列学案

【数学】2019届一轮复习人教A版高考解答题专项突破-概率统计分布列学案

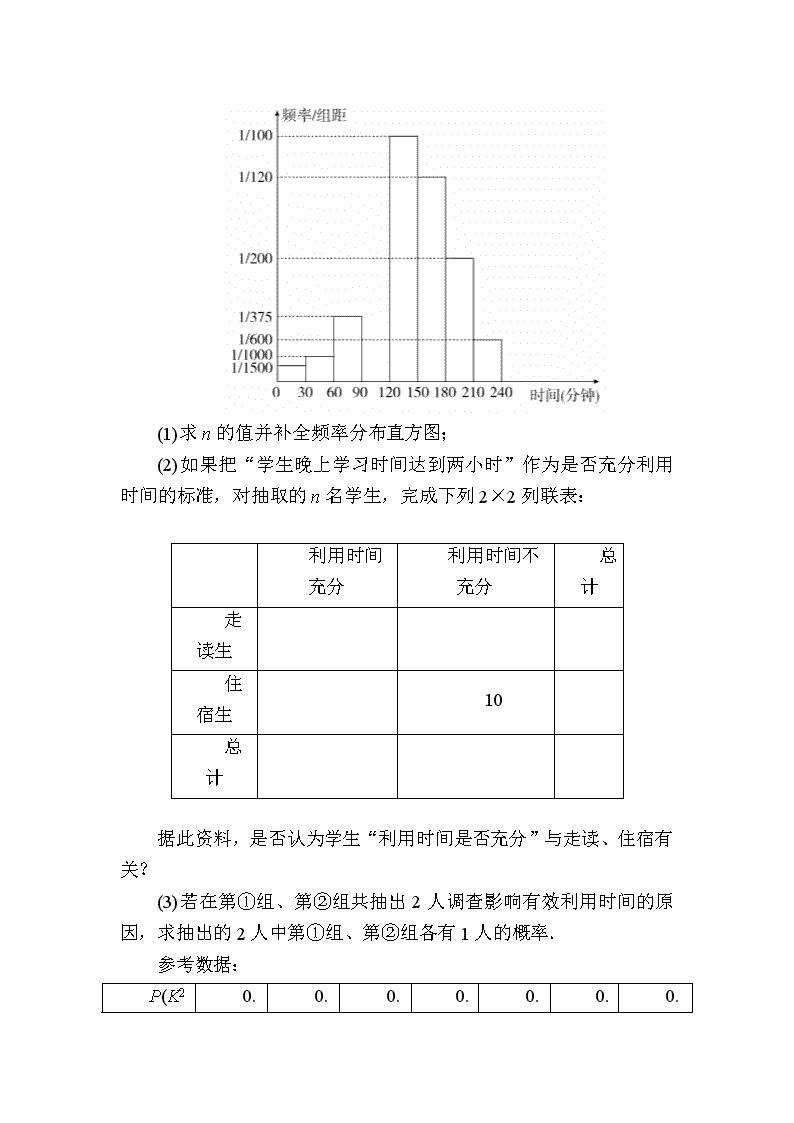
热点题型1　统计与统计案例 以实际生活中的事例为背景，通过对相关数据的分析进行统计、抽象概括，做出估计与判断．常与抽样方法、频率分布直方图、茎叶图、概率等知识交汇考查，考查考生的数据处理能力和运算求解能力．‎ 　　(2018·合肥质检)为了调查学生星期天晚上学习时间的利用问题，某校从高二年级1000名学生(其中走读生450名，住宿生550名)中，采用分层抽样的方法抽取n名学生进行问卷调查．根据问卷取得了这n名同学星期天晚上学习时间(单位：分钟)的数据，按照以下区间分为八组：①[0,30)，②[30,60)，③[60,90)，④[90，120)，⑤[120,150)，⑥[150,180)，⑦[180,210)，⑧[210,240)，得到频率分布直方图如图．已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人．‎ ‎(1)求n的值并补全频率分布直方图；‎ ‎(2)如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准，对抽取的n名学生，完成下列2×2列联表：‎ 利用时间充分 利用时间不充分 总计 走读生 住宿生 ‎10‎ 总计 据此资料，是否认为学生“利用时间是否充分”与走读、住宿有关？‎ ‎(3)若在第①组、第②组共抽出2人调查影响有效利用时间的原因，求抽出的2人中第①组、第②组各有1人的概率．‎ 参考数据：‎ P(K2‎ ‎0.‎ ‎0.‎ ‎0.‎ ‎0.‎ ‎0.‎ ‎0.‎ ‎0.‎ ‎≥k0)‎ ‎15‎ ‎10‎ ‎05‎ ‎025‎ ‎010 ‎ ‎005‎ ‎001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参考公式：K2＝，其中n＝a＋b＋c＋d.‎ 解　(1)设第i组的频率为Pi(i＝1,2，…，8)，‎ 由图可知P1＝×30＝，P2＝×30＝，‎ ‎∴学习时间少于60分钟的频率为P1＋P2＝，‎ 由题意得n×＝5，∴n＝100.‎ 又P3＝×30＝，P5＝×30＝，‎ P6＝×30＝，P7＝×30＝，‎ P8＝×30＝，‎ ‎∴P4＝1－(P1＋P2＋P3＋P5＋P6＋P7＋P8)＝，‎ ‎∴第④组的高度为h＝×＝＝，‎ 频率分布直方图如图．‎ ‎(2)由频率分布直方图可知，在抽取的100人中，“住宿生”有55人，“走读生”有45人，利用时间不充分的有100×(P1＋P2＋P3＋P4)＝25(人)，‎ 从而2×2列联表如下：‎ 利用时间充分 利用时间不充分 总计 走读生 ‎ 30‎ ‎15‎ ‎45‎ 住宿生 ‎ 45‎ ‎10‎ ‎55‎ 总计 ‎ 75‎ ‎ 25‎ ‎100‎ 将2×2列联表中的数据代入公式计算，‎ 得K2＝ ‎＝ ‎＝≈3.030.‎ ‎∵3.030<3.841，‎ ‎∴没有理由认为学生“利用时间是否充分”与走读、住宿有关．‎ ‎(3)由题可知第①组人数为100×P1＝2(人)，第②组人数为100×P2＝3(人)，‎ 记第①组的2人为A1，A2，第②组的3人为B1，B2，B3，‎ 则“从5人中抽取2人”所构成的基本事件有A‎1A2，A1B1，A1B2，A1B3，A2B1，A2B2，A2B3，B1B2，B1B3，B2B‎3”‎，共10个基本事件；‎ 记“抽取2人中第①组、第②组各有1人”记作事件A，则事件A所包含的基本事件有A1B1，A1B2，A1B3，A2B1，A2B2，A2B3，共6个基本事件，‎ ‎∴P(A)＝＝，‎ 即抽出的2人中第①组、第②组各有1人的概率为.‎ 热点题型2　概率与统计的综合 以实际问题为背景，利用频率估计概率，常与抽样方法、茎叶图、频率分布直方图、概率及其分布列等知识交汇命题，考查考生分析问题及解决问题的能力．‎ 　　(2017·江西新余模拟)‎2016年10月21日，台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾，某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失，将收集的数据(单位：元)分成[0,2000]，(2000,4000]，(4000,6000]，(6000,8000]，(8000,10000]五组，并作出如图所示的频率分布直方图．‎ ‎(1)台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如下表所示，在表格空白处填写正确数字，并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自家经济损失是否超过4000元有关；‎ ‎(2)将上述调查所得到的频率视为概率，现在从该地区大量受灾居民中，采用随机抽样的方法每次抽取1户居民，抽取3次，记抽取的3户居民中自家经济损失超过4000元的户数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列、期望E(ξ)和方差D(ξ)．‎ K2＝.‎ 解　(1)由频率分布直方图可得，在抽取的100户中，经济损失不超过4000元的有70户，经济损失超过4000元的有30户，补全表格数据如下：‎ 则K2＝≈4.762.‎ 因为4.762>3.841.‎ 所以可以在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自家经济损失是否超过4000元有关．‎ ‎(2)由频率分布直方图可知抽到自家经济损失超过4000元的居民的频率为0.3，将频率视为概率，由题意知ξ的可能取值为0,1,2,3，且ξ～B，‎ P(ξ＝0)＝C03＝，‎ P(ξ＝1)＝C12＝，‎ P(ξ＝2)＝C21＝，‎ P(ξ＝3)＝C30＝.‎ 从而ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P E(ξ)＝np＝3×＝0.9，D(ξ)＝np(1－p)＝3××＝0.63.‎ 热点题型3　离散型随机变量的分布列、期望与方差 离散型随机变量分布列及均值与方差及其应用是高考中的一个热点．解题时要弄清离散型随机变量的所有取值及每个取值下对应的概率，对概型的确定及转化是解题的关键．‎ 　　(2017·河南质监)小李参加一种红包接龙游戏：他在红包里塞了12元，然后发给朋友A，如果A猜中，A将获得红包里的所有金额；如果A未猜中，A将当前的红包转发给朋友B，如果B猜中，A、B平分红包里的金额；如果B未猜中，B将当前的红包转发给朋友C，如果C猜中，A、B和C平分红包里的金额；如果C未猜中，红包里的钱将退回小李的帐户，设A、B、C猜中的概率分别为，，，且A、B、C是否猜中互不影响．‎ ‎(1)求A恰好获得4元的概率；‎ ‎(2)设A获得的金额为X元，求X的分布列；‎ ‎(3)设B获得的金额为Y元，C获得的金额为Z元，判断A所获得的金额的期望能否超过Y的期望与Z的期望之和．‎ 解　(1)A恰好获得4元的概率为××＝.‎ ‎(2)X的可能取值为0,4,6,12，‎ P(X＝4)＝，P(X＝0)＝××＝，‎ P(X＝6)＝×＝，P(X＝12)＝，‎ 所以X的分布列为：‎ X ‎0‎ ‎4‎ ‎6‎ ‎12‎ P ‎(3)Y的可能取值为0,4,6；Z的可能取值为0,4.‎ 因为P(Y＝0)＝＋××＝，‎ P(Y＝4)＝××＝，‎ P(Y＝6)＝×＝，‎ P(Z＝0)＝＋×＋××＝，‎ P(Z＝4)＝××＝，‎ 所以E(Y)＝0×＋4×＋6×＝，‎ E(Z)＝0×＋4×＝，‎ 所以E(Y)＋E(Z)＝，‎ 又E(X)＝0×＋4×＋6×＋12×＝，‎ 由于E(X)>E(Y)＋E(Z)，所以A所获得的金额的期望能超过Y的期望与Z的期望之和．‎ 热点题型4　样本数字特征与正态分布的综合 样本的数字特征与正态分布及概率分布列的综合在高考中时有出现，体现了知识网络的交汇，命题新颖，具有一定的创新性．解决与正态分布有关的问题重在理解μ，σ2的意义及密度曲线的对称性．‎ 　　(2017·全国卷Ⅰ)为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸(单位：cm)．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ，σ2)．‎ ‎(1)假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在(μ－3σ，μ＋3σ)之外的零件数，求P(X≥1)及X的数学期望；‎ ‎(2)一天内抽检零件中，如果出现了尺寸在(μ－3σ，μ＋3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．‎ ‎①试说明上述监控生产过程方法的合理性；‎ ‎②下面是检验员在一天内抽取的16个零件的尺寸：‎ 经计算得＝i＝9.97，s＝＝≈0.212，其中xi为抽取的第i个零件的尺寸，i＝1,2，…，16.‎ 用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对当天的生产过程进行检查．剔除(－3，＋3)之外的数据，用剩下的数据估计μ和σ(精确到0.01)．‎ 附：若随机变量Z服从正态分布N(μ，σ2)，则P(μ－3σ

查看更多