【数学】2020届一轮复习人教A版第十四章空间向量第4课　空间向量的共线与共面学案（江苏专用）

【数学】2020届一轮复习人教A版第十四章空间向量第4课　空间向量的共线与共面学案（江苏专用）

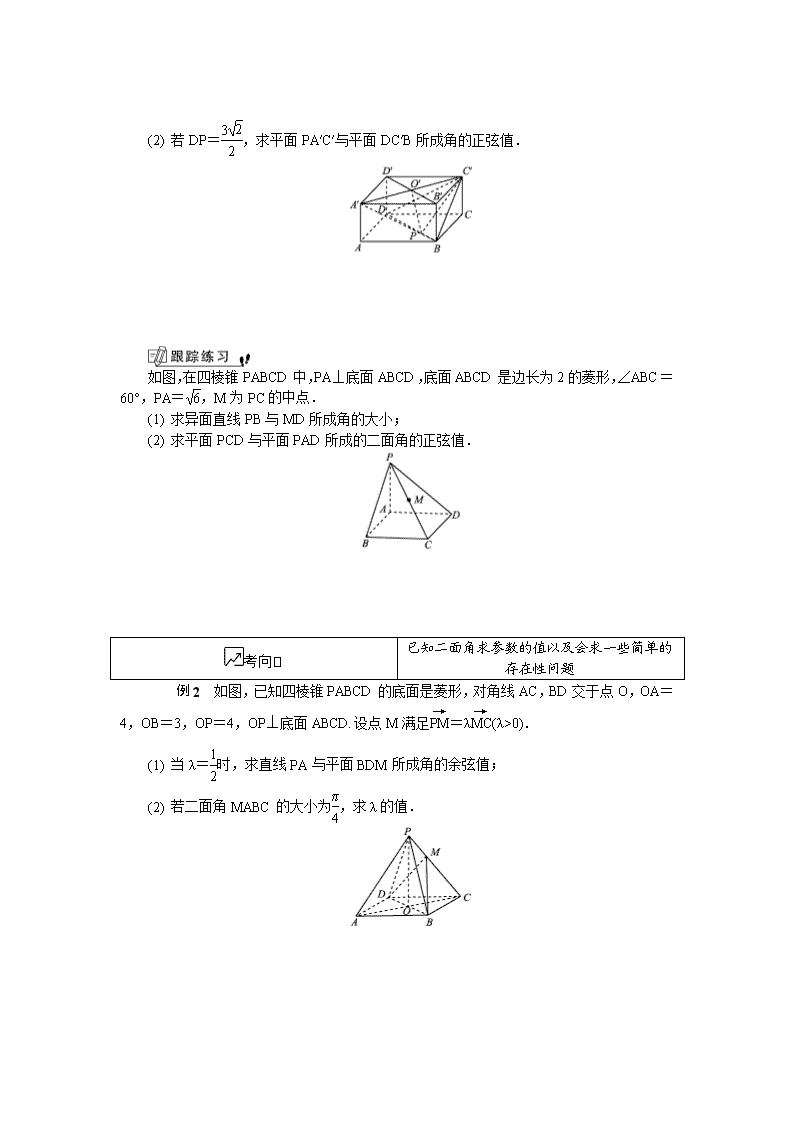
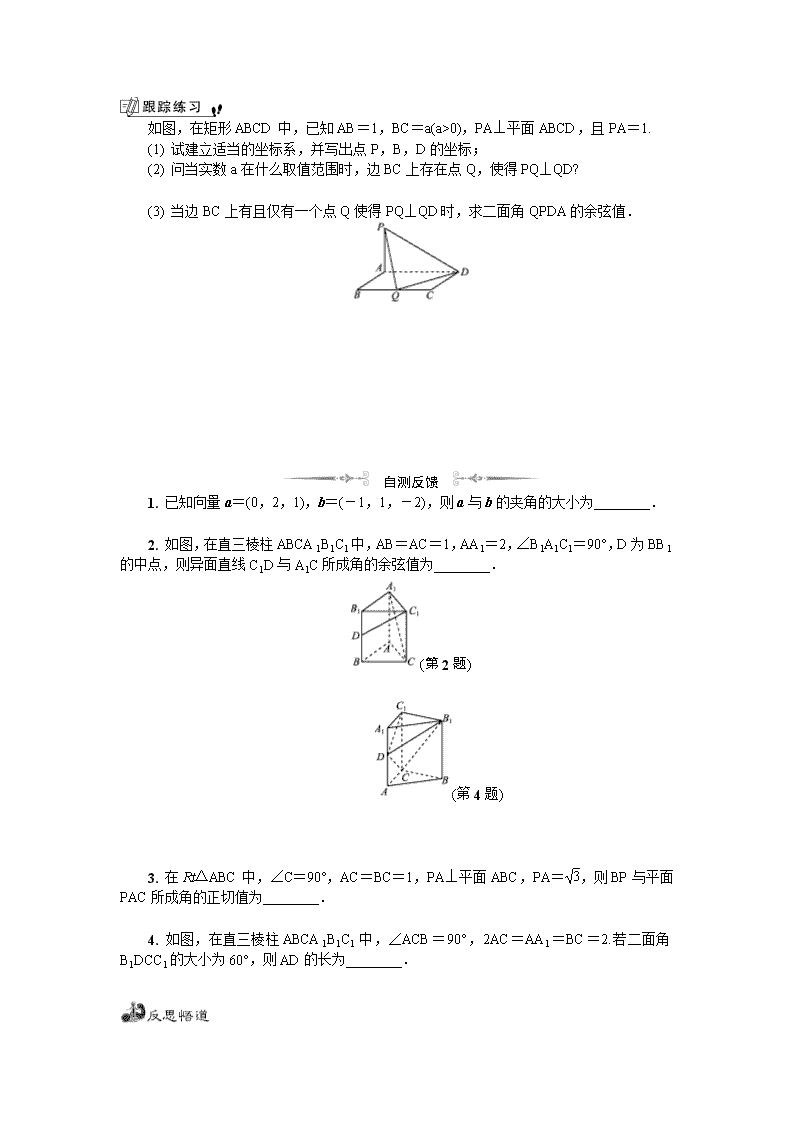
第4课__空间向量的共线与共面____‎ ‎1. 理解直线的方向向量，会用待定系数法求平面的法向量．‎ ‎2. 会用两直线方向向量的夹角，直线方向向量与平面法向量的夹角以及两平面法向量的夹角求线线角、线面角及二面角．‎ ‎3. 会用向量的平行或垂直关系来推证空间线面的平行和垂直关系.‎ ‎1. 阅读：选修21第99～114页. ‎ ‎2. 解悟：①如何刻画直线、平面的方向；②如何求平面的法向量；③如何用空间向量的方法求线线角，线面角以及二面角的大小；④重解第104页例4，例5，第110页例4，体会解题方法并注意解题规范. ‎ ‎3. 践习：在教材空白处，完成第 112页练习第10题，第113页习题第5、6、9题. ‎ ‎　基础诊断　‎ ‎1. 已知＝(2，3，1)，＝(4，5，3)，则平面ABC的单位法向量为______________．‎ ‎2. 在棱长为a的正方体ABCDA1B1C1D1中，向量与向量所成角的大小为________．‎ ‎3. 在正四棱锥SABCD中，点O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面PAC所成角的大小是________．‎ ‎4. 在正方体ABCDA1B1C1D1中，E为BB1的中点，则平面A1ED与平面ABCD所成锐二面角的余弦值为________．‎ ‎5. 已知E，F分别是正方体ABCDA1B1C1D1的棱BC和CD的中点，求：‎ ‎(1) 写出直线A1D的一个方向向量：________________________________________________________________________；‎ ‎(2) 写出平面B1CD1的一个法向量：________．‎ ‎　范例导航　‎ 考向 求线线角、线面角、二面角的大小 ‎　　例1　如图，在长方体ABCDA′B′C′D′中，DA＝DC＝2，DD′＝1，A′C′与B′D′相交于点O′，点P在线段BD上(点P与点B不重合)．‎ ‎(1) 若异面直线O′P与BC′所成角的余弦值为，求DP的长度； ‎ ‎(2) 若DP＝，求平面PA′C′与平面DC′B所成角的正弦值．‎ 如图，在四棱锥PABCD中，PA⊥底面ABCD，底面ABCD是边长为2的菱形，∠ABC＝60°，PA＝，M为PC的中点．‎ ‎(1) 求异面直线PB与MD所成角的大小；‎ ‎(2) 求平面PCD与平面PAD所成的二面角的正弦值．‎ 考向 已知二面角求参数的值以及会求一些简单的存在性问题 ‎　　例2　如图，已知四棱锥PABCD的底面是菱形，对角线AC，BD交于点O，OA＝4，OB＝3，OP＝4，OP⊥底面ABCD.设点M满足＝λ(λ>0)．‎ ‎(1) 当λ＝时，求直线PA与平面BDM所成角的余弦值； ‎ ‎(2) 若二面角MABC的大小为，求λ的值．‎ 如图，在矩形ABCD中，已知AB＝1，BC＝a(a>0)，PA⊥平面ABCD，且PA＝1.‎ ‎(1) 试建立适当的坐标系，并写出点P，B，D的坐标；‎ ‎(2) 问当实数a在什么取值范围时，边BC上存在点Q，使得PQ⊥QD?‎ ‎(3) 当边BC上有且仅有一个点Q使得PQ⊥QD时，求二面角QPDA的余弦值．‎ ‎　自测反馈　‎ ‎1. 已知向量a＝(0，2，1)，b＝(－1，1，－2)，则a与b的夹角的大小为________．‎ ‎2. 如图，在直三棱柱ABCA1B1C1中，AB＝AC＝1，AA1＝2，∠B1A1C1＝90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为________．‎ ‎(第2题)‎ ‎　　　　(第4题)‎ ‎3. 在Rt△ABC中，∠C＝90°，AC＝BC＝1，PA⊥平面ABC，PA＝，则BP与平面PAC所成角的正切值为________．‎ ‎4. 如图，在直三棱柱ABCA1B1C1中，∠ACB＝90°，2AC＝AA1＝BC＝2.若二面角B1DCC1的大小为60°，则AD的长为________．‎ ‎1. 法向量不唯一，所以为了方便计算可以对x，y，z进行赋值．‎ ‎2. 求线线角需要注意角的范围，求二面角可以结合法向量的方向来判断是法向量的夹角还是补角．‎ ‎3. 你还有哪些体悟，写下来：‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ 第4课　空间向量的共线与共面 ‎　基础诊断　‎ ‎1. 或　解析：设平面ABC的法向量为n＝(x，y，1)，则n⊥且n⊥，即n·＝0且n·＝0，即即所以单位法向量为n2＝±＝±.‎ ‎2. 120°　解析：建立以点D为坐标原点，分别以，，为x轴，y轴，z轴建立空间直角坐标系，则B(a，a，0)，A1(a，0，a)，A(a，0，0)，C(0，a，0)．设与所成角为θ，则可得cosθ＝＝＝－，则θ＝120°.‎ ‎3. 30°　解析：以O为原点，OA为x轴，OB为y轴，OS为z轴建立空间直角坐标系．设OD＝SO＝OA＝OB＝OC＝a，则A(a，0，0)，B(0，a，0)，C(－a，0，0)，P，所以＝(2a，0，0)，＝.设平面PAC的法向量为n，可求得一个法向量为n＝(0，1，1)，则cos〈，n〉＝＝－，则cos〈，n〉＝120°，所以直线BC与平面PAC所成角的大小为120°－90°＝30°.‎ ‎4. 　解析：以A为原点，AB为x轴，AD为y轴，AA1为z轴建立空间直角坐标系，设该正方形棱长为1，则A1(0，0，1)，E，D(0，1，0)，所以＝(0，1，－1)，＝.设平面A1ED的法向量为m＝(1，y，z)，可得解得所以m＝(1，2，2)．因为平面ABCD的法向量为n＝(0，0，1)，所以cos〈m，n〉＝＝，即所成的锐二面角的余弦值为.‎ ‎5. (1) 　解析：因为多面体ABCDA1B1C1D1为正方体，根据正方体性质，所以A1D∥B1C，即为直线A1D的一个方向向量．(不唯一)‎ ‎(2) 　解析：连结DC1.因为AA1⊥平面A1B1C1D1，B1D1平面A1B1C1D1，所以AA1⊥B1D1.又因为四边形A1B1C1D1为正方形，所以B1D1⊥A1C1.又因为AA1∩A1C1＝A1，AA1，A1C1平面A1AC1，所以B1D1⊥平面A1AC1.又因为AC1平面A1AC1，所以 AC1⊥B1D1.同理可得AC1⊥CD1.因为CD1∩B1D1＝D1，CD1，B1D1平面B1CD1，所以AC1⊥平面B1CD1，即为平面B1CD1的法向量．(不唯一)．‎ ‎　范例导航　‎ 例1　解析：(1) 以D为坐标原点，DA为x轴，DC为y轴，DD′为z轴建立空间直角坐标系Dxyz.‎ 由题意，知D(0，0，0)，A′(2，0，1)，B(2，2，0)，C′(0，2，1)，O′(1，1，1)．‎ 设P(t，t，0)，‎ 所以＝(t－1，t－1，－1)，＝(－2，0，1)．‎ 设异面直线O′P与BC′所成角为θ，则|cosθ|＝＝＝，‎ 化简得21t2－20t＋4＝0，解得t＝或t＝，‎ 所以DP＝或DP＝.‎ ‎(2) 因为DP＝，所以P，‎ 则＝(0，2，1)，＝(2，2，0)，＝，＝，‎ 设平面DC′B的法向量为n1＝(x1，y1，z1)，‎ 所以即 所以取y1＝－1，则n1＝(1，－1，2)．‎ 设平面PA′C′的法向量n2＝(x2，y2，z2)，‎ 所以 即所以 取y2＝1，则n2＝(1，1，1)．‎ 设平面PA′C′与平面DC′B所成角为φ，‎ 所以|cosφ|＝＝＝，‎ 则sinφ＝.‎ 解析：(1) 设AC与BD交于点O，以点O为原点，分别以向量，，为x轴，y轴，z轴建立空间直角坐标系，‎ 则A(－1，0，0)，C(1，0，0)，B(0，－，0)，D(0，，0)，P(－1，0，)，M，‎ 所以＝，＝(1，－，－)，‎ 所以cos〈，〉＝＝＝0，‎ 则异面直线PB与MD所成的角为90°.‎ ‎(2) 设平面PCD的法向量为n1＝(x1，y1，z1)，平面PAD的法向量为n2＝(x2，y2，z2)．‎ 因为＝(－1，，0)，＝(1，，－)，‎ ＝(0，0，－)，‎ 由 令y1＝1，得平面PCD的一个法向量n1＝(，1，)，‎ 由 令y2＝－1，得平面PAD的一个法向量n2＝(，－1，0)，‎ 所以cos〈n1，n2〉＝＝＝，‎ 所以sin〈n1，n2〉＝.‎ 例2　解析：(1) 以O为坐标原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系Oxyz，则A(4，0，0)，B(0，3，0)，C(－4，0，0)，D(0，－3，0)，P(0，0，4)，所以＝(4，0，－4)，＝(0，6，0)，＝(－4，3，0)．‎ 当λ＝时，M，‎ 所以＝.‎ 设平面BDM的法向量为n＝(x，y，z)，‎ 则 令x＝2，则y＝0，z＝1，‎ 所以平面BDM的一个法向量为n＝(2，0，1)，‎ 所以cos〈，n〉＝＝，‎ 即直线PA与平面BDM所成角的余弦值为.‎ ‎(2) 由题可知平面ABC的一个法向量n1＝(0，0，1)．‎ 设M(a，0，b)，代入＝λ，得(a，0，b－4)＝λ(－4－a，0，－b)，‎ 解得即M，‎ 所以＝.‎ 设平面MAB的法向量为n2＝(x，y，z)，‎ 则 消去y，得(2λ＋1)x＝z，令x＝1，则z＝2λ＋1，y＝，‎ 所以平面MAB的一个法向量为n2＝(1，，2λ＋1)，‎ 所以＝，解得λ＝或－.‎ 因为λ>0，所以λ＝.‎ 解析：(1) 以A为坐标原点，AB，AD，AP分别为x轴，y轴，z轴建立空间直角坐标系如图所示．‎ 因为PA＝AB＝1，BC＝a，‎ 所以P(0，0，1)，B(1，0，0)，D(0，a，0)．‎ ‎(2) 设点Q(1，x，0)，‎ 则＝(1，x－a，0)，＝(－1，－x，1)．‎ 由·＝0，得x2－ax＋1＝0.‎ 当该方程有实数解时，边BC上才存在点Q，使得PQ⊥QD，故Δ＝a2－4≥0.‎ 因为a>0，故实数a的取值范围为a≥2.‎ ‎(3) 由(2)可知，当a＝2时，BC上仅有一点满足题意，此时x＝1，即Q为BC的中点．取AD的中点M，过点M作MN⊥PD，垂足为点N，连结QM，QN，则M(0，1，0)，P(0，0，1)，D(0，2，0)．‎ 因为D，N，P三点共线，‎ 所以＝＝＝＝.‎ 又＝(0，2，－1)，且·＝0，‎ 故·(0，2，－1)＝＝0，‎ 解得λ＝，‎ 所以＝，‎ 所以＝＋＝－＋＝(1，－，－)．‎ 因为·＝0＋2×＋(－1)×＝0，所以⊥，‎ 则∠MNQ为所求二面角的平面角，‎ 因为cos∠MNQ＝＝.‎ ‎　自测反馈　‎ ‎1. 90°　解析：cos〈a，b〉＝＝＝0，则a与b的夹角为90°.‎ ‎2. 　解析：以A为原点，分别以AB，AC，AA1所在直线为x轴，y轴，z轴建立空间直角坐标系，如图，A1(0，0，2)，C(0，1，0)，D(1，0，1)，C1(0，1，2)，‎ 则＝(1，－1，－1)，＝(0，1，－2)，所以||＝，||＝，·＝1，所以cos〈，〉＝＝，故异面直线C1D与A1C所成角的余弦值为.‎ ‎3. 　解析：由题意可得BC⊥平面PAC，则∠BPC为直线BP与平面PAC所成角，在Rt△BPC中，BC＝1，PC＝＝2，所以tan∠BPC＝＝.‎ ‎4. 　解析：以C为坐标原点，分别以CA，CB，CC1所在直线为x轴，y轴，z轴建立空间直角坐标系，则C(0，0，0)，A(1，0，0)，B1(0，2，2)，C1(0，0，2)．设AD＝a，则D(1，0，a)，＝(1，0，a)，＝(0，2，2)．设平面B1CD的法向量为m＝(x，y，z)，则可得令z＝－1，得m＝(a，1，－1)．又平面C1DC的一个法向量为n＝(0，1，0)，则由cos60°＝得＝，解得a＝，故AD＝.‎