【数学】2020届数学(理)一轮复习人教A版第23讲正弦定理和余弦定理学案
第23讲 正弦定理和余弦定理
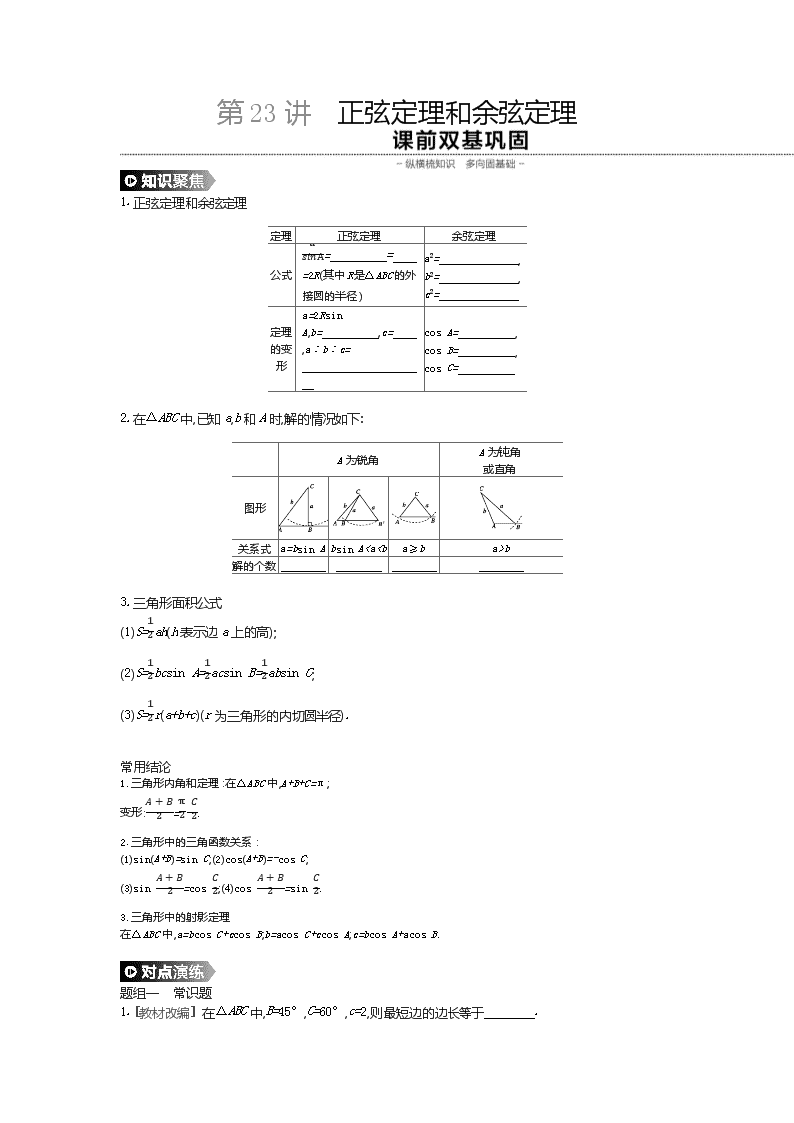
1.正弦定理和余弦定理
定理
正弦定理
余弦定理
公式
asinA= = =2R(其中R是△ABC的外接圆的半径)
a2= ,
b2= ,
c2=
定理
的变
形
a=2Rsin A,b= ,c= ,a∶b∶c=
cos A= ,
cos B= ,
cos C=
2.在△ABC中,已知a,b和A时,解的情况如下:
A为锐角
A为钝角
或直角
图形
关系式
a=bsin A
bsin A
b
解的个数
3.三角形面积公式
(1)S=12ah(h表示边a上的高);
(2)S=12bcsin A=12acsin B=12absin C;
(3)S=12r(a+b+c)(r为三角形的内切圆半径).
常用结论
1.三角形内角和定理:在△ABC中,A+B+C=π;
变形:A+B2=π2-C2.
2.三角形中的三角函数关系:
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
(3)sin A+B2=cos C2;(4)cos A+B2=sin C2.
3.三角形中的射影定理
在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
题组一 常识题
1.[教材改编] 在△ABC中,B=45°,C=60°,c=2,则最短边的边长等于 .
2.[教材改编] 在△ABC中,已知a=5,b=23,C=30°,则c= .
3.[教材改编] 在△ABC中,已知a2-c2+b2=ab,则C等于 .
4.[教材改编] 在△ABC中,已知a=32,b=23,cos C=13,则△ABC的面积为 .
题组二 常错题
◆索引:在△ABC中角与角的正弦的关系弄错;利用正弦定理求角时解的个数弄错;余弦定理、面积公式中边与角的三角函数的对应
关系弄错;三角形中的三角函数关系弄错.
5.在△ABC中,若sin A=sin B,则A,B的关系为 ;若sin A>sin B,则A,B的关系为 .
6.在△ABC中,若A=60°,a=43,b=42,则B等于 .
7.在△ABC中,a=2,b=3,C=60°,则c= ,△ABC的面积等于 .
8.在△ABC中,a,b,c分别为内角A,B,C所对的边,若ccos A=b,则△ABC为 三角形.
探究点一 利用正弦、余弦定理解三角形
例1 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a=3,且b2+c2=3+bc.
(1)求角A的大小;
(2)求bsin C的最大值.
[总结反思] (1)正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程,通过解方程求得未知元素;(2)正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,也可以把已知条件化为三角形边的关系;(3)涉及最值问题时,常利用基本不等式或表示为三角形的某一内角的三角函数形式求解.
变式题 (1)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a=23,c=22,1+tanAtanB=2cb,则C= ( )
A.π6 B.π4
C.π4或3π4 D.π3
(2)[2018·衡水中学月考] 已知△ABC满足BC·AC=22,若C=3π4,sinAsinB=12cos(A+B),则AB= .
探究点二 利用正弦、余弦定理判定三角形的形状
例2 已知在△ABC中,内角A,B,C所对的边分别为a,b,c,且b2+c2=a2+bc.若sin B·sin C=sin2A,则△ABC的形状是 ( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
[总结反思] 判断三角形的形状主要从两个角度考虑:(1)化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
变式题 在△ABC中,a,b,c分别为内角A,B,C所对的边,若tanAtanB=a2b2,则△ABC是 ( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形或等腰三角形
探究点三 与三角形面积有关的问题
例3 [2018·洛阳三模] 在△ABC中,内角A,B,C的对边分别为a,b,c且bsin B+(c-b)sin C=asin A.
(1)求角A的大小;
(2)若sin Bsin C=38,且△ABC的面积为23,求a.
[总结反思] (1)若已知一个角(角的大小或该角的正弦值、余弦值),一般结合题意求夹这个角的两边或两边之积,再代入公式求解;(2)若已知三边,可先求一个角的余弦值,再求正弦值,最后代入公式得面积;(3)若求面积的最值,一般表示为一个内角的三角函数,利用三角函数的性质求解,也可结合基本不等式求解.
变式题 [2018·黄冈中学月考] 在△ABC中,内角A,B,C的对边分别为a,b,c,且满足bc=1,a2-bc=(b-c)2.
(1)求△ABC的面积;
(2)若cos Bcos C=14,求△ABC的周长.
第23讲 正弦定理和余弦定理
考试说明 1.通过对任意三角形边长和角度的探索,掌握正弦定理、余弦定理.
2.能利用正弦定理和余弦定理解决一些简单的三角形度量问题.
【课前双基巩固】
知识聚焦
1.bsinB csinC b2+c2-2bccos A c2+a2-2accos B a2+b2-2abcos C 2Rsin B 2Rsin C sin A∶sin B∶sin C b2+c2-a22bc a2+c2-b22ca a2+b2-c22ab
2.一解 两解 一解 一解
对点演练
1.263 [解析] 易知A=75°,角B最小,所以边b最短.由正弦定理bsinB=csinC,得bsin45°=2sin60°,解得b=263.
2.7 [解析] 由余弦定理得c2=a2+b2-2abcos C=52+(23)2-2×5×23cos 30°=7,所以c=7.
3.60° [解析] 因为cos C=a2+b2-c22ab=12,所以C=60°.
4.43 [解析] 因为sin C=1-cos2C=223,所以△ABC的面积S=12absin C=43.
5.A=B A>B [解析] 根据正弦定理知,在△ABC中有sin A=sin B⇔a=b⇔A=B,sin A>sin B⇔a>b⇔A>B.
6.45° [解析] 由正弦定理知asinA=bsinB,则sin B=bsinAa=42×3243=22.又a>b,所以A>B,所以B为锐角,故B=45°.
7.7 332 [解析] 易知c=4+9-2×2×3×12=7,△ABC的面积等于12×2×3×32=332.
8.直角 [解析] ∵ccos A=b,∴由正弦定理得sin Ccos A=sin B=sin(A+C)=sin Acos C+cos Asin C,
整理得sin Acos C=0,
∵sin A≠0,
∴cos C=0,即C=90°,则△ABC为直角三角形.
【课堂考点探究】
例1 [思路点拨] (1)由余弦定理可得出;(2)用正弦定理将bsin C表示为关于C的三角函数,再结合C的取值范围求最大值.
解:(1)由a=3,b2+c2=3+bc,得b2+c2-a22bc=3+bc-a22bc=12,
即cos A=12,又∵A∈(0,π),∴A=π3.
(2)由正弦定理,得b=asinAsin B=2sin B,
∴bsin C=2sin Csin B=2sin Csin2π3-C=2sin C12sinC+32cosC=sin2C+3sin Ccos C=32sin 2C-12cos 2C+12=sin2C-π6+12.∵0
查看更多