(新人教版选修3-2)物理:第四节:法拉第电磁感应定律同步练习二
法拉第电磁感应定律同步练习二
一.基础达标:
1、法拉第电磁感应定律可以这样表述:闭合电路中感应电动势的大小 ( )
A.跟穿过这一闭合电路的磁通量成正比
B.跟穿过这一闭合电路的磁感应强度成正比
C.跟穿过这一闭合电路的磁通量的变化率成正比
D.跟穿过这一闭合电路的磁通量的变化量成正比
2、将一磁铁缓慢地或迅速地插到闭合线圈中同样位置处,不发生变化的物理量有 ( )
21 世纪教育网
A.磁通量的变化率
B.感应电流的大小
C.消耗的机械功率
D.磁通量的变化量
E.流过导体横截面的电荷量
3、恒定的匀强磁场中有一圆形闭合导线圈,线圈平面垂直于磁场方向,当线圈在磁场中做
下列哪种运动时,线圈中能产生感应电流 ( )
A.线圈沿自身所在平面运动
B.沿磁场方向运动
C.线圈绕任意一直径做匀速转动
D.线圈绕任意一直径做变速转动
4、一个矩形线圈,在匀强磁场中绕一个固定轴做匀速运动,当线圈处于如图所示位置时,
此线圈 ( )
A.磁通量最大,磁通量变化率最大,感应电动势最小
B.磁通量最大,磁通量变化率最大,感应电动势最大
C.磁通量最小,磁通量变化率最大,感应电动势最大
D.磁通量最小,磁通量变化率最小,感应电动势最小
5、一个 N 匝的圆线圈,放在磁感应强度为 B 的匀强磁场中,线圈平面跟磁感应强度方向成
30°角,磁感应强度随时间均匀变化,线圈导线规格不变.下列方法中可使线圈中感应
电流增加一倍的是 ( )
A.将线圈匝数增加一倍
B.将线圈面积增加一倍
C.将线圈半径增加一倍
D.适当改变线圈的取向
6、闭合电路中产生的感应电动势的大小,跟穿过这一闭合电路的下列哪个物理量成正比
( )
A、磁通量
B、磁感应强度
C、磁通量的变化率
D、磁通量的变化量
7、穿过一个单匝数线圈的磁通量,始终为每秒钟均匀地增加 2 Wb,则( )
A、线圈中的感应电动势每秒钟增大 2 V
B、线圈中的感应电动势每秒钟减小 2 V
C、线圈中的感应电动势始终为 2 V
D、线圈中不产生感应电动势
8、如图 1 所示,矩形金属框置于匀强磁场中,ef 为一导体棒,可在 ab 和 cd 间滑动并接触
良好;设磁感应强度为 B,ef 长为 L,在Δt 时间内向左匀速滑过距离Δd,由电磁感应
定律 E=n
t
可知,下列说法正确的是( )
图 1
A、当 ef 向左滑动时,左侧面积减少 L·Δd,右侧面积增加 L·Δd,因此 E=2BLΔd/Δt
B、当 ef 向左滑动时,左侧面积减小 L·Δd,右侧面积增大 L·Δd,互相抵消,因此 E=0
C、在公式 E=n
t
中,在切割情况下,ΔΦ=B·ΔS,ΔS 应是导线切割扫过的面积,
因此 E=BLΔd/Δt
D、在切割的情况下,只能用 E=BLv 计算,不能用 E=n
t
计算
9、在南极上空离地面较近处,有一根与地面平行的直导线,现让直导线由静止自由下落,
在下落过程中,产生的感应电动势( )
A、增大
B、减小
C、不变
D、无法判断
10、一个 200 匝、面积为 20 cm2 的线圈,放在磁场中,磁场的方向与线圈平面成 30°角,
若磁感应强度在 0.05 s 内由 0.1 T 增加到 0.5 T.在此过程中穿过线圈的磁通量的变化是
___________ Wb;磁通量的平均变化率是___________ Wb/s;线圈中的感应电动势的大
小是___________ V.
二.能力提升:
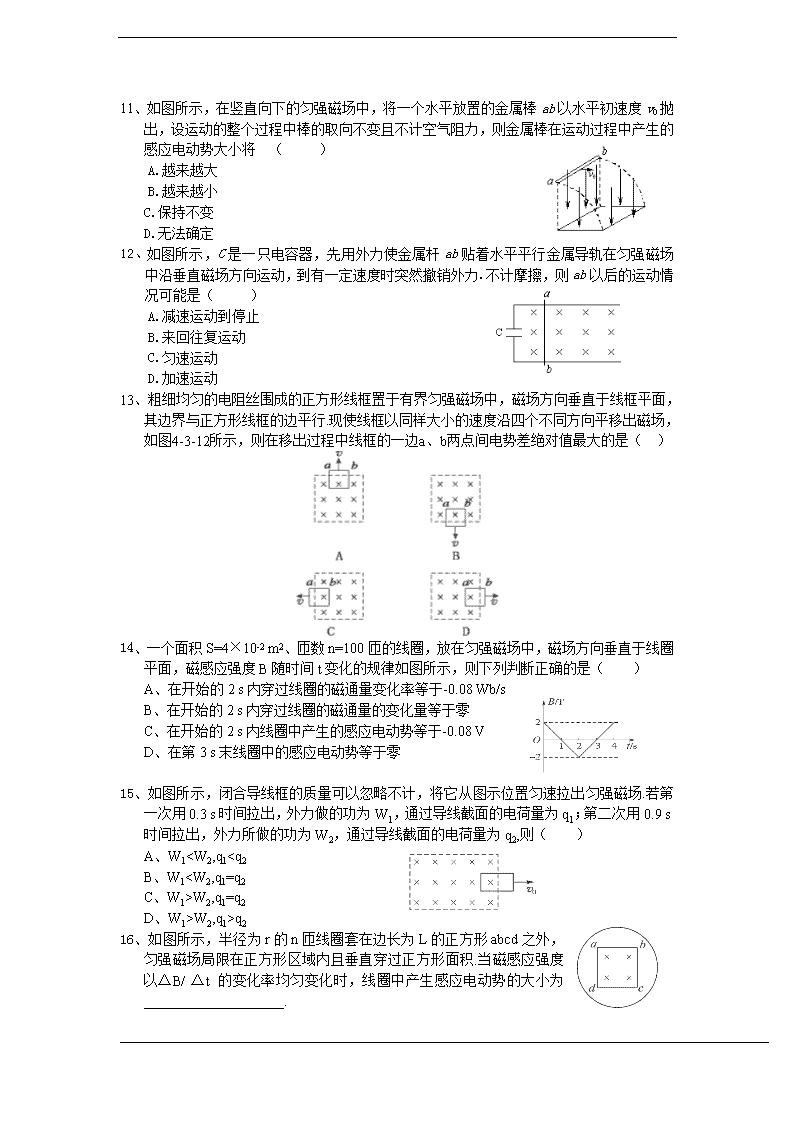
11、如图所示,在竖直向下的匀强磁场中,将一个水平放置的金属棒 ab 以水平初速度 v0 抛
出,设运动的整个过程中棒的取向不变且不计空气阻力,则金属棒在运动过程中产生的
感应电动势大小将 ( )
A.越来越大
B.越来越小
C.保持不变
D.无法确定
12、如图所示,C 是一只电容器,先用外力使金属杆 ab 贴着水平平行金属导轨在匀强磁场
中沿垂直磁场方向运动,到有一定速度时突然撤销外力.不计摩擦,则 ab 以后的运动情
况可能是( )
A.减速运动到停止
B.来回往复运动
C.匀速运动
D.加速运动
13、粗细均匀的电阻丝围成的正方形线框置于有界匀强磁场中,磁场方向垂直于线框平面,
其边界与正方形线框的边平行.现使线框以同样大小的速度沿四个不同方向平移出磁场,
如图4-3-12所示,则在移出过程中线框的一边a、b两点间电势差绝对值最大的是( )
14、一个面积 S=4×10-2 m2、匝数 n=100 匝的线圈,放在匀强磁场中,磁场方向垂直于线圈
平面,磁感应强度 B 随时间 t 变化的规律如图所示,则下列判断正确的是( )
A、在开始的 2 s 内穿过线圈的磁通量变化率等于-0.08 Wb/s
B、在开始的 2 s 内穿过线圈的磁通量的变化量等于零
C、在开始的 2 s 内线圈中产生的感应电动势等于-0.08 V
D、在第 3 s 末线圈中的感应电动势等于零
15、如图所示,闭合导线框的质量可以忽略不计,将它从图示位置匀速拉出匀强磁场.若第
一次用 0.3 s 时间拉出,外力做的功为 W1,通过导线截面的电荷量为 q1;第二次用 0.9 s
时间拉出,外力所做的功为 W2,通过导线截面的电荷量为 q2,则( )
A、W1
W2,q1=q2
D、W1>W2,q1>q2
16、如图所示,半径为 r 的 n 匝线圈套在边长为 L 的正方形 abcd 之外,
匀强磁场局限在正方形区域内且垂直穿过正方形面积.当磁感应强度
以 Δ B/ Δ t 的 变 化 率 均 匀 变 化 时 , 线 圈 中 产 生 感 应 电 动 势 的 大 小 为
____________________.
17、在图中,EF、GH 为平行的金属导轨,其电阻可不计,R 为电阻器,C 为电容器,AB
为可在 EF 和 GH 上滑动的导体横杆.有均匀磁场垂直于导轨平面.若用 I1 和 I2 分别表示图
中该处导线中的电流,则当横杆 AB( )
A、匀速滑动时,I1=0,I2=0
B、匀速滑动时,I1≠0,I2≠0
C、加速滑动时,I1=0,I2=0
D、加速滑动时,I1≠0,I2≠0
18、如图 4-3-10 所示,在光滑的绝缘水平面上,一个半径为 10 cm、
电阻为 1.0 Ω、质量为 0.1 kg 的金属环以 10 m/s 的速度冲入一有
界磁场,磁感应强度为 B=0.5 T.经过一段时间后,圆环恰好有一半
进入磁场,该过程产生了 3.2 J 的电热,则此时圆环的瞬时速度为
___________m/s;瞬时加速度为___________ m/s2.
19、如图所示,接有灯泡 L 的平行金属导轨水平放置在匀强磁场中,
一导体杆与两导轨良好接触并做往复运动,其运动情况与弹簧振子做简谐运动的情况相
同.图中 O 位置对应于弹簧振子的平衡位置,P、Q 两位置对应于弹簧振子的最大位移处.
若两导轨的电阻不计,则( )
A、杆由 O 到 P 的过程中,电路中电流变大
B、杆由 P 到 Q 的过程中,电路中电流一直变大
C、杆通过 O 处时,电路中电流方向将发生改变
D、杆通过O处时,电路中电流最大
20、如图 4-3-14 所示,半径为 R 的圆形导轨处在垂直于圆平面的匀强磁场中,磁感应强度
为 B,方向垂直于纸面向内.一根长度略大于导轨直径的导体棒 MN 以速率 v 在圆导轨上
从左端滑到右端,电路中的定值电阻为 r,其余电阻不计.导体棒与圆形导轨接触良好.
求:
(1)、在滑动过程中通过电阻 r 的电流的平均值;
(2)、MN 从左端到右端的整个过程中,通过 r 的电荷量;
(3)、当 MN 通过圆导轨中心时,通过 r 的电流是多大?
21、如图所示,两根平行且足够长的金属导轨置于磁感应强度为 B 的匀强磁场中,磁场的
方向垂直于导轨平面,两导轨间距为 L,左端连一电阻 R,右端连一电容器 C,其余电
阻不计。长为 2L 的导体棒 ab 与从图中实线位置开始,以 a 为圆心沿顺时针方向的角速
度ω匀速转动,转 90°的过程中,通过电阻 R 的电荷量为多少?
[来源:21世纪教育网]
22.如图所示,水平放置的导体框架,宽 L=0.50 m,接有电阻 R=0.20 Ω,匀强磁场垂直框
架平面向里,磁感应强度 B=0.40 T.一导体棒 ab 垂直框边跨放在框架上,并能无摩擦地
在框架上滑动,框架和导体 ab 的电阻均不计.当 ab 以 v=4.0 m/s 的速度向右匀速滑动时,
求:
(1)ab 棒中产生的感应电动势大小;
(2)维持导体棒 ab 做匀速运动的外力 F 的大小;
(3)若将外力 F 突然减小到 F′,简要论述导体 ab 以后的运动情况.
23、如图 4-3-18 所示,在磁感应强度为 B 的匀强磁场中有一个面积为 S 的矩形线圈绕垂直
于磁感线的对称轴 OO′以角速度ω匀速转动.
(1)穿过线框平面磁通量的变化率何时最大?最大值为多少?
(2)当线框由图示位置转过 60°的过程中,平均感应电动势为多大?
(3)线框由图示位置转到 60°时瞬时感应电动势为多大?
24、横截面积 S=0.2 m2、n=100 匝的圆形线圈 A 处在如图所示的磁场内,磁感应强度变化率
为 0.02 T/s.开始时 S 未闭合,R1=4 Ω,R2=6Ω,C=30 μF,线圈内阻不计,求:
(1)闭合 S 后,通过 R2 的电流的大小;
(2)闭合 S 后一段时间又断开,问 S 断开后通过 R2 的电荷量是多少?
[来源:21 世纪教育网]
参考答案:
1、C
2、DE
3、CD
4、C
5、CD
6、C
7、C
8、C
9、C 21 世纪教育网
10、磁通量的变化量是由磁场的变化引起的,所以
ΔΦ=ΔBSsinθ=(0.5-0.1)×20×10-4×0.5 Wb=4×10-4 Wb
磁通量的变化率
t
=
05.0
104 4 Wb/s=8×10-3 Wb/s21 世纪教育网
感应电动势 E=n
t
=200×8×10-3 V=1.6 V.
答案:4×10-4 8×10-3 1.6
11、C
12、C
13、B
14、A
15、C
16、n
t
B
L2
17、D
18、根据能量守恒定律,动能的减少等于产生的电热,即
2
1 mv2-
2
1 mv12=E热,代入数据解
得:v1=6 m/s.此时切割磁感线的有效长度为圆环直径,故瞬时电动势为E=Blv1,瞬时电
流I=
R
E ,安培力F=BIl,瞬时加速度为a=
m
F ,整理得:a=
Rm
vlB 1
22
=0.6 m/s2.
19、D
20、思路解析:导体棒从左向右滑动的过程中,切割磁感线产生感应电动势,对电阻 r 供电.
(1)、计算平均电流,应该用法拉第电磁感应定律,先求出平均感应电动势.整个过程磁
通量的变化为ΔΦ=BS=BπR2,所用的时间Δt=
v
R2 ,代入公式 E=
t
=
2
BRv ,平均
电流为 I=
r
BRv
r
E
2
.
(2)、电荷量的运算应该用平均电流,q=IΔt=
r
RB 2 .
(3)、当 MN 通过圆形导轨中心时,切割磁感线的有效长度最大,l=2R,根据导体切割磁
感线产生的电动势公式 E=Blv 得:E=B·2Rv,此时通过 r 的电流为 I=
r
BRv
r
E 2 .
答案:(1)
r
BRv
2
(2)
r
RB 2 (3)
r
BRv2
21、思路解析:以 a 为圆心转动 90°的过程可分为两个阶段,第一阶段是导体棒与导轨接
触的过程;第二阶段是导体棒转动 60°以后 b 端离开导轨以后.
第一阶段导体棒切割磁感线产生感应电动势,因为切割磁感线的有效长度发生变化,所
以电动势是改变的,该过程中通过电阻 R 的电荷量可用平均电动势来求出.该过程中相
当于电源的导体棒给电容器 C 充电.
平均电动势 E1=
t
,ΔΦ=BΔS=
2
3 BL2,通过 R 的电荷量 q1=
R
E1 Δt=
R
BL
2
3 2
.
第二阶段,电容器要对电阻放电,电容器的电荷量完全通过电阻放完.电容器充电的最大
电压为 E2=
2
1 B(2L)2ω,此时电容器的充电电荷量为 q2=CE2=2BL2Cω.
整个过程通过电阻的总的电荷量为 Q=q1+q2=
R
BL
2
3 2
+2BL2Cω.
答案:
R
BL
2
3 2
+2BL2Cω
22、 (1)E=0.80 V (2)F=0.80 N (3)略
23、 (1)ab 与 cd 两边垂直切割磁感线时,Em=BSω
(2) E = 2
3 BSω
(3)
2
3 BSω
24、解:(1)磁感应强度变化率的大小为
t
B
=0.02 T/s,B 逐渐减弱,
所以 E=n
t
BS
=100×0. 02×0.2 V=0.4 V
I=
64
4.0
21 RR
E A=0.04 A,方向从上向下流过 R2.
(2)R2 两端的电压为 U2=
64
6
21
2
ERR
R ×0.4 V=0.24 V
所以 Q=CU2=30×10-6×0.04 C=7.2×10-6 C.