2018届二轮复习求轨迹方程的常用方法学案（全国通用）

2018届二轮复习求轨迹方程的常用方法学案（全国通用）

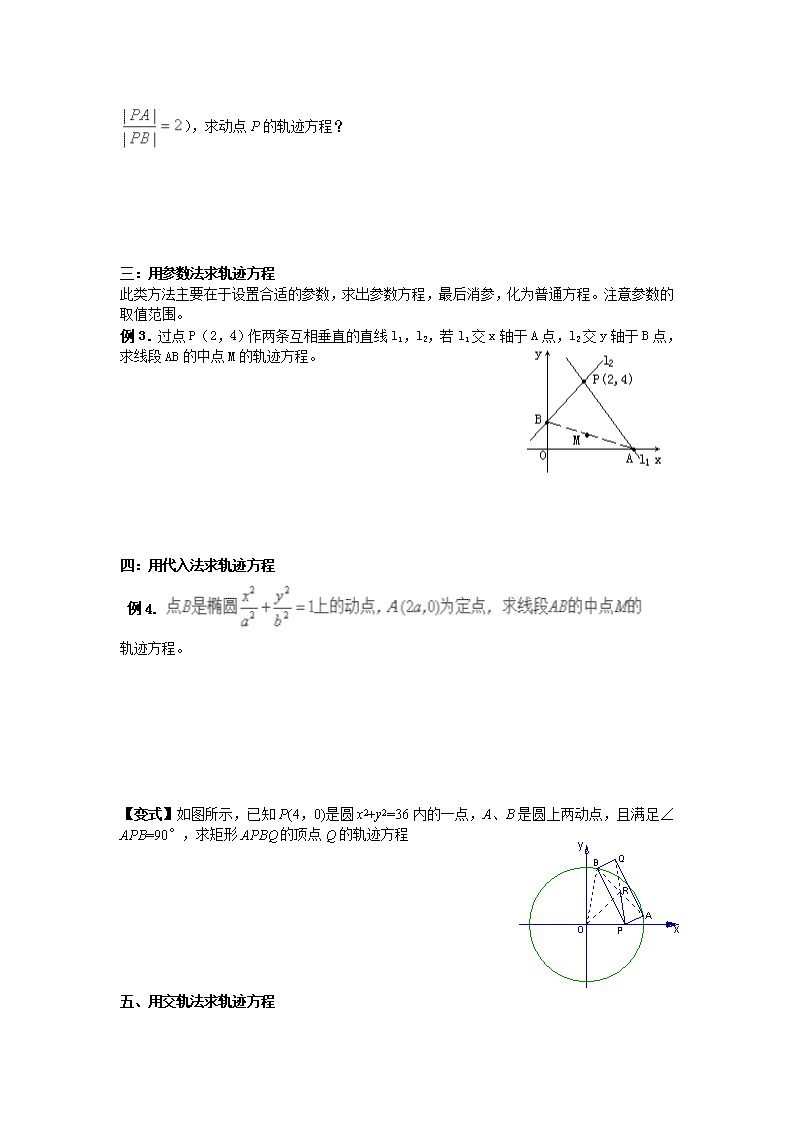
求轨迹方程的常用方法 ‎ ‎（一）求轨迹方程的一般方法：‎ ‎1. 定义法：如果动点P的运动规律合乎我们已知的某种曲线（如圆、椭圆、双曲线、抛物线）的定义，则可先设出轨迹方程，再根据已知条件，待定方程中的常数，即可得到轨迹方程。 ‎ ‎ 2. 直译法：如果动点P的运动规律是否合乎我们熟知的某些曲线的定义难以判断，但点P满足的等量关系易于建立，则可以先表示出点P所满足的几何上的等量关系，再用点P的坐标（x，y）表示该等量关系式，即可得到轨迹方程。‎ ‎ 3. 参数法：如果采用直译法求轨迹方程难以奏效，则可寻求引发动点P运动的某个几何量t，以此量作为参变数，分别建立P点坐标x，y与该参数t的函数关系x＝f（t），‎ y＝g（t），进而通过消参化为轨迹的普通方程F（x，y）＝0。‎ ‎ 4. 代入法（相关点法）：如果动点P的运动是由另外某一点P'的运动引发的，而该点的运动规律已知，（该点坐标满足某已知曲线方程），则可以设出P（x，y），用（x，y）表示出相关点P'的坐标，然后把P'的坐标代入已知曲线方程，即可得到动点P的轨迹方程。‎ ‎5：交轨法：在求动点轨迹时，有时会出现要求两动曲线交点的轨迹问题，这种问题通常通过解方程组得出交点（含参数）的坐标，再消去参数求得所求的轨迹方程（若能直接消去两方程的参数，也可直接消去参数得到轨迹方程），该法经常与参数法并用。‎ 一：用定义法求轨迹方程 例1：已知的顶点A，B的坐标分别为（-4，0），（4，0），C 为动点，且满足 求点C的轨迹。‎ ‎【变式】：已知圆的圆心为M1，圆的圆心为M2，一动圆与这两个圆外切，求动圆圆心P的轨迹方程。‎ 二：用直译法求轨迹方程 此类问题重在寻找数量关系。‎ 例2：一条线段两个端点A和B分别在x轴和y轴上滑动，且BM=a，AM=b，求AB中点M的轨迹方程？‎ ‎【变式】: 动点P（x,y）到两定点A（－3，0）和B（3，0）的距离的比等于2（即 ‎），求动点P的轨迹方程？‎ 三：用参数法求轨迹方程 此类方法主要在于设置合适的参数，求出参数方程，最后消参，化为普通方程。注意参数的取值范围。‎ 例3．过点P（2，4）作两条互相垂直的直线l1，l2，若l1交x轴于A点，l2交y轴于B点，求线段AB的中点M的轨迹方程。‎ ‎ ‎ 四：用代入法求轨迹方程 ‎ 例4. ‎ 轨迹方程。‎ ‎ ‎ ‎【变式】如图所示，已知P(4，0)是圆x2+y2=36内的一点，A、B是圆上两动点，且满足∠APB=90°，求矩形APBQ的顶点Q的轨迹方程 ‎ 五、用交轨法求轨迹方程 例5.已知椭圆（a＞b＞o）的两个顶点为,，与y轴平行的直线交椭圆于P1、P2，求A1P1与A2P2交点M的轨迹方程.‎ 六、用点差法求轨迹方程 例6. 已知椭圆，‎ ‎（1）求过点且被平分的弦所在直线的方程；‎ ‎（2）求斜率为2的平行弦的中点轨迹方程；‎ ‎（3）过引椭圆的割线，求截得的弦的中点的轨迹方程；‎ 练习 ‎1.在中，B，C 坐标分别为（-3，0），（3，0），且三角形周长为16，则点A的轨迹方 程是_______________________________.‎ ‎2.两条直线与的交点的轨迹方程是 __________ .‎ ‎3.已知圆的方程为(x-1)2+y2=1,过原点O作圆的弦‎0A，则弦的中点M的轨迹方程是 _____‎ ‎4.当参数m随意变化时，则抛物线的顶点的轨迹方程为______。‎ ‎5:点M到点F（4，0）的距离比它到直线的距离小1，则点M的轨迹方程为________。‎ ‎6:求与两定点距离的比为1：2的点的轨迹方程为_____________‎ ‎7.抛物线的通径（过焦点且垂直于对称轴的弦）与抛物线交于A、B两点，动点C在抛物线上，求△ABC重心P的轨迹方程。‎ ‎8.已知动点P到定点F（1，0）和直线x=3的距离之和等于4，求点P的轨迹方程。‎ ‎9.过原点作直线l和抛物线交于A、B两点，求线段AB的中点M的轨迹方程。‎ 参考答案 例1：已知的顶点A，B的坐标分别为（-4，0），（4，0），C 为动点，且满足求点C的轨迹。‎ ‎【解析】由可知，即，满足椭圆的定义。令椭圆方程为，则，则轨迹方程为 ‎（，图形为椭圆（不含左，右顶点）。‎ ‎【变式1】: 1:已知圆的圆心为M1，圆的圆心为M2，一动圆与这两个圆外切，求动圆圆心P的轨迹方程。‎ 解：设动圆的半径为R，由两圆外切的条件可得：，。‎ ‎。‎ ‎∴动圆圆心P的轨迹是以M1、M2为焦点的双曲线的右支，c=4，a=2，b2=12。‎ 故所求轨迹方程为 ‎2:一动圆与圆O：外切，而与圆C：内切，那么动圆的圆心M的轨迹是：‎ A：抛物线B：圆 C：椭圆 D：双曲线一支 ‎【解答】令动圆半径为R，则有，则|MO|-|MC|=2，满足双曲线定义。故选D。‎ 二：用直译法求曲线轨迹方程 此类问题重在寻找数量关系。‎ 例2： 一条线段AB的长等于‎2a,两个端点A和B分别在x轴和y轴上滑动，求AB中点P的轨迹方程？‎ 解 设M点的坐标为 由平几的中线定理：在直角三角形AOB中，OM=‎ M点的轨迹是以O为圆心，a为半径的圆周.‎ ‎【变式2】: 动点P（x,y）到两定点A（－3，0）和B（3，0）的距离的比等于2（即），求动点P的轨迹方程？‎ ‎【解答】∵|PA|=‎ 代入得 化简得（x－5）2+y2=16，轨迹是以（5，0）为圆心，4为半径的圆.‎ 三：用参数法求曲线轨迹方程 此类方法主要在于设置合适的参数，求出参数方程，最后消参，化为普通方程。注意参数的取值范围。‎ 例3．过点P（2，4）作两条互相垂直的直线l1，l2，若l1交x轴于A点，l2交y轴于B点，求线段AB的中点M的轨迹方程。‎ ‎【解析】‎ 分析1：从运动的角度观察发现，点M的运动是由直线l1引发的，可设出l1的斜率k作为参数，建立动点M坐标（x，y）满足的参数方程。‎ 解法1：设M（x，y），设直线l1的方程为y－4＝k（x－2），（k≠０）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∵M为AB的中点，‎ ‎ ‎ ‎ 消去k，得x＋2y－5＝0。‎ ‎ 另外，当k＝0时，AB中点为M（1，2），满足上述轨迹方程；‎ ‎ 当k不存在时，AB中点为M（1，2），也满足上述轨迹方程。‎ ‎ 综上所述，M的轨迹方程为x＋2y－5＝0。‎ ‎ 分析2：解法1中在利用k1k2＝－1时，需注意k1、k2是否存在，故而分情形讨论，能否避开讨论呢？只需利用△PAB为直角三角形的几何特性：‎ ‎ ‎ ‎ 解法2：设M（x，y），连结MP，则A（2x，0），B（0，2y），‎ ‎ ∵l1⊥l2，∴△PAB为直角三角形 ‎ ‎ ‎ ‎ 化简，得x＋2y－5＝0，此即M的轨迹方程。‎ 分析3：：设M（x，y），由已知l1⊥l2，联想到两直线垂直的充要条件：k1k2＝－1，即可列出轨迹方程，关键是如何用M点坐标表示A、B两点坐标。事实上，由M为AB的中点，易找出它们的坐标之间的联系。‎ 解法3：设M（x，y），∵M为AB中点，∴A（2x，0），B（0，2y）。‎ ‎ 又l1，l2过点P（2，4），且l1⊥l2‎ ‎ ∴PA⊥PB，从而kPA·kPB＝－1，‎ ‎ ‎ ‎ ‎ ‎ 注意到l1⊥x轴时，l2⊥y轴，此时A（2，0），B（0，4）‎ ‎ 中点M（1，2），经检验，它也满足方程x＋2y－5＝0‎ ‎ 综上可知，点M的轨迹方程为x＋2y－5＝0。‎ ‎【变式3】过圆O：x2 +y2= 4 外一点A（4，0），作圆的割线，求割线被圆截得的弦BC的中点M的轨迹。‎ ‎ ‎ 解法一：“几何法”‎ ‎ 设点M的坐标为（x,y）,因为点M 是弦BC的中点，所以OM⊥BC,‎ ‎ 所以|OM | ２＋|ＭＡ|２　＝|ＯＡ| ２　， 即(x2 +y2)+(x －４)2 +y2 =16‎ ‎ 化简得：（x－2）2+ y2 =4................................①‎ ‎ 由方程 ① 与方程x2 +y2= 4得两圆的交点的横坐标为1，所以点M的轨迹方程为 ‎ （x－2）2+ y2 =4 （0≤x＜1）。所以M的轨迹是以（2，0）为圆心，‎ ‎2为半径的圆在圆O内的部分。‎ 解法二：“参数法”‎ ‎ 设点M的坐标为（x,y），B（x1,y1）,C（x2,y2）直线AB的方程为y=k(x－4),‎ 由直线与圆的方程得（1+k2）x2 －8k2x +16k2－4=0...........(*),‎ 由点M为BC的中点，所以x=...............(1) , 又OM⊥BC，所以 k=.................(2)由方程（1）（2）‎ 消去k得（x－2）2+ y2 =4,又由方程（*）的△≥0得k2 ≤,所以x＜1.‎ 所以点M的轨迹方程为（x－2）2+ y2 =4 （0≤x＜1）所以M的轨迹是以（2，0）为圆心，‎ ‎2为半径的圆在圆O内的部分。‎ 四：用代入法等其它方法求轨迹方程 ‎ 例4. ‎ 轨迹方程。‎ ‎ 分析：题中涉及了三个点A、B、M，其中A为定点，而B、M为动点，且点B的运动是有规律的，显然M的运动是由B的运动而引发的，可见M、B为相关点，故采用相关点法求动点M的轨迹方程。‎ ‎ 【解析】设动点M的坐标为（x，y），而设B点坐标为（x0，y0）‎ ‎ 则由M为线段AB中点，可得 ‎ 即点B坐标可表为（2x－‎2a，2y）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎【变式4】如图所示，已知P(4，0)是圆x2+y2=36内的一点，A、B是圆上两动点，且满足∠APB=90°，求矩形APBQ的顶点Q的轨迹方程 ‎ ‎【解析】： 设AB的中点为R，坐标为(x,y)，则在Rt△ABP中，|AR|=|PR| 又因为R是弦AB的中点，依垂径定理 在Rt△OAR中，|AR|2=|AO|2－|OR|2=36－(x2+y2)‎ 又|AR|=|PR|=‎ 所以有(x－4)2+y2=36－(x2+y2),即x2+y2－4x－10=0‎ 因此点R在一个圆上，而当R在此圆上运动时，Q点即在所求的轨迹上运动 ‎ 设Q(x,y)，R(x1,y1)，因为R是PQ的中点，所以x1=,‎ 代入方程x2+y2－4x－10=0,得 ‎－10=0‎ 整理得 x2+y2=56,这就是所求的轨迹方程 ‎ 五、用交轨法求轨迹方程 六、用点差法求轨迹方程 ‎ ‎ 分析：此题中四问都跟弦中点有关，因此可考虑设弦端坐标的方法．‎ 解：设弦两端点分别为，，线段的中点，则 ‎①－②得．‎ 由题意知，则上式两端同除以，有，‎ 将③④代入得．⑤‎ ‎（1）将，代入⑤，得，故所求直线方程为： ． ⑥‎ 将⑥代入椭圆方程得，符合题意，为所求．‎ ‎（2）将代入⑤得所求轨迹方程为： ．（椭圆内部分）‎ ‎（3）将代入⑤得所求轨迹方程为： ．（椭圆内部分）‎ 练习1【正确解答】ABC为三角形，故A，B，C不能三点共线。轨迹方程里应除去点，即轨迹方程为 ‎2.两条直线与的交点的轨迹方程是 .‎ ‎【解答】:直接消去参数即得(交轨法):‎ ‎3:已知圆的方程为(x-1)2+y2=1,过原点O作圆的弦‎0A，则弦的中点M的轨迹方程是 .‎ ‎【解答】:令M点的坐标为(,则A的坐标为(2,代入圆的方程里面得:‎ ‎4:当参数m随意变化时，则抛物线的顶点的轨迹方程为 ‎【分析】：把所求轨迹上的动点坐标x，y分别用已有的参数m来表示，然后消去参数m，便可得到动点的轨迹方程。【解答】：抛物线方程可化为 它的顶点坐标为 消去参数m得：‎ 故所求动点的轨迹方程为。‎ ‎5:点M到点F（4，0）的距离比它到直线的距离小1，则点M的轨迹方程为 ‎【分析】：点M到点F（4，0）的距离比它到直线的距离小1，意味着点M到点F（4，0）的距离与它到直线的距离相等。由抛物线标准方程可写出点M的轨迹方程。‎ ‎【解答】：依题意，点M到点F（4，0）的距离与它到直线的距离相等。则点M的轨迹是以F（4，0）为焦点、为准线的抛物线。故所求轨迹方程为。‎ ‎6:求与两定点距离的比为1：2的点的轨迹方程为_________‎ ‎【分析】:设动点为P，由题意，则依照点P在运动中所遵循的条件，可列出等量关系式。‎ ‎【解答】：设是所求轨迹上一点，依题意得 由两点间距离公式得：‎ 化简得：‎ ‎7抛物线的通径（过焦点且垂直于对称轴的弦）与抛物线交于A、B两点，动点C在抛物线上，求△ABC重心P的轨迹方程。‎ ‎【分析】：抛物线的焦点为。设△ABC重心P的坐标为，点C的坐标为。其中 ‎【解答】：因点是重心，则由分点坐标公式得：‎ 即 由点在抛物线上，得：‎ 将代入并化简，得：（‎ ‎9.已知动点P到定点F（1，0）和直线x=3的距离之和等于4，求点P的轨迹方程。‎ ‎【解答】：设点P的坐标为（x，y），则由题意可得。‎ ‎（1）当x≤3时，方程变为，化简得。‎ ‎（2）当x>3时，方程变为，化简得。‎ 故所求的点P的轨迹方程是或 ‎10.过原点作直线l和抛物线交于A、B两点，求线段AB的中点M的轨迹方程。‎ ‎【解答】：由题意分析知直线l的斜率一定存在，设直线l的方程y=kx。把它代入抛物线方程，得。因为直线和抛物线相交，所以△>0，解得。‎ 设A（），B（），M（x，y），由韦达定理得。‎ 由消去k得。‎ 又，所以。‎ ‎∴点M的轨迹方程为。‎