2019届二轮复习选择填空标准练(12)作业(全国通用)
2019届二轮复习 选择填空标准练 (12) 作业(全国通用)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x∈N|x(3-x)≥0},B={x|-2≤x≤2},则A∩B= ( )
A.{x|0≤x≤2} B.{0,1,2}
C.{x|0
0时,f(x)=2x+2x-4,则f(x)的零点个数是 ( )
A.2 B.3 C.4 D.5
【解析】选B.由于函数是定义在R上的奇函数,故f(0)=0.由于f·f(2)<0,而函数在x>0时单调递增,故在x>0时有1个零点,根据奇函数的对称性可知,在x<0时,也有1个零点.故一共有3个零点.
7.函数f(x)=(其中e为自然对数的底数)的图象大致为 ( )
【解析】选D.由题意得函数的定义域为(-∞,0)∪(0,+∞).
因为f(-x)==-==f(x),
所以函数f(x)为偶函数,可排除选项A,C.
又f(x)===+,
所以f′(x)=--,
所以当x>0时,f′(x)<0,f(x)单调递减,可排除B.
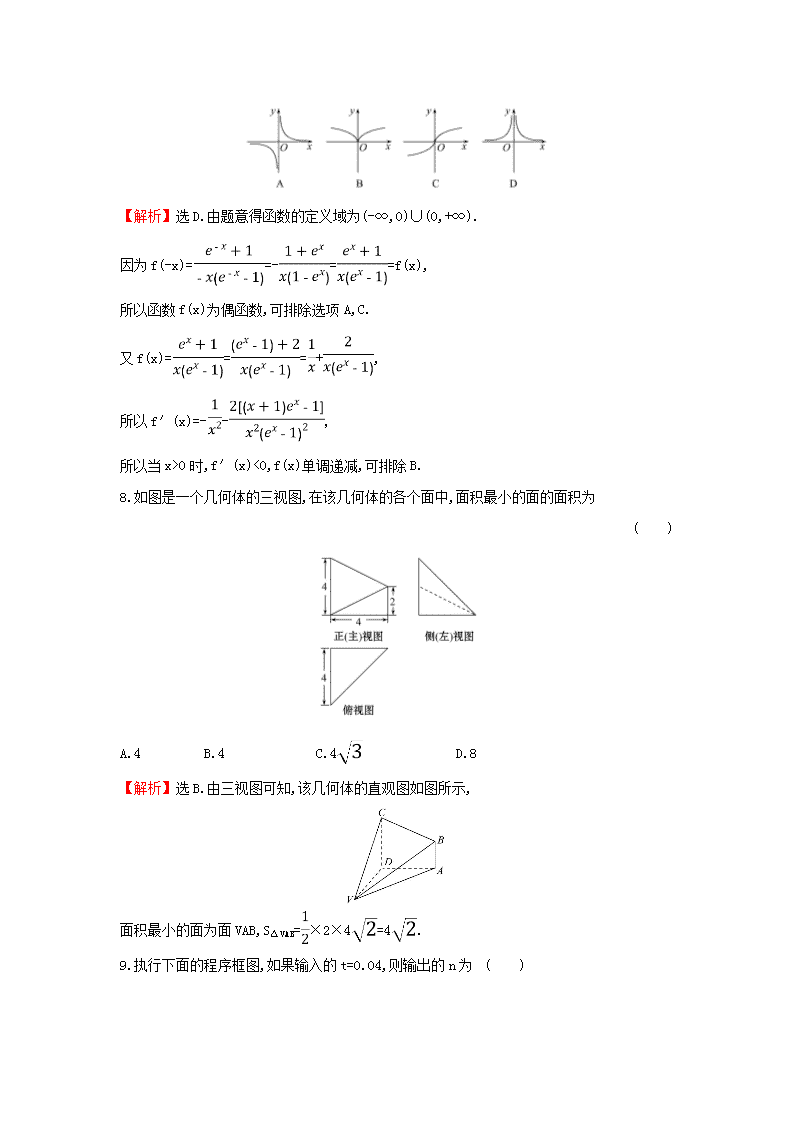
8.如图是一个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为
( )
A.4 B.4 C.4 D.8
【解析】选B.由三视图可知,该几何体的直观图如图所示,
面积最小的面为面VAB,S△VAB=×2×4=4.
9.执行下面的程序框图,如果输入的t=0.04,则输出的n为 ( )
A.7 B.6 C.5 D.4
【解析】选C.第一次执行循环体后,s=,m=,n=1,满足条件,第二次执行循环体后,s=,m=,n=2,满足条件,第三次执行循环体后,s=,m=,n=3,满足条件,第四次执行循环体后,s=,m=,n=4,满足条件,第五次执行循环体后,s=,m=,n= 5,由于s==0.031 25<0.04,不满足条件,输出n=5.
10.已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在的平面互相垂直,AB=3,AC=,BC=CD=BD=2,则球O的表面积为( )
A.4π B.12π C.16π D.36π
【解析】选C.如图所示,
因为AB2+AC2=BC2,
所以∠CAB为直角,即过△ABC的小圆面的圆心为BC的中点O′,△ABC和△DBC所在的平面互相垂直,则球心在过△DBC的圆面上,即△DBC的外接圆为球的大圆,由等边三角形的重心和外心重合易得球半径R=2,球的表面积为S=4πR2=16π.
11.在非等腰△ABC中,内角A,B,C所对的边分别为a,b,c,sin A(2cos B-a)=
sin B(2cos A-b),则c=( )
A. B.1 C.2 D.
【解析】选C.因为sin A(2cos B-a)=sin B(2cos A-b),
所以2sin Acos B-2sin Bcos A=asin A-bsin B,
由正弦定理可得2acos B-2bcos A=a2-b2
由余弦定理得2a×-2b×=a2-b2,
即-=a2-b2,
即=a2-b2,因为a≠b,所以c=2.
12.定义运算:x☉y=则☉cos2α+sin α-的最大值为 ( )
A.4 B.3 C.2 D.1
【解析】选D.令f(α)=cos2α+sin α-=1-sin2α+sin α-=-+1,
由于sin α∈[-1,1],
所以f(α)∈⇒f(α)>-,
所以☉=cos2 α+sin α-,所以其最大值为1.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.下表是某工厂1~4月份用水量(单位:百吨):
月份x
1
2
3
4
用水量y
5.5
4
3.5
3
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程=-0.4x+b,则b=________.
【解析】由表中数据可知:==,==4.
又=-0.4+b,所以b=4+0.4×=5.
答案:5
14.已知函数f(x)=cos2x+sin xcos x,x∈0,,则f(x)的单调递增区间为________.
【解析】f(x)=cos2x+sin xcos x=+sin 2x=sin2x++,根据正弦函数的单调性可得2kπ-≤2x+≤2kπ+,解得kπ-≤x≤kπ+(k∈Z),又x∈0,,所以f(x)的单调递增区间为0,(或0,).
答案:0,(或0,)
15.椭圆+=1(a>b>0),直线l1:y=-x,直线l2:y=x,P为椭圆上任意一点,过P作PM∥l1且与直线l2交于点M,作PN∥l2且与l1交于点N,若|PM|2+|PN|2为定值,则椭圆的离心率为________.
【解析】令|PM|2+|PN|2=t(t为常数),设Mx1,x1,Nx2,-x2,由平行四边形知识,|PM|2+|PN|2=|OM|2+|ON|2=(+)=t,
设点P(x,y),
因为=+=x1+x2,x1-x2,所以⇒x2+4y2=2(+)=t,此方程即为椭圆方程,即e=.
答案:
16.P为椭圆C:+y2=1上一动点,F1,F2分别为左、右焦点,延长F1P至点Q,使得|PQ|=|PF2|,记动点Q的轨迹为Ω,设点B为椭圆C短轴上一顶点,直线BF2与Ω交于M,N两点,则|MN|=________.
【解析】因为|PF1|+|PF2|=2a=2,|PQ|=|PF2|,
所以|PF1|+|PQ|=|QF1|=2.动点Q的轨迹为Ω,为以F1为圆心,半径为2的圆,
因为|BF1|=|BF2|=.|F1F2|=2,所以BF1⊥BF2,则|MN|=2=2.
答案:2