2020届二轮复习集合与简易逻辑

2020届二轮复习集合与简易逻辑

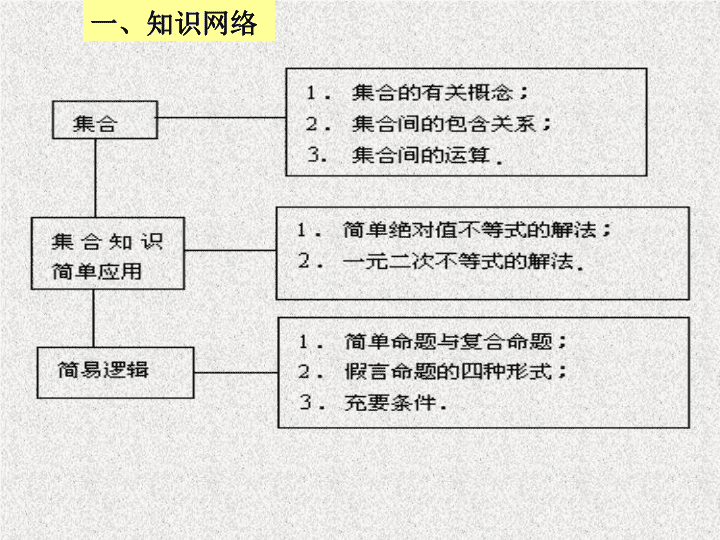
集合与简易逻辑 成功的秘诀就是四个简单的字：多一点点。 凡事比别人多一点点！多一点努力，多一点自律，多一点实践，多一点疯狂。多一点点就能创造奇迹！ 一、知识网络 分析：集合 M 、 N 分别表示向量集合，先认清这两个向量集合，再找它们的公共向量。 归纳点评 　解答集合问题，必须弄清题目的要求，正确理解各个集合的含义，再对集合进行简化，借助数轴或韦恩图进而使问题得到解决。 二、例题剖析 练 1 、已知集合 M={y|y=x 2 +1 ， x∈R} ， N={y|y=x+1 ， x∈R} ，求 M∩N . ， ， ，则集合 练 2 、设集合 中元素的个数为（ ） A.1 B. 2 C.3 D.4 注意全集与补集的含义，集合中元素的互异性。 例 2 、已知集合 ，若 求 a 的值。 分析：去掉绝对值符号的方法（定义法，公式法，平方法，零点分段法）； 　解分式不等式基本方法：右边化零法，相除化相乘； 　解一元二次不等式基本方法：分解因式法等 . 的解集可用 P 、 Q 表示为 . 练 4 、若全集 I =R ， f （ x ）、 g （ x ）均为 x 的二次函数， P ={ x | f ( x ) ＜ 0} ， Q ={ x | g ( x )≥0} ，则不等式组 例 3 、已知 h>0 ，设命题甲：两个实数 a,b 满足 |a-b|<2h ，命题乙：两个实数 a,b 满足 |a-1|

查看更多