- 2021-05-24 发布 |
- 37.5 KB |
- 14页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习(理)专题跟踪训练21空间几何体的三视图、表面积与体积作业(全国通用)
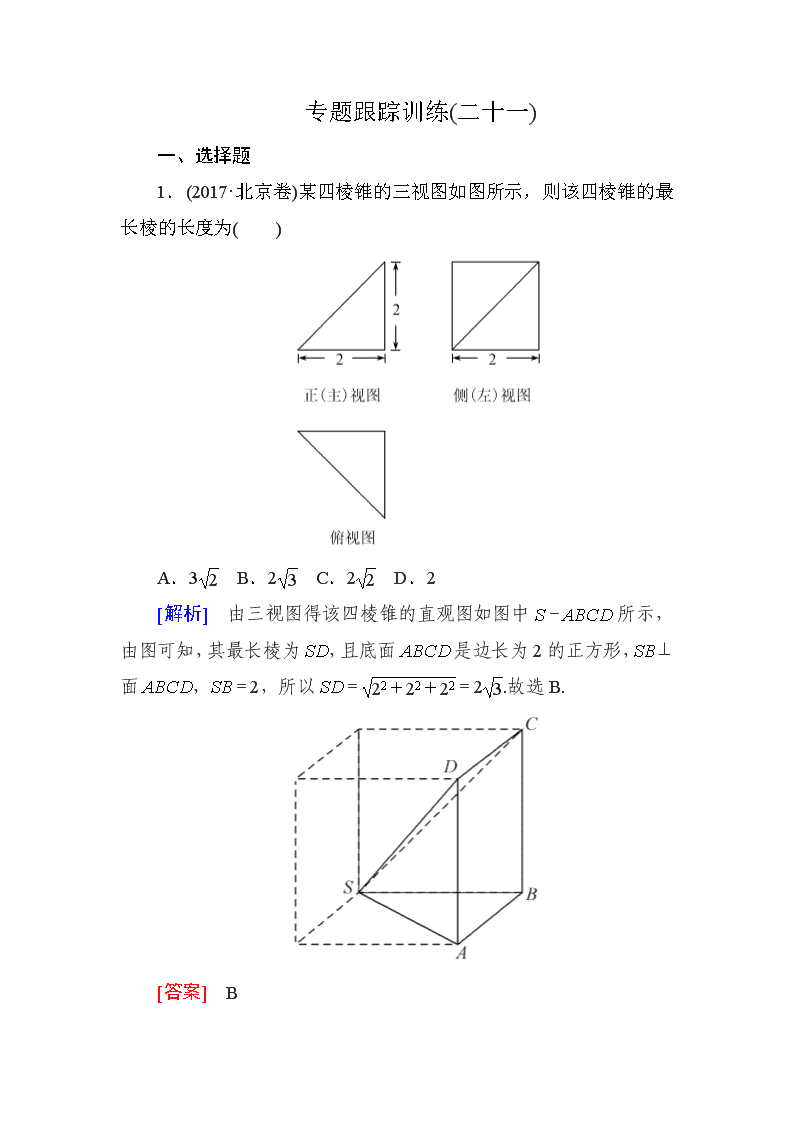
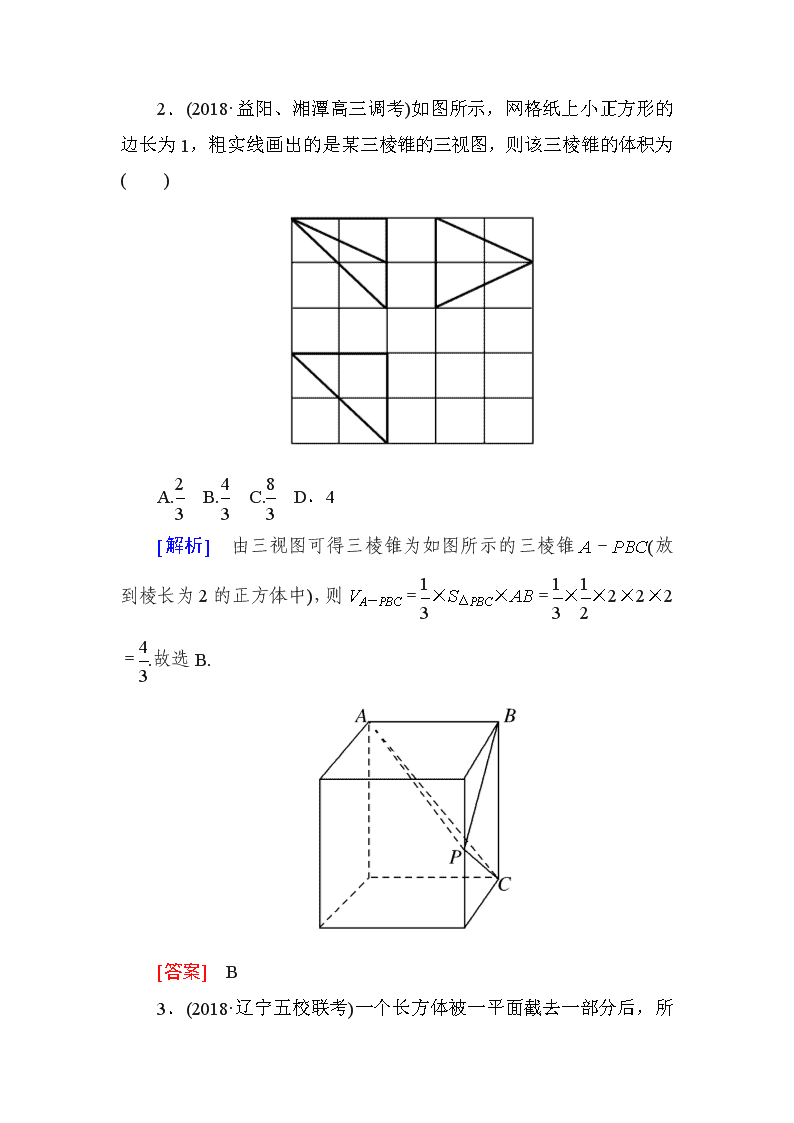
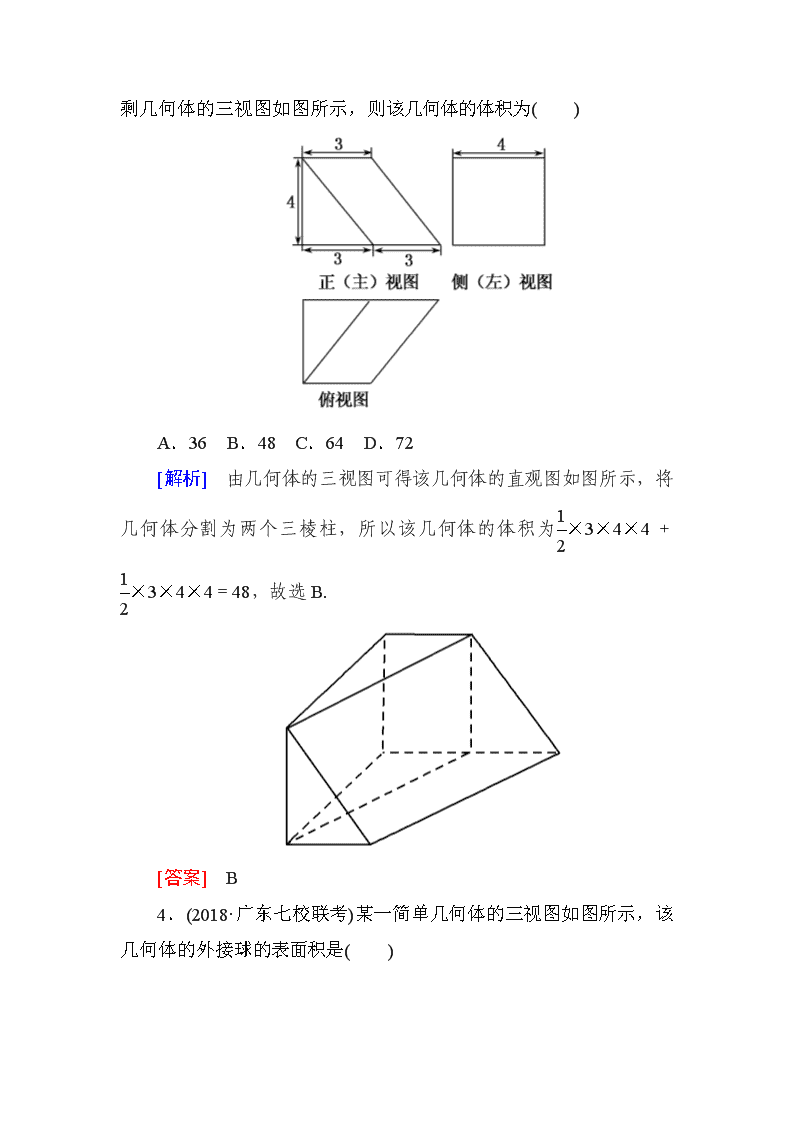
专题跟踪训练(二十一) 一、选择题 1.(2017·北京卷)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( ) A.3 B.2 C.2 D.2 [解析] 由三视图得该四棱锥的直观图如图中S-ABCD所示,由图可知,其最长棱为SD,且底面ABCD是边长为2的正方形,SB⊥面ABCD,SB=2,所以SD==2.故选B. [答案] B 2.(2018·益阳、湘潭高三调考)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某三棱锥的三视图,则该三棱锥的体积为( ) A. B. C. D.4 [解析] 由三视图可得三棱锥为如图所示的三棱锥A-PBC(放到棱长为2的正方体中),则VA-PBC=×S△PBC×AB=××2×2×2=.故选B. [答案] B 3.(2018·辽宁五校联考)一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( ) A.36 B.48 C.64 D.72 [解析] 由几何体的三视图可得该几何体的直观图如图所示,将几何体分割为两个三棱柱,所以该几何体的体积为×3×4×4+×3×4×4=48,故选B. [答案] B 4.(2018·广东七校联考)某一简单几何体的三视图如图所示,该几何体的外接球的表面积是( ) A.13π B.16π C.25π D.27π [解析] 由三视图知该几何体是一个底面为正方形的长方体,由正视图知该长方体的底面正方形的对角线长为4,所以底面边长为2,由侧视图知该长方体的高为3,设该几何体的外接球的半径为R,则2R==5,解得R=,所以该几何体的外接球的表面积S=4πR2=4π×=25π,故选C. [答案] C 5.(2018·洛阳市高三第一次联考)已知球O与棱长为4的正四面体的各棱相切,则球O的体积为( ) A.π B.π C.π D.π [解析] 将正四面体补成正方体,则正四面体的棱为正方体相应面上的对角线,因为正四面体的棱长为4,所以正方体的棱长为2.因为球O与正四面体的各棱都相切,所以球O为正方体的内切球,即球O的直径为正方体的棱长,其长为2,则球O的体积V=πR3= π,故选A. [答案] A 6.(2018·河北第二次质检)《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱.已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( ) A.50 B.75 C.25.5 D.37.5 [解析] 由题意及给定的三视图可知,剩余部分是在直三棱柱的基础上,截去一个四棱锥所得的,且直三棱柱的底面是腰长为5的等腰直角三角形,高为5.如图,图中几何体ABCC1MN为剩余部分,因为AM=2,B1C1⊥平面MNB1A1,所以剩余部分的体积V=V三棱柱-V四棱锥=×5×5×5-×3×5×5=37.5,故选D. [答案] D 7.(2018·广东广州调研)如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的表面积为( ) A.4+4+2 B.14+4 C.10+4+2 D.4 [解析] 如图,该几何体是一个底面为直角梯形,有一条侧棱垂直于底面的四棱锥S-ABCD.连接AC,因为AC==2,SC==2,SD=SB==2,CD==2,SB2+BC2=(2)2+42=24=SC2,故△SCD为等腰三角形,△SCB为直角三角形.过D作DK⊥SC于点K,则DK==,△SCD的面积为× ×2=2,△SBC的面积为×2×4=4.所求几何体的表面积为×(2+4)×2+2××2×2+4+2=10+4+2,选C. [答案] C 8.(2018·河南濮阳二模)已知三棱锥A-BCD中,△ABD与△BCD是边长为2的等边三角形且二面角A-BD-C为直二面角,则三棱锥A-BCD的外接球的表面积为( ) A. B.5π C.6π D. [解析] 取BD中点M,连接AM,CM,取△ABD,△CBD的中心即AM,CM的三等分点P,Q,过P作面ABD的垂线,过Q作面CBD的垂线,两垂线相交于点O,则点O为外接球的球心,其中OQ=,CQ=,连接OC,则外接球的半径R=OC=,表面积为4πR2=,故选D. [答案] D 9.(2018·广东揭阳一模)某几何体三视图如图所示,则此几何体的表面积为( ) A.4π+16 B.2(+2)π+16 C.4π+8 D.2(+2)π+8 [解析] 由三视图知,该几何体是一个棱长为2的正方体和一个底面半径为、高为1的圆柱的组合体,其表面积S表=5×22+2π··1+2π·()2-22=2(+2)π+16.故选B [答案] B 10.(2018·福建福州质检)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,俯视图中的两条曲线均为圆弧,则该几何体的体积为( ) A.64- B.64-8π C.64- D.64- [解析] 由三视图可知该几何体是由棱长为4的正方体截去个圆锥和个圆柱所得到的,且圆锥的底面半径为2,高为4,圆柱的底面半径为2,高为4,所以该几何体的体积为43-=64-.故选C. [答案] C 11.(2018·湖南十三校联考)三棱锥S-ABC及其三视图中的正视图和侧视图如下图所示,则该三棱锥S-ABC的外接球的表面积为( ) A.32π B.π C.π D.π [解析] 设外接球的半径为r,球心为O.由正视图和侧视图可知,该三棱锥S-ABC的底面是边长为4的正三角形.所以球心O一定在△ABC的外心上方.记球心O在平面ABC上的投影点为点D,所以AD=BD=CD=4××=,则由题可建立方程 +=4,解得r2=.所以该三棱锥S-ABC的外接球的表面积S=4πr2=π.故选B. [答案] B 12.(2018·中原名校联考)已知A,B,C,D是球O表面上四点,点E为BC的中点,点AE⊥BC,DE⊥BC,∠AED=120°,AE=DE=,BC=2,则球O的表面积为( ) A.π B. C.4π D.16π [解析] 由题意可知△ABC与△BCD都是边长为2的正三角形,如图,过△ABC与△BCD的外心M,N分别作面ABC、面BCD 的垂线,两垂线的交点就是球心O. 连接OE,可知∠MEO=∠NEO=∠AED=60°, 在Rt△OME中,∠MEO=60°,ME=,所以OE=2ME=,连接OB,所以球O的半径R=OB===,所以球O的表面积为S=4πR2=π,故选B. [答案] B 二、填空题 13.(2018·沈阳质检)三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则的值为________. [解析] 如图,设S△ABD=S1,S△PAB=S2,E到平面ABD的距离为h1,C到平面PAB的距离为h2,则S2=2S1,h2=2h1,V1=S1h1,V2=S2h2,所以==. [答案] 14.(2018·宁夏银川一中模拟)如图为某几何体的三视图,则该几何体的体积为________. [解析] 由三视图知,该几何体是一个高为2,底面直径为2的圆柱被一平面从上底面最右边缘斜向下45°切开所剩下的几何体,其体积为对应的圆柱的体积的一半,即V=×π×12×2=π.故答案为π. [答案] π 15.已知某几何体的三视图如图所示,则该几何体最长的棱长为________. [解析] 依题意知,几何体是如图所示的三棱锥A-BCD.其中∠CBD=120°,BD=2,点C到直线BD的距离为,BC=2,CD=2,AB=2,AB⊥平面BCD,因此AC=AD=2,所以该几何体最长的棱长为2. [答案] 2. 16.(2018·厦门一模)如图所示的是一个几何体的三视图, 则该几何体的表面积为________. [解析] 该几何体为一个长方体从正上方挖去一个半圆柱剩下的部分,长方体的长、宽、高分别为4,1,2,挖去半圆柱的底面半径为1,高为1,所以表面积为S=S长方体表-S半圆柱底-S圆柱轴截面+S半圆柱侧=2×4×1+2×1×2+2×4×2-π×12-2×1+×2π×1=26. [答案] 26查看更多