- 2021-05-24 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小升初分班奥数平面图形面积
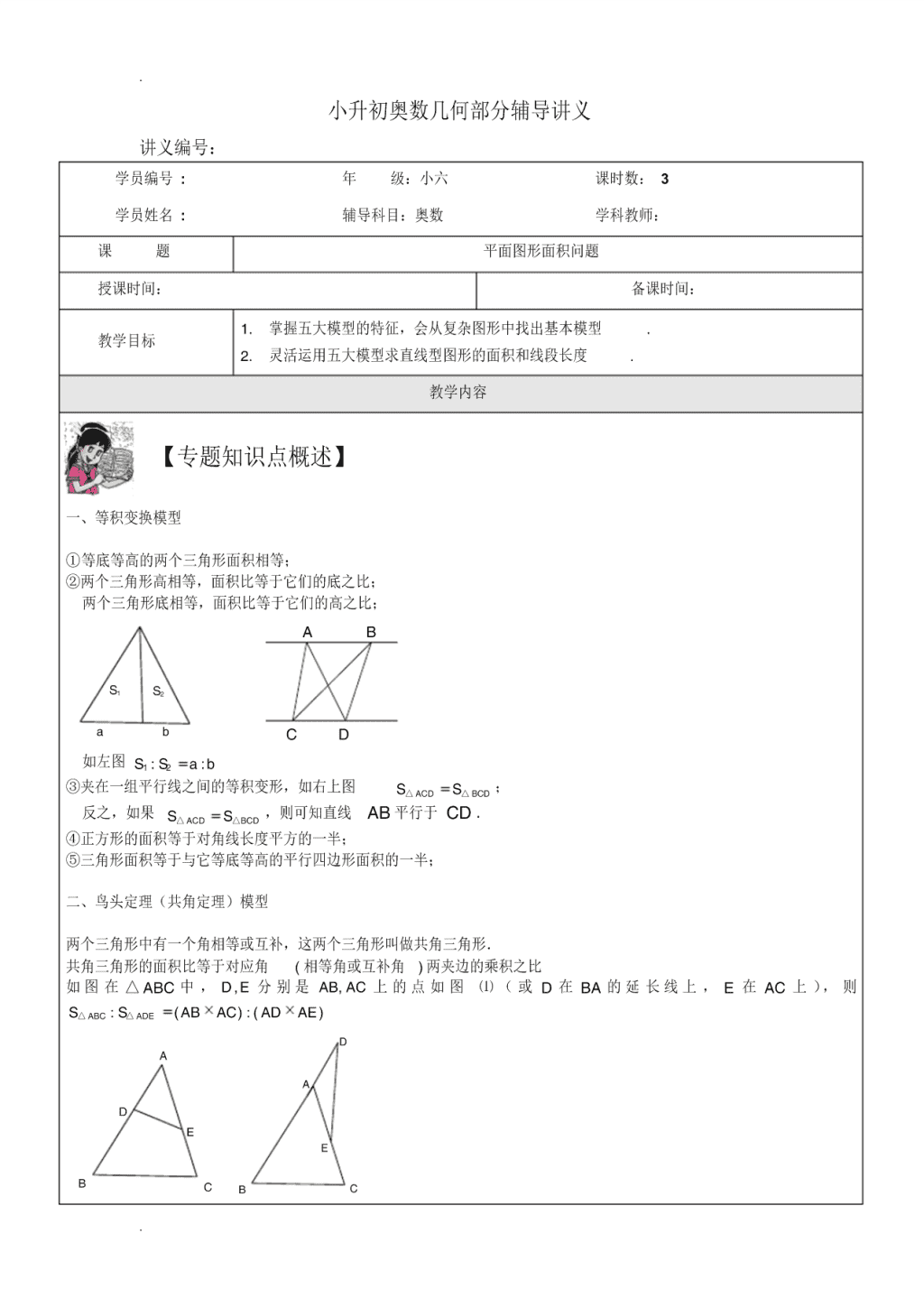
. . 小升初奥数几何部分辅导讲义 讲义编号: 学员编号 : 年 级:小六 课时数: 3 学员姓名 : 辅导科目:奥数 学科教师: 课 题 平面图形面积问题 授课时间: 备课时间: 教学目标 1. 掌握五大模型的特征,会从复杂图形中找出基本模型 . 2. 灵活运用五大模型求直线型图形的面积和线段长度 . 教学内容 【专题知识点概述】 一、等积变换模型 ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; ba S2S1 DC BA 如左图 1 2: :S S a b ③夹在一组平行线之间的等积变形,如右上图 ACD BCDS S△ △ ; 反之,如果 ACD BCDS S△ △ ,则可知直线 AB 平行于 CD . ④正方形的面积等于对角线长度平方的一半; ⑤三角形面积等于与它等底等高的平行四边形面积的一半; 二、鸟头定理(共角定理)模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角 ( 相等角或互补角 ) 两夹边的乘积之比 如 图 在 ABC△ 中 , ,D E 分 别 是 ,AB AC 上 的 点 如 图 ⑴ ( 或 D 在 BA 的 延 长 线 上 , E 在 AC 上 ), 则 : ( ) : ( )ABC ADES S AB AC AD AE△ △ E D CB A E D CB A . . 图⑴ 图⑵ 推理过程连接 BE ,再利用等积变换模型即可 三、蝴蝶定理模型 任意四边形中的比例关系 ( “蝴蝶定理” ) : S4 S3 S2 S1 O D CB A ① 1 2 4 3: :S S S S 或者 1 3 2 4S S S S ② 1 2 4 3: :AO OC S S S S 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形 的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系 ( “梯形蝴蝶定理” ) : A B C D O b a S3 S2 S1 S4 ① 2 2 1 3: :S S a b ② 2 2 1 3 2 4: : : : : :S S S S a b ab ab ; ③梯形 S 的对应份数为 2 a b . 四、相似模型 相似三角形性质: G F E A B C D (金字塔模型) A B C DE F G (沙漏模型) . . ① AD AE DE AF AB AC BC AG ; ② 2 2:ADE ABCS S AF AG△ △: . 所谓的相似三角形,就是形状相同,大小不同的三角形 ( 只要其形状不改变,不论大小怎样改变它们都相似 ) , 与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; 五、燕尾定理模型 S△ABG : S△AGC S△ BGE : S△EGC BE : EC; S△BGA : S△BGC S△ AGF : S△FGC AF : FC; S△AGC : S△BCG S△ ADG : S△ DGB AD : DB ; 【习题精讲】 【例 1】(难度等级 ※※) 用四种不同的方法,把任意一个三角形分成四个面积相等的三角形. 【例 2】(难度等级 ※※) 如右图,已知在△ ABC中, BE=3AE,CD=2AD.若△ ADE的面积为 1 平方厘米.求三角形 ABC的面积. 【例 3】(难度等级 ※※) 如图,长方形 ABCD 的面积是 56平方厘米,点 E 、 F 、 G 分别是长方形 ABCD 边上的中点, H 为 AD 边上的任 意一点,求阴影部分的面积. G F E D CB A . . H G F E D CB A 【例 4】(难度等级 ※※) 如图,在三角形 ABC中,,D 为 BC的中点, E 为 AB上的一点,且 BE=1 3 AB,已知四边形 EDCA的面积是 35,求三 角形 ABC的面积 . 【例 5】(难度等级 ※※) (2008 年四中考题 ) 如右图, AD DB , AE EF FC ,已知阴影部分面积为 5 平方厘米, ABC 的面积是 平方厘米. FE D C B A 【举一反三】(难度等级 ※※) 如右图,在平行四边形 ABCD中, E、 F 分别是 AC、BC的三等分点,且 SABCD=54平方厘米,求 S△BEF. 【例 6】(难度等级 ※※※) 图 30-10 是一个正方形,其中所标数值的单位是厘米.问:阴影部分的面积是多少平方厘米 ? . . 【例 7】(难度等级 ※※) 如图在 ABC△ 中, ,D E 分别是 ,AB AC 上的点,且 : 2:5AD AB , : 4:7AE AC , 16ADES△ 平方厘米,求 ABC△ 的面积. E D CB A 【举一反三】(难度等级 ※※) 如图,三角形 ABC 中, AB 是 AD 的 5 倍, AC 是 AE 的 3 倍,如果三角形 ADE 的面积等于 1,那么三角形 ABC 的面积是多少? ED CB A 【例 8】(难度等级 ※※) 如图在 ABC△ 中, D 在 BA的延长线上, E 在 AC 上,且 : 5: 2AB AD , : 3: 2AE EC , 12ADES△ 平方厘 米,求 ABC△ 的面积. E D CB A 【例 9】(难度等级 ※※) 如图所示,在平行四边形 ABCD 中, E 为 AB 的中点, 2AF CF ,三角形 AFE( 图中阴影部分 ) 的面积为 8 平方 厘米.平行四边形的面积是多少平方厘米? E F D C BA 【例 10 】(难度等级 ※※※) 已知 DEF△ 的面积为 7 平方厘米, , 2 , 3BE CE AD BD CF AF ,求 ABC△ 的面积. . . F E D C B A 【例 11 】(难度等级 ※※※) ( 2007 年”走美”五年级初赛试题 ) 如图所示, 正方形 ABCD 边长为 6 厘米, 1 3 AE AC , 1 3 CF BC .三角形 DEF 的面积为 _______平方厘米. F E D CB A 【例 12 】(难度等级 ※※※) 如图,在 ABC△ 中,延长 AB 至 D ,使 BD AB ,延长 BC至 E ,使 1 2 CE BC , F 是 AC 的中点,若 ABC△ 的 面积是 2 ,则 DEF△ 的面积是多少? A B C D E F 【例 13 】(难度等级 ※※※) 如图所示,已知 1. , 2 .ABCS AE ED BD DC 求图中阴影部分的面积 . 【举一反三】(难度等级 ※※※) 下图中阴影部分甲的面积与阴影部分乙的面积哪个大? . . 【例 14 】(难度等级 ※※※) 右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为 15、18、 30 公顷,问图 中阴影部分的面积是多少? 【例 15 】(难度等级 ※※※) 梯形 ABCD的上底长为 3 厘米,下底长为 9 厘米,而三角形 ABO的面积为 12 平方厘米。则整个梯形的面积为多少? 【例 16 】(难度等级 ※※※) 在图中,正方形 ADEB和正方形 ECFG底边对齐,两个正方形边长分别为 6 和 4.三角形 ACG和三角形 BDF的面积 分别是多少? 【例 17 】(难度等级 ※※※) 如右图,梯形 ABCD 的面积是 45 平方米,高 6 米,△ AED 的面积是 5 平方米, BC=10 米,求阴影部分面积 . . . 【例 18 】(难度等级 ※※※) 在ΔABC中 BD:DC=2:1,AE: EC=1:3 求 BO:OE。 【例 19 】(难度等级 ※※※) 图中的四边形土地总面积为 52 公顷,两条对角线把它分成了 4 个小三角形,其中 2 个小三角形的面积分别是 6 公顷和 7 公顷。那么最大的一个三角形的面积是多少公顷? 【例 20 】(难度等级 ※※※) 梯形 ABCD 被两条对角线分成了四个三角形 S1 、S2、S3、S 4。已知 S 1 =2 厘米 2 ,S2 =6 厘米 2 。求梯形 ABCD 的面积。(小学数学奥林匹克通讯赛决赛试题) 【例 21 】(难度等级 ※※※) 右图中 ABCD是梯形, ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米) ,阴影部分的面积是多 少平方厘米? 【例 22 】(难度等级 ※※※) 如下图,已知 ABCD是长方形, A、D、E 和 F 在一条直线上, AB=7, BC=5, DG=3。(单位:厘米),求 DE的 长。 O A B D C E . . 【例 23 】(难度等级 ※※※) 将三角形 ABC的 BA边延长 1 倍到 D;CB边延长 2 倍到 E,AC边延长 3 倍到 F,如果三角形 ABC的面积等于 1,那 么三角形 DEF的面积是多少?( 08 年三帆考题) 【作业】 1、如图,三角形 ABC 被分成了甲 ( 阴影部分 ) 、乙两部分, 4BD DC , 3BE , 6AE ,乙部分面积是甲部 分面积的几倍? 乙 甲 E D CB A 2、已知三角形 ABC 的面积为 1,BE=2AB , BC=CD ,求三角形 BDE 的面积? 3、如右图,在梯形 ABCD中, AC与 BD是对角线,其交点 O,求证:△ AOB与△ COD面积相等. . . 4、如右图,已知在△ ABC中, BE=3AE,CD=2AD.若△ ADE的面积为 1 平方厘米.求三角形 ABC的面积. 5、一块长方形的土地被分割成 4 个小长方形,其中三块的面积如图所示(单位:平方米) ,剩下一块的面积应该 是多少平方米? 6. 下图中大正方形的边长为 3 厘米,小正方形的边长为 2 厘米,求阴影部分的面积。 7、如右图所示,已知三角形 ABC面积为 1,延长 AB至 D,使 BD=AB;延长 BC至 E,使 CE=2BC;延长 CA至 F,使 AF=3AC,求三角形 DEF的面积。 8、如下图,已知 D是 BC的中点, E 是 CD的中点, F 是 AC的中点,且 ADG 的面积比 EFG 的面积大 6 平方 厘米。 ?的面积是多少平方厘米ABC A B CD E F G . .查看更多