- 2021-05-24 发布 |
- 37.5 KB |
- 34页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
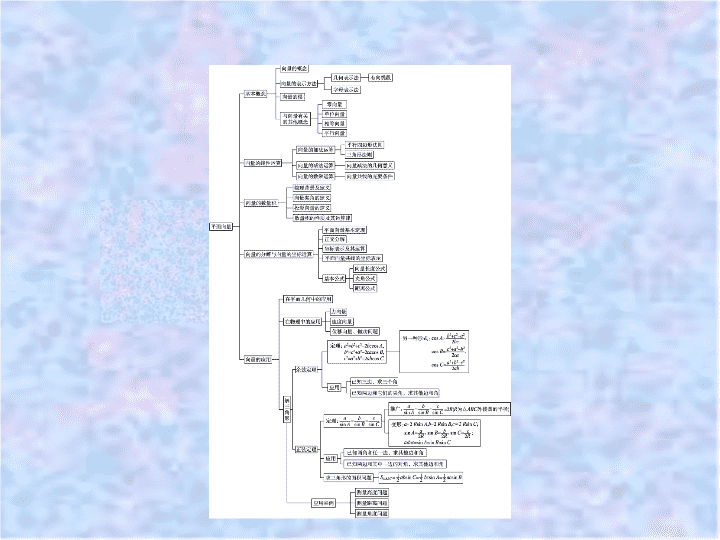
【新教材】2020-2021学年高中人教A版数学必修第二册课件:第六章 章末整合
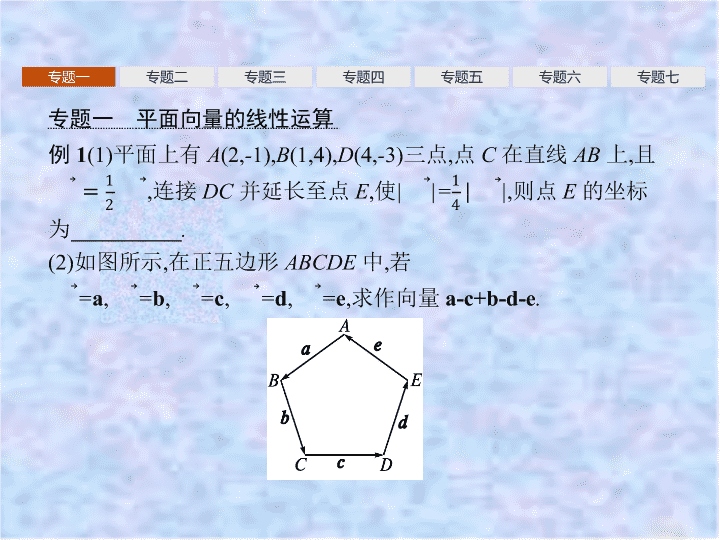
章 末整合 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 平面向量的线性运算 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 向量加法的平行四边形法则要点是 “ 共起点 ”, 则共起点对角线的向量即为向量的和 . 向量加法满足交换律、结合律 . 2 . 向量减法实质是向量加法的逆运算 , 是相反向量的作用 . 几何意义有两个 : 一是以减向量的终点为起点 , 被减向量的终点为终点的向量 ; 二是加法的平行四边形法则的另外一条对角线的向量 . 注意两向量要移至共起点 . 3 . 数乘运算即通过实数与向量的乘积 , 实现同向或反向上向量长度的伸缩变换 . 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题二 平面向量数量积的运算 专题一 专题二 专题三 专题四 专题五 专题六 专题七 名师点析 向量数量积的求解策略 (1) 利用数量积的定义、运算律求解 . 在数量积运算律中 , 有两个形似实数的完全平方公式在解题中的应用较为广泛 , 即 ( a+b ) 2 =a 2 + 2 a · b+b 2 ,( a-b ) 2 =a 2 - 2 a · b+b 2 , 上述两公式以及 ( a+b ) · ( a-b ) =a 2 -b 2 这一类似于实数平方差的公式在解题过程中可以直接应用 . (2) 借助零向量 . 即借助 “ 围成一个封闭图形且首尾相接的向量的和为零向量 ”, 再合理地进行向量的移项以及平方等变形 , 求解数量积 . (3) 借助平行向量与垂直向量 . 即借助向量的拆分 , 将待求的数量积转化为有垂直向量关系或平行向量关系的向量数量积 , 借助 a ⊥ b , 则 a · b = 0 等解决问题 . (4) 建立坐标系 , 利用坐标运算求解数量积 . 专题一 专题二 专题三 专题四 专题五 专题六 专题七 答案 : D 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题三 平面向量的平行与垂直问题 例 3 (1) 已知向量 m = ( λ + 1,1), n = ( λ + 2,2), 若 ( m+n ) ⊥ ( m-n ), 则 λ = ( ) A. - 4 B. - 3 C. - 2 D. - 1 (2) 设 A , B , C , D 为平面内的四点 , 且 A (1,3), B (2, - 2), C (4,1 ) . (1) 解析 : 因为 m+n = (2 λ + 3,3), m-n = ( - 1, - 1), 且 ( m+n ) ⊥ ( m-n ), 所以 ( m+n )·( m-n ) =- 2 λ - 3 - 3 = 0, 解得 λ =- 3 . 故选 B . 答案 : B 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 名师点析 1 . 证明向量共线问题常用的方法 (1) 向量 a , b ( a ≠0) 共线 ⇔ 存在唯一实数 λ , 使 b = λ a . (2) 向量 a = ( x 1 , y 1 ), b = ( x 2 , y 2 ) 共线 ⇔ x 1 y 2 -x 2 y 1 = 0 . (3) 向量 a 与 b 共线 ⇔ |a · b|=|a||b| . (4) 向量 a 与 b 共线 ⇔ 存在不全为零的实数 λ 1 , λ 2 , 使 λ 1 a + λ 2 b = 0 . 2 . 证明平面向量垂直问题的常用方法 a ⊥ b ⇔ a · b = 0 ⇔ x 1 x 2 +y 1 y 2 = 0, 其中 a = ( x 1 , y 1 ), b = ( x 2 , y 2 ) . 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题四 平面向量的模、夹角 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题一 专题二 专题三 专题四 专题五 专题六 专题七 名师点析 1 . 解决向量模的问题常用的策略 ( 2) 应用三角形或平行四边形法则 . (3) 应用向量不等式 ||a|-|b|| ≤ |a±b| ≤ |a|+|b| . (4) 应用模的平方 |a±b| 2 = ( a±b ) 2 . 2 . 求向量的夹角 设非零向量 a = ( x 1 , y 1 ), b = ( x 2 , y 2 ), 两向量夹角 θ (0≤ θ ≤ π ) 的余弦 值 专题一 专题二 专题三 专题四 专题五 专题六 专题七 答案 : C 专题一 专题二 专题三 专题四 专题五 专题六 专题七 专题五 利用正弦定理、余弦定理解三角形 例 5 在 △ ABC 中 , 内角 A , B , C 所对的边分别为 a , b , c. 已知 b+c= 2 a cos B. (1) 求证 : A= 2 B ; (2) 若 △ ABC 的面积 S = , 求角 A 的大小 . (1) 证明 : 由正弦定理得 sin B+ sin C= 2sin A cos B , 故 2sin A cos B= sin B+ sin( A+B ) = sin B+ sin A cos B+ cos A sin B , 于是 sin B= sin( A-B ) . 又 A , B ∈ (0, π ), 故 0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档