【数学】江西省上饶市横峰中学2020-2021学年高二上学期第一次月考（文）

【数学】江西省上饶市横峰中学2020-2021学年高二上学期第一次月考（文）

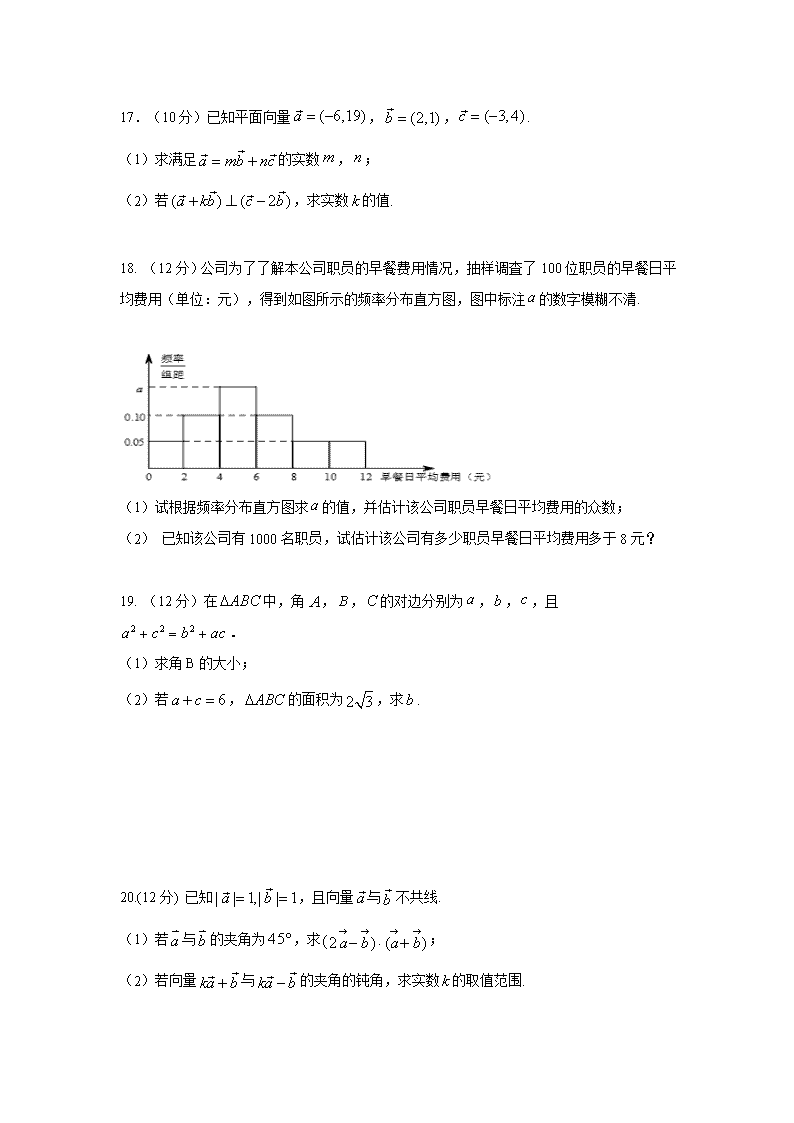
江西省上饶市横峰中学2020-2021学年 高二上学期第一次月考（文）‎ 命题人: 审题人： 满分：150分 一、选择题：（本题包括12小题，每小题5分，共60分，每小题只有一个选项符合题意）‎ ‎1.已知向量，，则下列结论正确的是（ ） ‎ A． B．// C． D．‎ ‎2. 已知平面向量，且，则（ ）‎ A． B． C． D．‎ ‎3. 在中，角A、B、C所对的边分别为a、b、c ,，，，则 ( )‎ A．1 B． C． D．2‎ ‎4.为了解某高中学生的身高情况，现采用分层抽样的方法从三个年级中抽取一个容量为100的样本，其中高一年级抽取24人，高二年级抽取26人．若高三年级共有学生600人，则该校学生总人数为（ ）‎ A．900 B．1200 C．1500 D．1800‎ ‎5. 中，分别是角的对边，若则的外接圆的面积是（ ）‎ A． B． C． D． ‎ ‎6.中，，．若点满足，则（ ）‎ A． B．C． D．‎ ‎7. 如表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y（吨标准煤）的几组对应数据，根据表中提供的数据，求出y关于x的线性回归方程y=0.7x+0.35，那么表中m的值为（ ）‎ ‎ x ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 6 ‎ ‎ y ‎ 2.5‎ ‎ m ‎ 4‎ ‎ 4.5‎ A．4 B．3.15 C．4.5 D．3‎ ‎8.在中，角A、B、C所对的边分别为a、b、c，且若，则的形状是（ ）‎ A．等腰三角形 B．直角三角形 C．等边三角形 D．等腰直角三角 ‎9.已知,，的夹角为120°，则向量与向量的夹角为( ）‎ A．60° B．120° C．30° D．150°‎ ‎10.中，角对应的边分别为，，，则的值为（ ）‎ A． B． C． D．‎ ‎11.已知是两个单位向量，时，的最小值为，则=（ ）‎ A．1 B． C．1或 D．2‎ ‎12. 设分别是的内角A，B，C的对边，已知D是BC边的中点，且，则等于（ ）‎ A． B． C． D．‎ 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13. 已知，，且//，则实数k =________．‎ ‎14. 已知，，且，则向量在方向上的投影为 .‎ ‎15. 在中，分别为的对边，，这个三角形的面积为，则 .‎ ‎16. 的内角的对边分别为，已知，，则面积的最大值为_ .‎ 三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17．（10分）已知平面向量，，.‎ ‎（1）求满足的实数，；‎ ‎（2）若，求实数的值.‎ ‎18. （12分）公司为了了解本公司职员的早餐费用情况，抽样调査了100位职员的早餐日平均费用（单位：元），得到如图所示的频率分布直方图，图中标注的数字模糊不清.‎ ‎（1）试根据频率分布直方图求的值，并估计该公司职员早餐日平均费用的众数；‎ ‎（2） 已知该公司有1000名职员，试估计该公司有多少职员早餐日平均费用多于8元？‎ ‎19. （12分）在中，角，，的对边分别为，，，且．‎ ‎（1）求角B的大小；‎ ‎（2）若，的面积为，求.‎ ‎20.(12分) 已知，且向量与不共线.‎ ‎（1）若与的夹角为，求；‎ ‎（2）若向量与的夹角的钝角，求实数的取值范围.‎ ‎21．（12分）在中，角，，的对边分别为，，C已知向量，，且．‎ ‎（1）求角的大小；‎ ‎（2）若，求面积．‎ ‎22．（12分）在锐角三角形中，角所对的边分别为，已知.‎ ‎（1）求角的大小； （2）求的取值范围.‎ 参考答案 一、选择题：（本题包括12小题，每小题5分，共60分）‎ ‎1-12、CBABAA DCBBCC 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13.-6 14. 15. 16. ‎ 三、解答题(本大题共6小题，共70分)‎ ‎17.（10分）解：（1）由，得：‎ 且 所以 得，.‎ ‎（2）因为，，‎ 且，‎ 所以，‎ 所以.‎ ‎18. （12分）解：（1）因为频率分布直方图中各小长方形的面积之和为1，‎ 所以，解得；‎ 该公司职员早餐日平均费用的众数为；‎ ‎（2）由频率分布直方图可知，‎ 职员早餐日平均费用不少于8元的频率为，‎ 又因为该公司有1000名职员，‎ 所以该公司职员早餐日平均费用不少于8元的有（人）.‎ ‎19.（12分）解：（1）因为，由余弦定理，，所以，‎ 因为，所以；‎ ‎（2），所以，因为，即，‎ 因为，所以.‎ ‎20. （12分）解：（1）与的夹角为，‎ ‎.‎ ‎.‎ ‎（2）向量与的夹角为钝角，‎ ‎，且不能反向共线，‎ ‎，解得 实数的取值范围是且 .‎ ‎21. （12分）解：（1）由得，，‎ 由正弦定理可得， ‎ 可得：，即：，‎ 由，可得：，‎ 又，‎ 可得：．‎ ‎（2）由已知及正弦定理得即可得 ‎ 即故 的面积．‎ ‎22. （12分）解：（1）因为，由正弦定理得 ‎，即，‎ 则 根据余弦定理得 又因为，所以 ‎（2）因为，所以 则 因为三角形为锐角三角形且，所以 则 所以，‎ 所以 即的取值范围为