- 2021-05-22 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012武汉市中考数学试题及答案
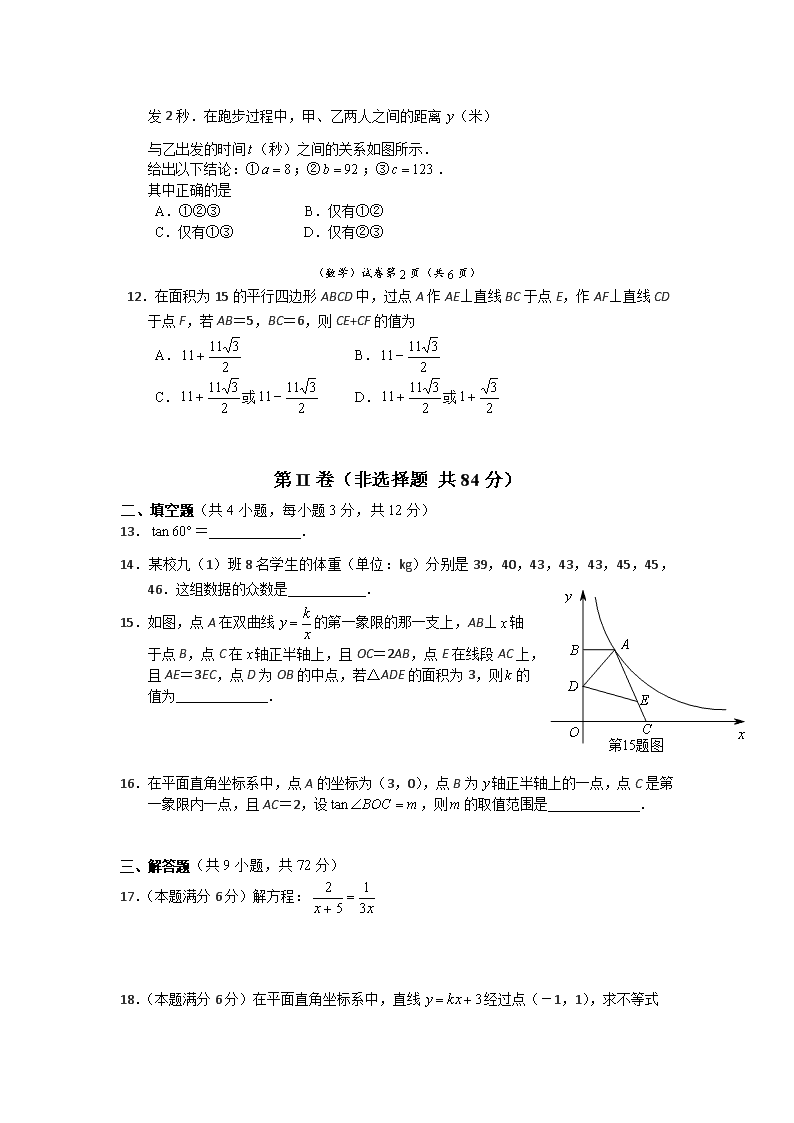
秘密★2012年6月20日 2012年武汉市初中毕业生学业考试 数学试卷 亲爱的同学,在你答题前,请认真阅读下面以及“答题卡”上的注意事项: 1. 本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成。全卷共6页,三大题,满分120分。考试用时120分钟。 2. 答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号。 3. 答第Ⅰ卷(选择题)时,选出每小题答案后,用2B铅笔把“答题卡”上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案。不得答在“试卷”上。 4. 第Ⅱ卷(非选择题)用0.5毫米黑色笔迹签字笔书写在“答题卡”上。答在“试卷”上无效。 预祝你取得优异成绩! 第I卷(选择题 共36分) 一、选择题(共12小题,每小题3分,共36分) 下列各项中均有四个备选答案,其中有且只有一个正确,请在答题卡上将正确答案的代号涂黑. 1.在2.5,-2.5,0,3这四个数中,最小的一个数是 A.2.5 B.-2.5 C.0 D.3 2.式子在实数范围内有意义,则x的取值范围是 A.<3 B.≤3 C.<3 D.≥3 3.在数轴上表示不等式的解集,正确的是 A. B. C. D. 4.从标号分别为1,2,3,4,5的5张卡片中,随机抽出1张,下列事件中,必然事件是 A.标号小于6. B.标号大于6. C.标号是奇数. D.标号是3. 5.若,是一元二次方程的两个根,则的值是 A.-2 B.2 C.3 D.1 (数学)试卷第1页(共6页) 6.某市2012年在校初中生的人数约为23万.数230 000用科学记数法表示为 A. B. C. D. 7.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处.若AE=5,BF=3,则CD的长是 A.7 B.8 C.9 D.10 8.如图,是由4个相同小正方体组合而成的几何体, 它的左视图是 A. B. C. D. 9.一列数,,,…,其中,(为不小于2的整数),则的值为 A. B. C. D. 10.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分共4个等级.将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是 A.2.25 B.2.5 C.2.95 D.3 11.甲、乙两人在直线跑道上同起点、同终点、同方向 匀速跑步500米,先到终点的人原地休息.已知甲先出 发2秒.在跑步过程中,甲、乙两人之间的距离(米) 与乙出发的时间(秒)之间的关系如图所示. 给出以下结论:①;②;③. 其中正确的是 A.①②③ B.仅有①② C.仅有①③ D.仅有②③ (数学)试卷第2页(共6页) 12.在面积为15的平行四边形ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=5,BC=6,则CE+CF的值为 A. B. C.或 D.或 第II卷(非选择题 共84分) 二、填空题(共4小题,每小题3分,共12分) 13.= . 14.某校九(1)班8名学生的体重(单位:kg)分别是39,40,43,43,43,45,45,46.这组数据的众数是 . 15.如图,点A在双曲线的第一象限的那一支上,AB⊥轴 于点B,点C在轴正半轴上,且OC=2AB,点E在线段AC上, 且AE=3EC,点D为OB的中点,若△ADE的面积为3,则的 值为 . 16.在平面直角坐标系中,点A的坐标为(3,0),点B为轴正半轴上的一点,点C是第一象限内一点,且AC=2,设,则的取值范围是 . 三、解答题(共9小题,共72分) 17.(本题满分6分)解方程: 18.(本题满分6分)在平面直角坐标系中,直线经过点(-1,1),求不等式 <0的解集. 19.(本题满分6分)如图,CE=CB,CD=CA, ∠DCA=∠ECB.求证:DE=AB. (数学)试卷第3页(共6页) 20.(本题满分7分)一个口袋中有4个相同的小球,分别写有字母A,B,C,D,随机地摸出一个小球然后放回,再随机地摸出一个小球. (1)试用列表法或树形图中的一种,列举出两次摸出的球上字母的所有可能结果; (2)求两次摸出的球上字母相同的概率. 21.(本题满分7分)如图,在平面直角坐标系中, 点A,B的坐标分别为(-1,3),(-4, 1), 先将线段AB沿一确定方向平移得到线段, 点A的对应点为,点的坐标为(0,2), 再将线段绕原点O顺时针旋转90°得到 线段,点的对应点为. (1)画出线段,; (2)直接写出在这两次变换过程中,点A经过 到达的路径长. 22.(本题满分8分)在锐角△ABC中,BC=5,. (1)如图1,求△ABC的外接圆的直径; (2)如图2,点I为△ABC的内心,若BA=BC,求AI的长. (数学)试卷第4页(共6页) 23.(本题满分10分)如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在直线为轴,抛物线的对称轴为轴建立平面直角坐标系. (1)求抛物线的解析式; (2)已知从某时刻开始40小时内,水面与河底ED的距离(单位:米)随时间(单位:时)的变化满足函数关系 (0≤≤40) 且当水面到顶点C的距离不大于5米时,需禁止船只通行.请通过计算说明:在这一时段内,需多少时禁止船只通行? 24.(本题满分10分)已知△ABC中,. (1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长; (2)如图2,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形. ①请你在所给的网格中画出格点,使得与 △ABC全等(画出一个即可,不需证明); ②试直接写出在所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明). (数学)试卷第5页(共6页) 25.(本题满分12分)如图1,点A为抛物线的顶点,点B的坐标为(1,0),直线AB交抛物线于另一点C. (1)求点C的坐标; (2)如图1,平行于轴的直线交直线AB于点D,交抛物线于点E,平行于轴的直线交直线AB于F,交抛物线于G,若,求的值; (3)如图2,将抛物线向下平移(>0)个单位得到抛物线,且抛物线的顶点为P,交轴负半轴于点M,交射线BC于点N.NQ⊥轴于点Q,当NP平分∠MNQ时,求的值. (数学)试卷第6页(共6页) 答案参考:http://wh.zhongkao.com/e/20120621/4fe1fed68299e.shtml查看更多