- 2021-05-22 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海中考与圆有关的综合题
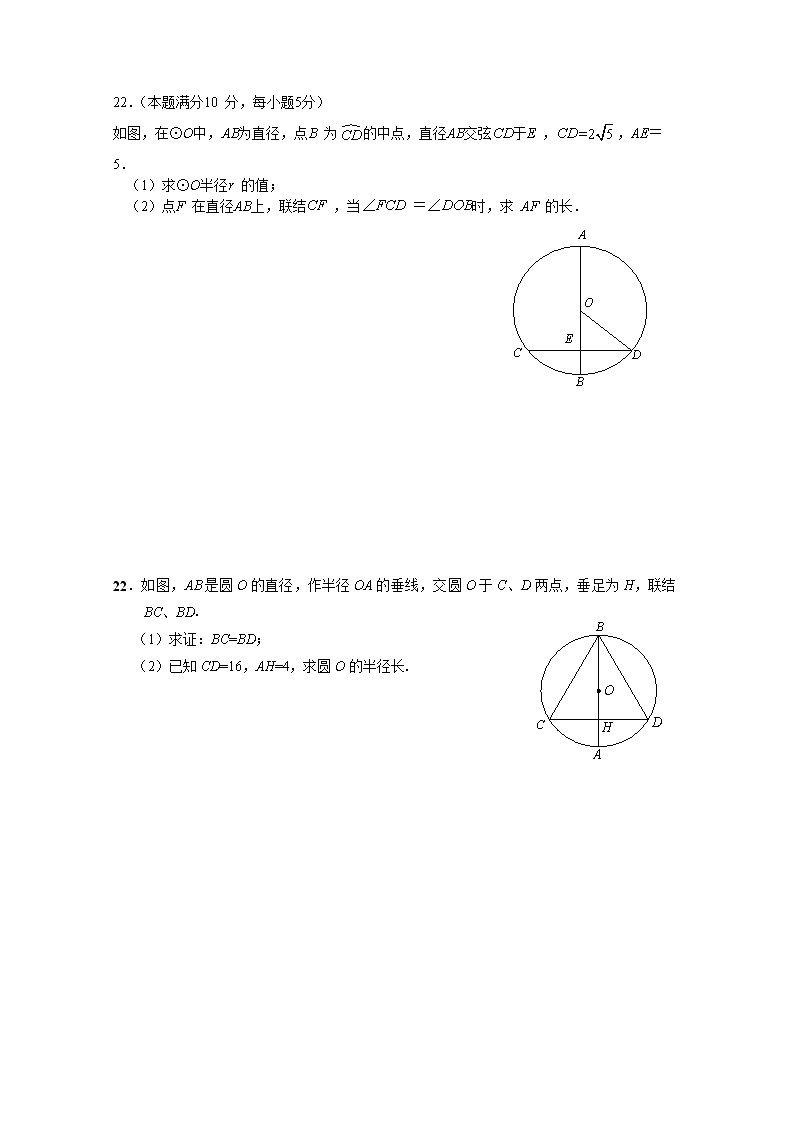
与圆有关的综合题 20.如图,AB、CD是⊙O的两条弦,BA、DC的延长线交于点P ,BPODPO. 求证:PA=PC. 21. 已知,如图,在⊙O中,弦垂直于直径,垂足为点,如果,且 ,求弦的长. 22.(本题满分10 分,每小题5分) 如图,在⊙O中,AB为直径,点B 为的中点,直径AB交弦CD于E ,CD,AE=5. (1)求⊙O半径r 的值; (2)点F 在直径AB上,联结CF ,当∠FCD =∠DOB时,求 AF 的长. 22.如图,AB是圆O的直径,作半径OA的垂线,交圆O于C、D两点,垂足为H,联结BC、BD. (1)求证:BC=BD; (2)已知CD=16,AH=4,求圆O的半径长. 25. 如图,已知在梯形ABCD中,AD // BC,AB ⊥BC,AB = 4,AD = 3,, P是边CD上一点(点P与点C、D不重合),以PC为半径的⊙P与边BC相交于点C和点Q. (1)如果BP⊥CD,求CP的长; (2)联结PQ,如果△ADP和△BQP相似,求CP的长. 图1 备用图 25. 如图,在Rt△ABC中,∠ACB = 90°,AB=5,BC=4,点M是边BC上的动点(与点B、C不重合),以MB长为半径的⊙M与边AB交于点N,联结CN、MN,设MB=,AN=. (1)求与之间的函数解析式,并写出定义域; (2)当∠NMB=∠ANC时,求△CNM与△CBN的周长比; (3)当△CNM是以MN为腰的等腰三角形时,求的值. 25.(本题满分14分,第(1)题3分,第(2)题5分,第(3)题6分) 如图,已知在△ABC中,AB=AC=5,cosB=,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD. (1)求△ABC的面积; (2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域; (3)如果△APD是直角三角形,求PB的长. A B C A P B D C 25.如图,线段AB=4,25.如图,已知△ABC中,AB=AC=,BC=4,点O在BC边上运动,以O为圆心,OA为半径的圆与边AB交于点D(点A除外),设OB,AD . (1)求的值; (2)求关于的函数解析式,并写出函数的定义域; C O D B A (3)当点O在BC边上运动时,⊙O是否可能与以C为圆心,BC长为半径的⊙C相切?如果可能,请求出两圆相切时的值;如果不可能,请说明理由. 25.如图,已知:在△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与B点重合),过点D作射线DE交AB边于点E,使∠BDE=∠A,以D为圆心,DC的长为半径为⊙D (1)设BD=x,AE=y,求y关于x的函数关系,并写出定义域 (2)当⊙D与AB边相切时,求BD的长 (3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD为多少时,⊙D与⊙E相切? 25.如图,已知AB是⊙O的直径,AB=8, 点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,联结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F. (1)若=,求∠F的度数; (2)设写出与之间的函数解析式,并写出定义域; (3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长. 第25题 25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分) 已知:如图,AB是半圆O的直径,弦CD∥AB,动点P、Q分别在线段OC、CD上,且DQ=OP,AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合),AB=20,cos∠AOC=.设OP=x,△CPF的面积为y. (1) 求证:AP=OQ; (2) 求y关于x的函数关系式,并写出它的定义域; (3) 当△OPE是直角三角形时,求线段OP的长. 备用图 25.(本题满分14分,其中第(1)、(2)小题各4分、第(3)小题6分) 已知:如图,在边长为5的菱形ABCD中,cosA=,点P为边AB上一点,以A为圆心、AP为半径的⊙A与边AD交于点E,射线CE 与⊙A另一个交点为点F. (1)当点E与点D重合时,求EF的长; (2)设AP=x,CE=y,求y关于x的函数关系式及定义域; D C B A E F P D C B A 备用图 (3)是否存在一点P,使得弧EF的长是弧PE的2倍,若存在,求AP的长,若不存在,请说明理由. 24.如图,已知二次函数的图象经过三点,,且与y轴交于点C. (1)求这个二次函数的解析式,并写出顶点M及点C的坐标; (2)若直线经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形; (3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切,如果存在,请求出点P的坐标;如果不存在,请说明理由. 25.如图,已知在△ABC中,AB=15,AC=20,,P是边AB上的一个动点,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与边AC相切;当点P与点B不重合,且⊙P与边AC相交于点M和点N时,设AP=x,MN=y. (1)求⊙P的半径; (2)求y关于x的函数解析式,并写出它的定义域; A B P M N C (3)当AP=时,试比较∠CPN与∠A的大小,并说明理由. 25.在矩形ABCD中,点是边AD上的动点,联结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,联结QP(图10).已知AD13,AB5,设AP=x ,BQ = y. (1)求关于的函数解析式,并写出的取值范围; (2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,求的值; (3)点E在边CD上,过点作直线QP的垂线,垂足为F,如果EFEC4,求的值. 备用图beibeiyongtu 25.(本题满分14分,第(1)小题满分3分,第(1)小题满分5分,第(1)小题满分6分)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G. (1)当圆C经过点A时,求CP的长; (2)联结AP,当AP//CG时,求弦EF的长; (3)当△AGE是等腰三角形时,求圆C的半径长. 图1 备用图 24.如图,已知⊙C的圆心在x轴上,且经过、两点,抛物线 (m>0)经过A、B两点,顶点为P. (1)求抛物线与y轴的交点D的坐标(用m的代数式表示); C. A B D P O x y 第24题 (2)当m为何值时,直线PD与圆C相切? 25.(本题满分14分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分6分) 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E. (1)当BC=1时,求线段OD的长; (2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由; (3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域. 25.如图1,在半径为5的扇形AOB中,,点C、D分别在半径OA与弧AB上,且,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF. (1)求的值; (2)如图2,联结EO、FO,若,求CP的长; (3)设,△DEF的面积为y,求y关于x的函数解析式,并写出定义域. 25、(本题满分14分,其中第(1)小题5分,第(2)小题5分,第(3)小题4分) 已知:⊙O的半径为3,弦,垂足为,点E在⊙O上,,射线 CE与射线相交于点.设 . (1)求与之间的函数解析式,并写出函数定义域; (2)当为直角三角形时,求的长; (3)如果,求的长. (第25题图) O E F B C D A (备用图1) O 25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题每小题5分,) 已知:如图,A、B是⊙O上两点,OA = 5,AB = 8,C是上任意一点,OC与弦AB相交于点D,过点C作CE⊥OB,交射线BO于点E,CE的延长线交⊙O于点F,联结BC、BF、OF. (1)如图1,当点E是线段BO的中点时,求弦BF的长; (2)当点E在线段BO上时,设AD = x,,求y关于x的函数解析式,并写出这个函数的定义域; (3)当CD = 1时,求四边形OCBF的面积. A B O C E D F (第25题图) A B O (备用图) A B C O D E F (图1) 25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 如图,已知线段AB=10,点C在线段AB上,⊙A、⊙B的半径分别为AC、BC,D是⊙B上一点,AD交⊙A于E,EC的延长线交⊙B于F. (1) 求证:BF//AD; (2) 若BD⊥AD,AC=,DF=,求与的函数关系式,写出定义域. (3)在(2)的条件下,点C在线段AB上运动的过程中,DF是否有可能与AB垂直,如果有可能请求出AC的长,如果没有可能,请说明理由. (第25题) 25.如图,已知在中,,,,点是边上的一点,,垂足为,以点为圆心,为半径的圆与射线相交于点,线段与边交于点。 (1) 求的长; (2) 设,的面积为,求关于的函数解析式,并写出定义域; (3) 过点作,垂足为,联结、,如果是以为腰的等腰三角形,求的长。 25.(本题共3小题,其中第(1)小题各4分,第(2)、(3)小题各5分,满分14分) 如图,在梯形ABCD中,AD // BC,∠B = 90°,AB = 4,BC = 9,AD = 6.点E、F分别在边AD、BC上,且BF = 2DE,联结FE.FE的延长线与CD的延长线相交于点P.设 DE = x,. (1)求y关于x的函数解析式,并写出函数的定义域; (2)当以ED为半径的⊙E与以FB为半径的⊙F外切时,求x的值; (3)当△AEF∽△PED时,求x的值. A B C D E F P A B C D (备用图) 25.以AB为直径作半圆O,点C为弧AB的中点,点P为直径AB上一点,联结PC,过点C作CD//AB,且CD=PC,过点D作DE//PC,交射线PB于点E,PD与CE相交于点Q. (1)若点P与点A重合,求BE的长; (2)设PC= x,,当点P在线段AO上时,求y与x的函数关系式及定义域; (3)当点Q在半圆O上时,求PC的长. A C P O B D E Q 备用图 A O B C查看更多