- 2021-05-22 发布 |
- 37.5 KB |
- 25页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年四川省乐山市中考数学试卷(含解析)
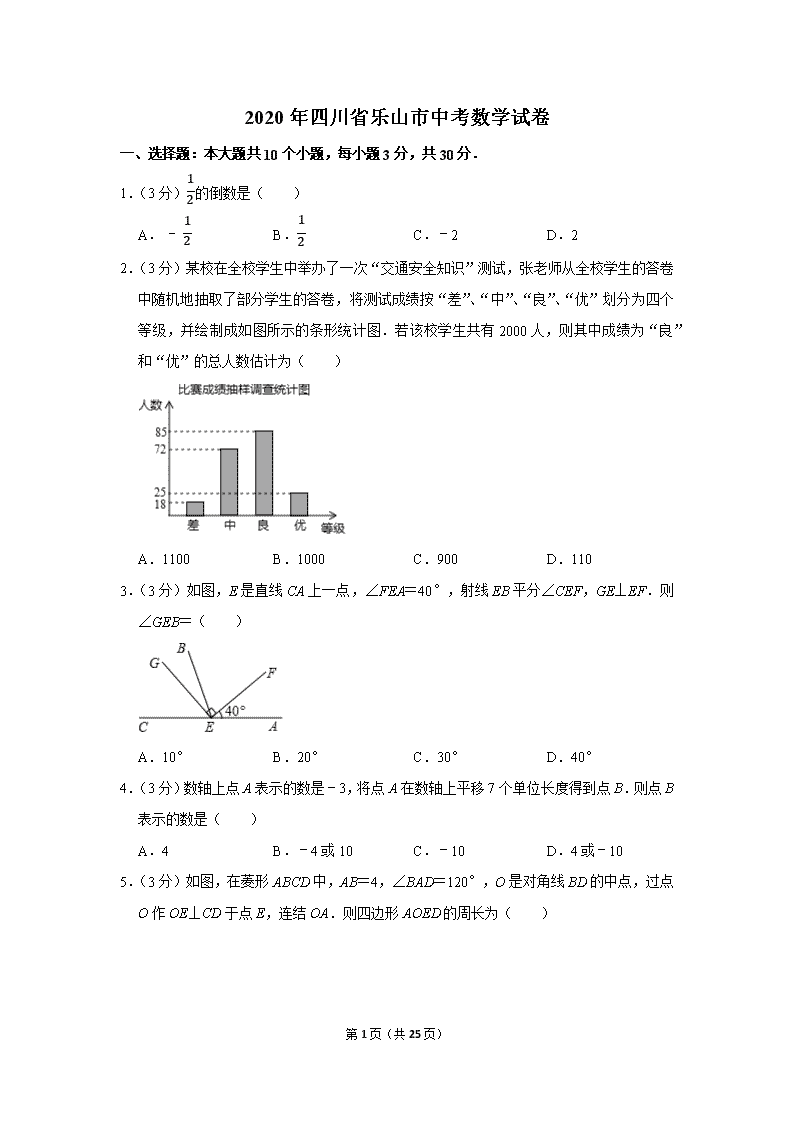
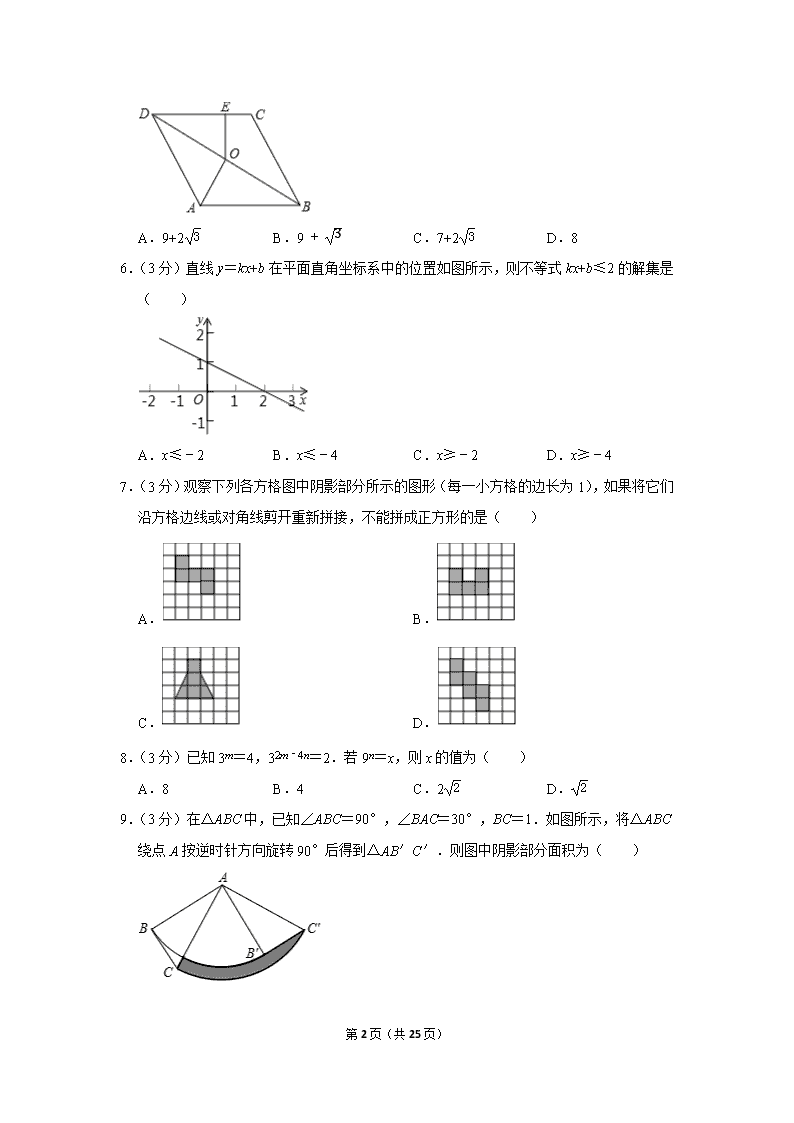
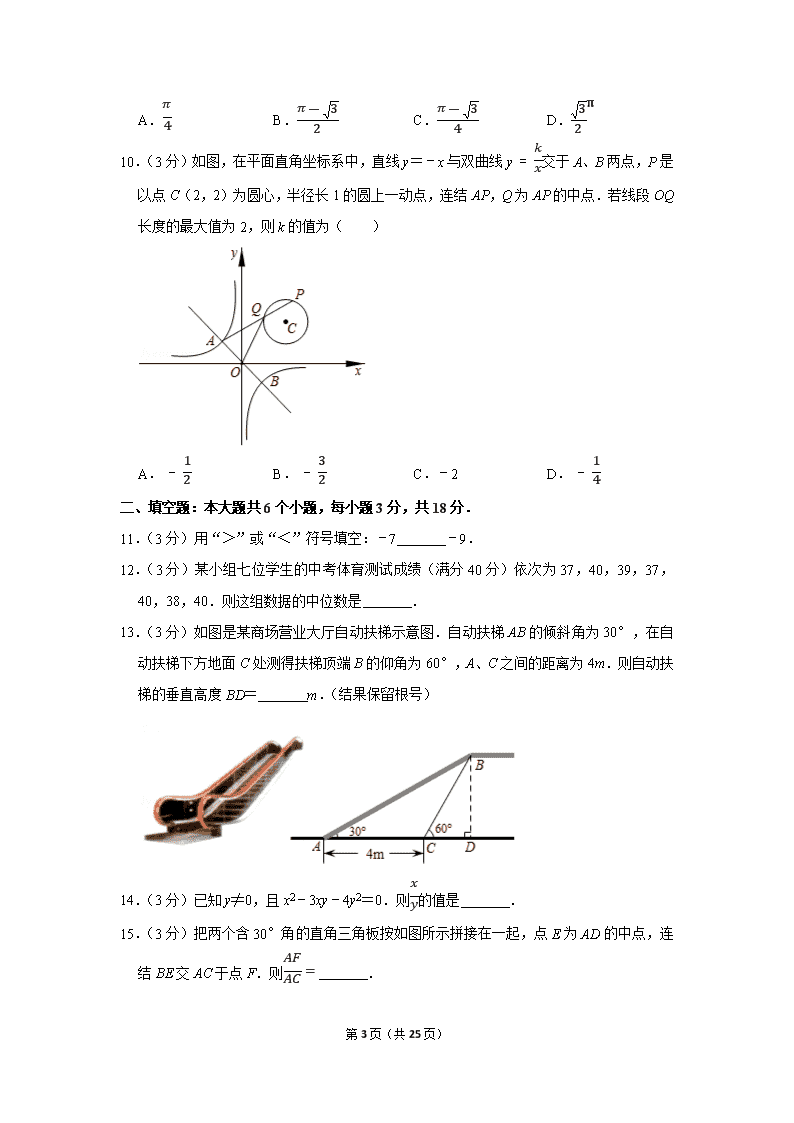
2020年四川省乐山市中考数学试卷 一、选择题:本大题共10个小题,每小题3分,共30分. 1.(3分)12的倒数是( ) A.-12 B.12 C.﹣2 D.2 2.(3分)某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( ) A.1100 B.1000 C.900 D.110 3.(3分)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( ) A.10° B.20° C.30° D.40° 4.(3分)数轴上点A表示的数是﹣3,将点A在数轴上平移7个单位长度得到点B.则点B表示的数是( ) A.4 B.﹣4或10 C.﹣10 D.4或﹣10 5.(3分)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连结OA.则四边形AOED的周长为( ) 第25页(共25页) A.9+23 B.9+3 C.7+23 D.8 6.(3分)直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤2的解集是( ) A.x≤﹣2 B.x≤﹣4 C.x≥﹣2 D.x≥﹣4 7.(3分)观察下列各方格图中阴影部分所示的图形(每一小方格的边长为1),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是( ) A. B. C. D. 8.(3分)已知3m=4,32m﹣4n=2.若9n=x,则x的值为( ) A.8 B.4 C.22 D.2 9.(3分)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( ) 第25页(共25页) A.π4 B.π-32 C.π-34 D.32π 10.(3分)如图,在平面直角坐标系中,直线y=﹣x与双曲线y=kx交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连结AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( ) A.-12 B.-32 C.﹣2 D.-14 二、填空题:本大题共6个小题,每小题3分,共18分. 11.(3分)用“>”或“<”符号填空:﹣7 ﹣9. 12.(3分)某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的中位数是 . 13.(3分)如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为4m.则自动扶梯的垂直高度BD= m.(结果保留根号) 14.(3分)已知y≠0,且x2﹣3xy﹣4y2=0.则xy的值是 . 15.(3分)把两个含30°角的直角三角板按如图所示拼接在一起,点E为AD的中点,连结BE交AC于点F.则AFAC= . 第25页(共25页) 16.(3分)我们用符号[x]表示不大于x的最大整数.例如:[1.5]=1,[﹣1.5]=﹣2.那么: (1)当﹣1<[x]≤2时,x的取值范围是 ; (2)当﹣1≤x<2时,函数y=x2﹣2a[x]+3的图象始终在函数y=[x]+3的图象下方.则实数a的范围是 . 三、本大题共3个小题,每小题9分,共27分. 17.(9分)计算:|﹣2|﹣2cos60°+(π﹣2020)0. 18.(9分)解二元一次方程组:2x+y=2,8x+3y=9. 19.(9分)如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度. 四、本大题共3个小题,每小题10分,共30分. 20.(10分)已知y=2x,且x≠y,求(1x-y+1x+y)÷x2yx2-y2的值. 21.(10分)如图,已知点A(﹣2,﹣2)在双曲线y=kx上,过点A的直线与双曲线的另一支交于点B(1,a). (1)求直线AB的解析式; (2)过点B作BC⊥x轴于点C,连结AC,过点C作CD⊥AB于点D.求线段CD的长. 第25页(共25页) 22.(10分)自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图. 根据上面图表信息,回答下列问题: (1)截止5月31日该国新冠肺炎感染总人数累计为 万人,扇形统计图中40﹣59岁感染人数对应圆心角的度数为 °; (2)请直接在图中补充完整该国新冠肺炎感染人数的折线统计图; (3)在该国所有新冠肺炎感染病例中随机地抽取1人,求该患者年龄为60岁或60岁以上的概率; (4)若该国感染病例中从低到高各年龄段的死亡率依次为1%、2.75%、3.5%、10%、20%,求该国新冠肺炎感染病例的平均死亡率. 五、本大题共2个小题,每小题10分,共20分. 23.(10分)某汽车运输公司为了满足市场需要,推出商务车和轿车对外租赁业务.下面是乐山到成都两种车型的限载人数和单程租赁价格表: 第25页(共25页) 车型 每车限载人数(人) 租金(元/辆) 商务车 6 300 轿车 4 (1)如果单程租赁2辆商务车和3辆轿车共需付租金1320元,求一辆轿车的单程租金为多少元? (2)某公司准备组织34名职工从乐山赴成都参加业务培训,拟单程租用商务车或轿车前往.在不超载的情况下,怎样设计租车方案才能使所付租金最少? 24.(10分)如图1,AB是半圆O的直径,AC是一条弦,D是AC上一点,DE⊥AB于点E,交AC于点F,连结BD交AC于点G,且AF=FG. (1)求证:点D平分AC; (2)如图2所示,延长BA至点H,使AH=AO,连结DH.若点E是线段AO的中点.求证:DH是⊙O的切线. 六、本大题共2个小题,第25题12分,第26题13分,共25分. 25.(12分)点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F.点O为AC的中点. (1)如图1,当点P与点O重合时,线段OE和OF的关系是 ; (2)当点P运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立? (3)如图3,点P在线段OA的延长线上运动,当∠OEF=30°时,试探究线段CF、AE、OE之间的关系. 第25页(共25页) 26.(13分)已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连结BC,且tan∠CBD=43,如图所示. (1)求抛物线的解析式; (2)设P是抛物线的对称轴上的一个动点. ①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连结FB、FC,求△BCF的面积的最大值; ②连结PB,求35PC+PB的最小值. 第25页(共25页) 2020年四川省乐山市中考数学试卷 参考答案与试题解析 一、选择题:本大题共10个小题,每小题3分,共30分. 1.(3分)12的倒数是( ) A.-12 B.12 C.﹣2 D.2 【解答】解:根据倒数的定义,可知12的倒数是2. 故选:D. 2.(3分)某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( ) A.1100 B.1000 C.900 D.110 【解答】解:2000×85+2525+85+72+18=1100(人), 故选:A. 3.(3分)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( ) A.10° B.20° C.30° D.40° 【解答】解:∵∠FEA=40°,GE⊥EF, ∴∠CEF=180°﹣∠FEA=180°﹣40°=140°,∠CEG=180°﹣∠AEF﹣∠GEF= 第25页(共25页) 180°﹣40°﹣90°=50°, ∵射线EB平分∠CEF, ∴∠CEB=12∠CEF=12×140°=70°, ∴∠GEB=∠CEB﹣∠CEG=70°﹣50°=20°, 故选:B. 4.(3分)数轴上点A表示的数是﹣3,将点A在数轴上平移7个单位长度得到点B.则点B表示的数是( ) A.4 B.﹣4或10 C.﹣10 D.4或﹣10 【解答】解:点A表示的数是﹣3,左移7个单位,得﹣3﹣7=﹣10, 点A表示的数是﹣3,右移7个单位,得﹣3+7=4. 所以点B表示的数是4或﹣10. 故选:D. 5.(3分)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连结OA.则四边形AOED的周长为( ) A.9+23 B.9+3 C.7+23 D.8 【解答】解:∵四边形ABCD为菱形, ∴AD=AB=4,AB∥CD, ∵∠BAD=120°, ∴∠ADB=∠CDB=30°, ∵O是对角线BD的中点, ∴AO⊥BD, 在Rt△AOD中,AO=12AD=2, OD=3OA=23, ∵OE⊥CD, ∴∠DEO=90°, 第25页(共25页) 在Rt△DOE中,OE=12OD=3, DE=3OE=3, ∴四边形AOED的周长=4+2+3+3=9+3. 故选:B. 6.(3分)直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤2的解集是( ) A.x≤﹣2 B.x≤﹣4 C.x≥﹣2 D.x≥﹣4 【解答】解:∵直线y=kx+b与x轴交于点(2,0),与y轴交于点(0,1), ∴2k+b=0b=1,解得k=-12b=1 ∴直线为y=-12x+1, 当y=2时,2=-12x+1,解得x=﹣2, 由图象可知:不等式kx+b≤2的解集是x≥﹣2, 故选:C. 7.(3分)观察下列各方格图中阴影部分所示的图形(每一小方格的边长为1),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是( ) A. B. C. D. 【解答】解:由题意,选项D阴影部分面积为6,A,B,C的阴影部分的面积为5, 如果能拼成正方形,选项D的正方形的边长为6,选项A,B,C的正方形的边长为5, 第25页(共25页) 观察图象可知,选项A,B,C阴影部分沿方格边线或对角线剪开均可得图1的5个图形,可以拼成图2的边长为5的正方形, 故选:D. 8.(3分)已知3m=4,32m﹣4n=2.若9n=x,则x的值为( ) A.8 B.4 C.22 D.2 【解答】解:∵3m=4,32m﹣4n=(3m)2÷(3n)4=2. ∴42÷(3n)4=2, ∴(3n)4=42÷2=8, 又∵9n=32n=x, ∴(3n)4=(32n)2=x2, ∴x2=8, ∴x=8=22. 故选:C. 9.(3分)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( ) A.π4 B.π-32 C.π-34 D.32π 【解答】解:∵∠ABC=90°,∠BAC=30°,BC=1, ∴AB=3BC=3,AC=2BC=2, ∴90⋅π×22360-90⋅π×3360-(12×1×3-30⋅π×3360)=π-32, 故选:B. 第25页(共25页) 10.(3分)如图,在平面直角坐标系中,直线y=﹣x与双曲线y=kx交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连结AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( ) A.-12 B.-32 C.﹣2 D.-14 【解答】解:点O是AB的中点,则OQ是△ABP的中位线, 当B、C、P三点共线时,PB最大,则OQ=12BP最大, 而OQ的最大值为2,故BP的最大值为4, 则BC=BP﹣PC=4﹣1=3, 设点B(m,﹣m),则(m﹣2)2+(﹣m﹣2)2=32, 解得:m2=12, ∴k=m(﹣m)=-12, 故选:A. 二、填空题:本大题共6个小题,每小题3分,共18分. 11.(3分)用“>”或“<”符号填空:﹣7 > ﹣9. 【解答】解:∵|﹣7|=7,|﹣9|=9,7<9, ∴﹣7>﹣9, 故答案为:>. 12.(3分)某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的中位数是 39 . 【解答】解:把这组数据从小到大排序后为37,37,38,39,40,40,40, 其中第四个数据为39, 第25页(共25页) 所以这组数据的中位数为39. 故答案为39. 13.(3分)如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为4m.则自动扶梯的垂直高度BD= 23 m.(结果保留根号) 【解答】解:∵∠BCD=∠BAC+∠ABC,∠BAC=30°,∠BCD=60°, ∴∠ABC=∠BCD﹣∠BAC=30°, ∴∠BAC=∠ABC, ∴BC=AC=4, 在Rt△BDC中,sin∠BCD=BDBC, ∴sin60°=BD4=32, ∴BD=23(m), 答:自动扶梯的垂直高度BD=23m, 故答案为:23. 14.(3分)已知y≠0,且x2﹣3xy﹣4y2=0.则xy的值是 4或﹣1 . 【解答】解:∵x2﹣3xy﹣4y2=0,即(x﹣4y)(x+y)=0, 可得x=4y或x=﹣y, ∴xy=4或xy=-1, 即xy的值是4或﹣1; 故答案为:4或﹣1. 15.(3分)把两个含30°角的直角三角板按如图所示拼接在一起,点E为AD的中点,连结BE交AC于点F.则AFAC= 35 . 第25页(共25页) 【解答】解:连接CE,∵∠CAD=30°,∠ACD=90°,E是AD的中点, ∴AC=32AD,CE=12AD=AE, ∴∠ACE=∠CAE=30° ∵∠BAC=30°,∠ABC=90°, ∴AB=32AC=34AD,∠BAC=∠ACE, ∴AB∥CE, ∴△ABF∽△CEF, ∴AFCF=ABCE=34AD12AD=32, ∴AFAC=35, 故答案为35. 16.(3分)我们用符号[x]表示不大于x的最大整数.例如:[1.5]=1,[﹣1.5]=﹣2.那么: (1)当﹣1<[x]≤2时,x的取值范围是 0≤x≤2 ; (2)当﹣1≤x<2时,函数y=x2﹣2a[x]+3的图象始终在函数y=[x]+3的图象下方.则实数a的范围是 a<-1或a≥32 . 【解答】解:(1)由题意∵﹣1<[x]≤2, ∴0≤x≤2, 故答案为0≤x≤2. (2)由题意:当﹣1≤x<2时,函数y=x2﹣2a[x]+3的图象始终在函数y=[x]+3的图象 第25页(共25页) 下方, 则有x=﹣1时,1+2a+3<﹣1+3,解得a<﹣1, 或x=2时,4﹣2a+3≤1+3,解得a≥32, 故答案为a<﹣1或a≥32. 三、本大题共3个小题,每小题9分,共27分. 17.(9分)计算:|﹣2|﹣2cos60°+(π﹣2020)0. 【解答】解:原式=2-2×12+1 =2. 18.(9分)解二元一次方程组:2x+y=2,8x+3y=9. 【解答】解:2x+y=2①8x+3y=9②, 法1:②﹣①×3,得 2x=3, 解得:x=32, 把x=32代入①,得 y=﹣1, ∴原方程组的解为x=32y=-1; 法2:由②得:2x+3(2x+y)=9, 把①代入上式, 解得:x=32, 把x=32代入①,得 y=﹣1, ∴原方程组的解为x=32y=-1. 19.(9分)如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度. 第25页(共25页) 【解答】解:∵四边形ABCD是矩形, ∴DC=AB=3,∠ADC=∠C=90°. ∵CE=1, ∴DE=DC2+CE2=10. ∵AF⊥DE, ∴∠AFD=90°=∠C,∠∠ADF+∠DAF=90°. 又∵∠ADF+∠EDC=90°, ∴∠EDC=∠DAF, ∴△EDC∽△DAF, ∴DEAD=CEFD,即102=1FD, ∴FD=105,即DF的长度为105. 四、本大题共3个小题,每小题10分,共30分. 20.(10分)已知y=2x,且x≠y,求(1x-y+1x+y)÷x2yx2-y2的值. 【解答】解:原式=2x(x+y)(x-y)÷x2yx2-y2 =2xx2-y2×x2-y2x2y =2xy, ∵y=2x, 第25页(共25页) ∴原式=2x⋅2x=1 解法2:同解法1,得原式=2xy, ∵y=2x, ∴xy=2, ∴原式=22=1. 21.(10分)如图,已知点A(﹣2,﹣2)在双曲线y=kx上,过点A的直线与双曲线的另一支交于点B(1,a). (1)求直线AB的解析式; (2)过点B作BC⊥x轴于点C,连结AC,过点C作CD⊥AB于点D.求线段CD的长. 【解答】解:(1)将点A(﹣2,﹣2)代入y=kx,得k=4, 即y=4x, 将B(1,a)代入y=4x,得a=4, 即B(1,4), 设直线AB的解析式为y=mx+n, 将A(﹣2,﹣2)、B(1,4)代入y=kx+b,得-2=-2m+n4=m+n,解得m=2n=2, ∴直线AB的解析式为y=2x+2; (2)∵A(﹣2,﹣2)、B(1,4), 第25页(共25页) ∴AB=(-2-1)2+(-2-4)2=35, ∵S△ABC=12×AB×CD=12×BC×3, ∴CD=BC×3AB=4×335=455. 22.(10分)自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图. 根据上面图表信息,回答下列问题: (1)截止5月31日该国新冠肺炎感染总人数累计为 20 万人,扇形统计图中40﹣59岁感染人数对应圆心角的度数为 72 °; (2)请直接在图中补充完整该国新冠肺炎感染人数的折线统计图; (3)在该国所有新冠肺炎感染病例中随机地抽取1人,求该患者年龄为60岁或60岁以上的概率; (4)若该国感染病例中从低到高各年龄段的死亡率依次为1%、2.75%、3.5%、10%、20%,求该国新冠肺炎感染病例的平均死亡率. 【解答】解:(1)截止5月31日该国新冠肺炎感染总人数累计为9÷45%=20(万人), 扇形统计图中40﹣59岁感染人数对应圆心角的度数为360°×420=72°, 故答案为:20、72; (2)20﹣39岁人数为20×10%=2(万人), 补全的折线统计图如图2所示; 第25页(共25页) (3)该患者年龄为60岁及以上的概率为:9+4.520×100%=67.5%=0.675; (4)该国新冠肺炎感染病例的平均死亡率为:0.5×1%+2×2.75%+4×3.5%+9×10%+4.5×20%20×100%=10%. 五、本大题共2个小题,每小题10分,共20分. 23.(10分)某汽车运输公司为了满足市场需要,推出商务车和轿车对外租赁业务.下面是乐山到成都两种车型的限载人数和单程租赁价格表: 车型 每车限载人数(人) 租金(元/辆) 商务车 6 300 轿车 4 (1)如果单程租赁2辆商务车和3辆轿车共需付租金1320元,求一辆轿车的单程租金为多少元? (2)某公司准备组织34名职工从乐山赴成都参加业务培训,拟单程租用商务车或轿车前往.在不超载的情况下,怎样设计租车方案才能使所付租金最少? 【解答】解:(1)设租用一辆轿车的租金为x元, 由题意得:300×2+3x=1320, 解得 x=240, 答:租用一辆轿车的租金为240元; 第25页(共25页) (2)①若只租用商务车, ∵346=523, ∴只租用商务车应租6辆,所付租金为300×6=1800(元); ②若只租用轿车, ∵344=8.5, ∴只租用轿车应租9辆,所付租金为240×9=2160(元); ③若混和租用两种车,设租用商务车m辆,租用轿车n辆,租金为W元. 由题意,得 6m+4n=34W=300m+240n, 由6m+4n=34,得 4n=﹣6m+34, ∴W=300m+60(﹣6m+34)=﹣60m+2040, ∵﹣6m+34=4n≥0, ∴m≤173, ∴1≤m≤5,且m为整数, ∵W随m的增大而减小, ∴当m=5时,W有最小值1740,此时n=1. 综上,租用商务车5辆和轿车1辆时,所付租金最少为1740元. 24.(10分)如图1,AB是半圆O的直径,AC是一条弦,D是AC上一点,DE⊥AB于点E,交AC于点F,连结BD交AC于点G,且AF=FG. (1)求证:点D平分AC; (2)如图2所示,延长BA至点H,使AH=AO,连结DH.若点E是线段AO的中点.求证:DH是⊙O的切线. 【解答】证明:(1)如图1,连接AD、BC, ∵AB是半圆O的直径, ∴∠ADB=90°, 第25页(共25页) ∵DE⊥AB, ∴∠ADE=∠ABD, 又∵AF=FG,即点F是Rt△AGD的斜边AG的中点, ∴DF=AF, ∴∠DAF=∠ADF=∠ABD, 又∵∠DAC=∠DBC, ∴∠ABD=∠DBC, ∴AD=DC, ∴即点D平分AC; (2)如图2所示,连接OD、AD, ∵点E是线段OA的中点, ∴OE=12OA=12OD, ∴∠AOD=60°, ∴△OAD是等边三角形, ∴AD=AO=AH, ∴△ODH是直角三角形,且∠HDO=90°, ∴DH是⊙O的切线. 六、本大题共2个小题,第25题12分,第26题13分,共25分. 25.(12分)点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F.点O为AC 第25页(共25页) 的中点. (1)如图1,当点P与点O重合时,线段OE和OF的关系是 OE=OF ; (2)当点P运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立? (3)如图3,点P在线段OA的延长线上运动,当∠OEF=30°时,试探究线段CF、AE、OE之间的关系. 【解答】解:(1)∵四边形ABCD是平行四边形, ∴AO=CO, 又∵∠AEO=∠CFO,∠AOE=∠COF=90°, ∴△AEO≌△CFO(AAS), ∴OE=OF, 故答案为:OE=OF; (2)补全图形如图所示, 结论仍然成立, 理由如下: 延长EO交CF于点G, ∵AE⊥BP,CF⊥BP, ∴AE∥CF, ∴∠EAO=∠GCO, ∵点O为AC的中点, 第25页(共25页) ∴AO=CO, 又∵∠AOE=∠COG, ∴△AOE≌△COG(AAS), ∴OE=OG, ∵∠GFE=90°, ∴OE=OF; (4)点P在线段OA的延长线上运动时,线段CF、AE、OE之间的关系为OE=CF+AE, 证明如下:如图,延长EO交FC的延长线于点H, 由(2)可知△AOE≌△COH, ∴AE=CH,OE=OH, 又∵∠OEF=30°,∠HFE=90°, ∴HF=12EH=OE, ∴OE=CF+CH=CF+AE. 26.(13分)已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连结BC,且tan∠CBD=43,如图所示. (1)求抛物线的解析式; (2)设P是抛物线的对称轴上的一个动点. ①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连结FB、FC,求△BCF的面积的最大值; ②连结PB,求35PC+PB的最小值. 第25页(共25页) 【解答】解:(1)根据题意,可设抛物线的解析式为:y=a(x+1)(x﹣5), ∵抛物线的对称轴为直线x=2, ∴D(2,0), 又∵tan∠CBD=43=CDDB, ∴CD=BD•tan∠CBD=4, 即C(2,4), 代入抛物线的解析式,得4=a(2+1)(2﹣5), 解得 a=-49, ∴二次函数的解析式为 y=-49(x+1)(x-5)=-49x2+169x+209; (2)①设P(2,t),其中0<t<4, 设直线BC的解析式为 y=kx+b, ∴0=5k+b,4=2k+b., 解得 k=-43,b=203. 即直线BC的解析式为 y=-43x+203, 令y=t,得:x=5-34t, ∴点E(5-34t,t), 把x=5-34t 代入y=-49(x+1)(x-5),得 y=t(2-t4), 即F(5-34t,2t-14t2), 第25页(共25页) ∴EF=(2t-14t2)-t=t-t24, ∴△BCF的面积=12×EF×BD=32(t-t24)=-38(t2-4t)=-38(t-2)2+32, ∴当t=2时,△BCF的面积最大,且最大值为32; ②如图,连接AC,根据图形的对称性可知∠ACD=∠BCD,AC=BC=5, ∴sin∠ACD=ADAC=35, 过点P作PG⊥AC于G,则在Rt△PCG中,PG=PC⋅sin∠ACD=35PC, ∴35PC+PB=PG+PB, 过点B作BH⊥AC于点H,则PG+PH≥BH, ∴线段BH的长就是35PC+PB的最小值, ∵S△ABC=12×AB×CD=12×6×4=12, 又∵S△ABC=12×AC×BH=52BH, ∴52BH=12, 即BH=245, ∴35PC+PB的最小值为245. 第25页(共25页)查看更多