上海市各区中考二模数学分类汇编压轴题专题含答案

上海市各区中考二模数学分类汇编压轴题专题含答案

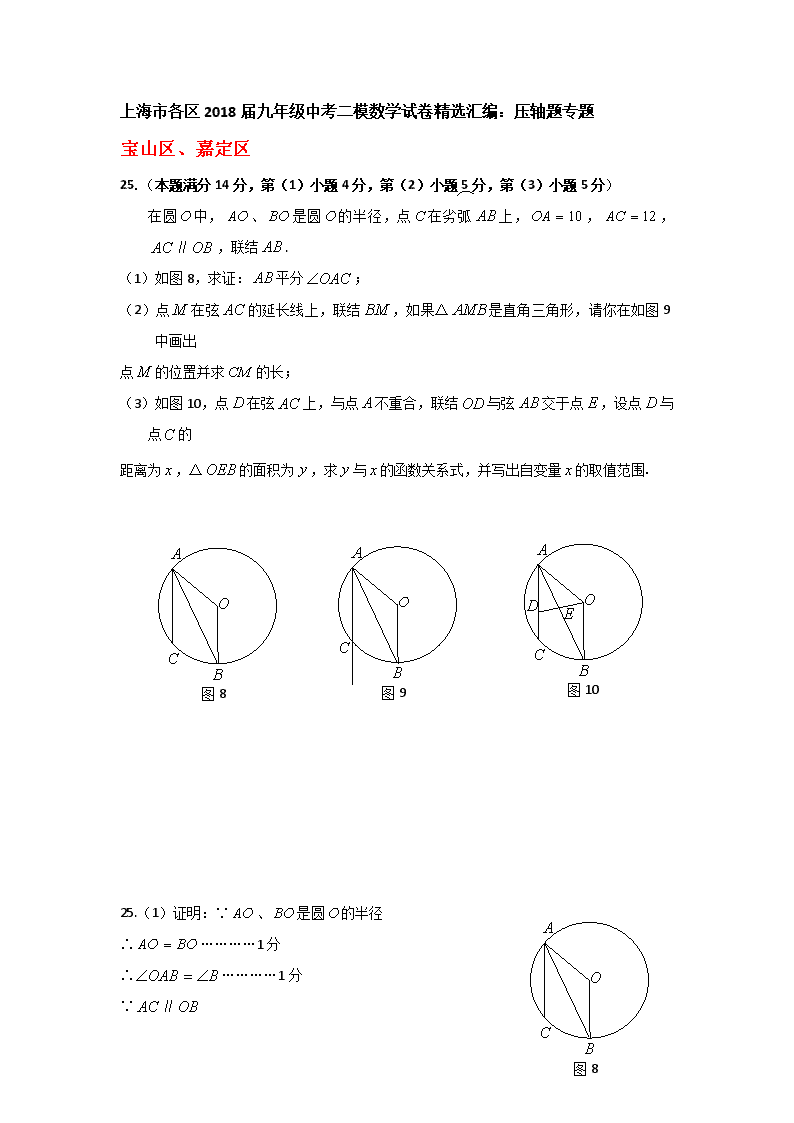
上海市各区2018届九年级中考二模数学试卷精选汇编：压轴题专题 宝山区、嘉定区 ‎25.（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）‎ 在圆中，、是圆的半径，点在劣弧上，，，∥，联结.‎ ‎（1）如图8，求证：平分；‎ ‎（2）点在弦的延长线上，联结，如果△是直角三角形，请你在如图9中画出 点的位置并求的长；‎ ‎（3）如图10，点在弦上，与点不重合，联结与弦交于点，设点与点的 距离为，△的面积为，求与的函数关系式，并写出自变量的取值范围.‎ 图8‎ 图9‎ 图10‎ 图8‎ ‎25.（1）证明：∵、是圆的半径 ‎∴…………1分 ‎∴…………1分 ‎∵∥‎ ‎∴…………1分 ‎∴‎ ‎∴平分…………1分 ‎(2)解：由题意可知不是直角，‎ 所以△是直角三角形只有以下两种情况:‎ 和 ‎ ① 当，点的位置如图9-1……………1分 图9-1‎ 过点作,垂足为点 ‎∵经过圆心 ∴‎ ‎∵ ∴‎ 在Rt△中，‎ ‎∵ ∴‎ ‎∵∥ ∴‎ ‎∵ ∴‎ ‎∴四边形是矩形 图9-2‎ ‎∴‎ ‎∴……………2分 ‎②当，点的位置如图9-2‎ 由①可知，‎ 在Rt△中，‎ ‎∴‎ ‎……………2分 综上所述，的长为或.‎ 说明：只要画出一种情况点的位置就给1分，两个点都画正确也给1分.‎ ‎（3）过点作,垂足为点 图10‎ 由（1）、（2）可知，‎ 由（2）可得： ‎ ‎∵∴……………1分 ‎∵∥∴……………1分 又,,‎ ‎∴ ∴ ……………1分 ‎∴ ‎ ‎∴……………1分 自变量的取值范围为……………1分 长宁区 ‎25．（本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）‎ 在圆O中，C是弦AB上的一点，联结OC并延长，交劣弧AB于点D，联结AO、BO、AD、BD. 已知圆O的半径长为5 ，弦AB的长为8．‎ ‎（1）如图1，当点D是弧AB的中点时，求CD的长；‎ ‎（2）如图2，设AC=x，，求y关于x的函数解析式并写出定义域；‎ ‎（3）若四边形AOBD是梯形，求AD的长． ‎ ‎ ‎ 图1‎ 图2‎ 备用图 第25题图tututu图 ‎25.（本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）‎ 解：（1）∵OD过圆心，点D是弧AB的中点，AB=8，‎ ‎∴OD⊥AB， （2分）‎ 在Rt△AOC中，，AO=5，‎ ‎∴ （1分）‎ ‎， （1分）‎ ‎（2）过点O作OH⊥AB，垂足为点H，则由（1）可得AH=4，OH=3‎ ‎∵AC=x，∴ ‎ 在Rt△HOC中，，AO=5，‎ ‎∴， （1分）‎ ‎∴‎ ‎ （） （3分）‎ ‎（3）①当OB//AD时， 过点A作AE⊥OB交BO延长线于点E，过点O作OF⊥AD,垂足为点F，‎ 则OF=AE， ∴‎ 在Rt△AOF中，，AO=5，‎ ‎∴ ∵OF过圆心，OF⊥AD，∴. （3分）‎ ‎②当OA//BD时， 过点B作BM⊥OA交AO延长线于点M，过点D作DG⊥AO，垂足为点G，‎ 则由①的方法可得， 在Rt△GOD中，，DO=5，‎ ‎∴，，‎ 在Rt△GAD中，，∴ （ 3分）‎ 综上得 崇明区 ‎25．（本题满分14分，第(1)小题4分，第(2)小题4分，第(3)小题6分）‎ 如图，已知中，，，，D是AC边上一点，且，联结BD，点E、F分别是BC、AC上两点（点E不与B、C重合），，AE与BD相交于点G．‎ ‎（1）求证：BD平分；‎ ‎（2）设，，求与之间的函数关系式；‎ ‎（3）联结FG，当是等腰三角形时，求BE的长度．‎ ‎（备用图）‎ A B C D ‎（第25题图）‎ A B C D G E F ‎25．（满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）‎ ‎（1）∵， 又∵‎ ‎ ∴ ∴ ……………………………1分 ‎∵ ∴‎ 又∵是公共角 ∴ …………………………1分 ‎∴，‎ ‎∴ ∴ ∴ ………………………1分 ‎∴ ∴平分 ………………………1分 ‎（2）过点作交的延长线于点 ‎∵ ∴‎ ‎∵， ∴ ∴ ……1分 ‎∵ ∴ ∴ ∴…1分 ‎∵ 即 ‎∵ ∴ 又∵‎ ‎∴ ……………………………………………………………1分 ‎∴ ∴ ‎ ‎∴ …………………………………………………………1分 ‎（3）当△是等腰三角形时，存在以下三种情况：‎ ‎ 1° 易证 ，即，得到 ………2分 ‎ 2° 易证，即， …………2分 ‎ 3° 易证 ，即 ………2分 ‎ ‎ 奉贤区 ‎25．（本题满分14分，第(1)小题满分5分，第(2)小题满分5分，第(3)小题满分4分）‎ 已知：如图9，在半径为2的扇形AOB中，∠AOB=90°，点C在半径OB上，AC的垂直平分线交OA于点D，交弧AB于点E，联结BE、CD．‎ ‎（1）若C是半径OB中点，求∠OCD的正弦值； ‎ ‎（2）若E是弧AB的中点，求证：；‎ ‎（3）联结CE，当△DCE是以CD为腰的等腰三角形时，求CD的长．‎ 图9‎ A B C D O E 备用图 A B O 备用图 A B O 黄浦区 ‎25．（本题满分14分）‎ ‎ 如图，四边形ABCD中，∠BCD=∠D=90°，E是边AB的中点.已知AD=1，AB=2.‎ ‎ （1）设BC=x，CD=y，求y关于x的函数关系式，并写出定义域；‎ ‎ （2）当∠B=70°时，求∠AEC的度数；‎ ‎ （3）当△ACE为直角三角形时，求边BC的长.‎ ‎25. 解：（1）过A作AH⊥BC于H，————————————————————（1分）‎ ‎ 由∠D=∠BCD=90°，得四边形ADCH为矩形.‎ ‎ 在△BAH中，AB=2，∠BHA=90°，AH=y，HB=，‎ ‎ 所以，——————————————————————（1分）‎ 则.———————————————（2分）‎ ‎ ‎ ‎（2）取CD中点T，联结TE，————————————————————（1分）‎ ‎ 则TE是梯形中位线，得ET∥AD，ET⊥CD.‎ ‎ ∴∠AET=∠B=70°. ———————————————————————（1分）‎ ‎ 又AD=AE=1，‎ ‎ ∴∠AED=∠ADE=∠DET=35°. ——————————————————（1分）‎ ‎ 由ET垂直平分CD，得∠CET=∠DET=35°，————————————（1分）‎ ‎ 所以∠AEC=70°＋35°=105°. ——————————————————（1分）‎ ‎ （3）当∠AEC=90°时，‎ ‎ 易知△CBE≌△CAE≌△CAD，得∠BCE=30°，‎ ‎ 则在△ABH中，∠B=60°，∠AHB=90°，AB=2，‎ ‎ 得BH=1，于是BC=2. ——————————————————————（2分）‎ ‎ 当∠CAE=90°时，‎ ‎ 易知△CDA∽△BCA，又，‎ ‎ 则（舍负）—————（2分）‎ ‎ 易知∠ACE<90°.‎ ‎ 所以边BC的长为2或.——————————————————（1分）‎ 金山区 ‎25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5 分）‎ 如图9，已知在梯形ABCD中，AD∥BC，AB=DC=AD=5，，P是线段BC上 一点，以P为圆心，PA为半径的⊙P与射线AD的另一个交点为Q，射线PQ与射线 CD相交于点E，设BP=x．‎ ‎（1）求证△ABP∽△ECP；‎ ‎（2）如果点Q在线段AD上（与点A、D不重合），设△APQ的面积为y，‎ 求y关于x的函数关系式，并写出定义域；‎ ‎（3）如果△QED与△QAP相似，求BP的长． ‎ A B P C D Q E A B C D 图9‎ 备用图 ‎ ‎ ‎25．解：（1）在⊙P中，PA=PQ，∴∠PAQ ＝∠PQA，……………………………（1分）‎ ‎∵AD∥BC，∴∠PAQ ＝∠APB，∠PQA ＝∠QPC，∴∠APB ＝∠EPC，……（1分）‎ ‎∵梯形ABCD中，AD∥BC，AB=DC，∴∠B ＝∠C，…………………………（1分）‎ ‎∴△APB∽△ECP．…………………………………………………………（1分）‎ ‎（2）作AM⊥BC，PN⊥AD，‎ ‎∵AD∥BC，∴AM∥PN，∴四边形AMPN是平行四边形， ‎ ‎∴AM=PN，AN=MP．………………………………………………………（1分）‎ 在Rt△AMB中，∠AMB=90°，AB=5，sinB=，‎ ‎∴AM=3，BM=4，∴PN=3，PM=AN=x-4，……………………………………（1分）‎ ‎∵PN⊥AQ，∴AN=NQ，∴AQ= 2x-8，……………………………………（1分）‎ ‎∴，即，………………………（1分）‎ 定义域是．………………………………………………………（1分）‎ ‎（3）解法一：由△QED 与△QAP相似，∠AQP＝∠EQD，‎ ‎①如果∠PAQ＝∠DEQ，∵△APB∽△ECP，∴∠PAB＝∠DEQ，‎ 又∵∠PAQ＝∠APB，∴∠PAB＝∠APB，∴BP=BA=5．………………………（2分）‎ ‎②如果∠PAQ＝∠EDQ，∵∠PAQ＝∠APB，∠EDQ＝∠C，∠B＝∠C，‎ ‎∴∠B＝∠APB，∴ AB=AP，∵AM⊥BC，∴ BM=MP=4，∴ BP=8．………（2分）‎ 综上所述BP的长为5或者8．………………………………………………（1分）‎ 解法二：由△QAP与△QED相似，∠AQP＝∠EQD，‎ 在Rt△APN中，，‎ ‎∵QD∥PC，∴，‎ ‎∵△APB∽△ECP，∴，∴，‎ ‎①如果，∴，即，‎ 解得………………………………………………………………………（2分）‎ ‎②如果，∴，即，‎ 解得………………………………………………………………………（2分）‎ 综上所述BP的长为5或者8．…………………………………………………（1分）‎ 静安区 ‎25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）‎ A 第25题图 B P O C D E ‎·‎ ‎ 如图，平行四边形ABCD中，已知AB=6，BC=9，．对角线AC、BD交于点O．动点P在边AB上，⊙P经过点B,交线段PA于点E．设BP= x．‎ （1） 求AC的长；‎ （2） 设⊙O的半径为y，当⊙P与⊙O外切时，‎ 求y关于x的函数解析式，并写出定义域；‎ 第25题备用图 A B O C D （3） 如果AC是⊙O的直径，⊙O经过点E，‎ 求⊙O与⊙P的圆心距OP的长．‎ ‎ ‎ ‎25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）‎ A ‎·‎ 第25题图(1)‎ B P O C H E D 解：（1）作AH⊥BC于H，且，AB=6，‎ 那么…………（2分）‎ BC=9，HC=9-2=7，‎ ‎， ……………………（1分）‎ ‎﹒ ………（1分）‎ ‎·‎ A 第25题图(2)‎ B P O C D H E I ‎（2）作OI⊥AB于I，联结PO, AC=BC=9，AO=4.5‎ ‎∴∠OAB=∠ABC, ‎ ‎∴Rt△AIO中， ‎ ‎∴AI=1.5，IO= ……………………（1分）‎ ‎∴PI=AB-BP-AI=6-x-1.5=， ……………………（1分）‎ ‎∴Rt△PIO中，‎ ‎……（1分）‎ ‎∵⊙P与⊙O外切，∴ ……………………（1分）‎ ‎∴= …………………………（1分）‎ ‎∵动点P在边AB上，⊙P经过点B,交线段PA于点E．∴定义域：0 90o．‎ 与∠ACD =∠CDB = 90o矛盾．‎ ‎∴四边形ABDC不可能为直角梯形．…………………………（2分）‎ 普陀区 ‎25．（本题满分14分）‎ ‎ 已知是的直径延长线上的一个动点，的另一边交于点C、D，两点位于AB的上方，＝6，，，如图11所示．另一个半径为6的经过点C、D，圆心距．‎ ‎（1）当时，求线段的长；‎ ‎（2）设圆心在直线上方，试用的代数式表示；‎ ‎（3）△在点P的运动过程中，是否能成为以为腰的等腰三角形，如果能，试求出此时的值；如果不能，请说明理由．‎ O A B 备用图 P D O A B C 图11‎ ‎25．解：‎ ‎（1）过点作⊥，垂足为点，联结．‎ 在Rt△中，∵，，∴． （1分）‎ ‎ ∵＝6，∴． （1分）‎ ‎ 由勾股定理得 ． （1分）‎ ‎∵⊥，∴． （1分）‎ ‎（2）在Rt△中，∵，，∴． （1分）‎ 在Rt△中，． （1分）‎ 在Rt△中，． （1分）‎ 可得 ，解得． （2分）‎ ‎（3）△成为等腰三角形可分以下几种情况：‎ ‎● 当圆心、在弦异侧时 ‎①，即，由解得． （1分）‎ 即圆心距等于、的半径的和，就有、外切不合题意舍去． （1分）‎ ‎②，由，‎ 解得，即，解得． （1分）‎ ‎● 当圆心、在弦同侧时,同理可得 ．‎ ‎∵是钝角，∴只能是，即，解得． （2分）‎ 综上所述，的值为或．‎ 青浦区 ‎25.（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）‎ 如图9-1，已知扇形MON的半径为，∠MON=，点B在弧MN上移动，联结BM，作ODBM，垂足为点D，C为线段OD上一点，且OC=BM，联结BC并延长交半径OM于点A，设OA= x，∠COM的正切值为y． ‎ ‎（1）如图9-2，当ABOM时，求证：AM =AC；‎ ‎（2）求y关于x的函数关系式，并写出定义域；‎ ‎（3）当△OAC为等腰三角形时，求x的值. ‎ 图9-1‎ 图9-2‎ 备用图 ‎ ‎ ‎ ‎ ‎ ‎ ‎25．解：（1）∵OD⊥BM，AB⊥OM，∴∠ODM =∠BAM =90°． （1分）‎ ‎ ∵∠ABM +∠M =∠DOM +∠M，∴∠ABM =∠DOM． （1分）‎ ‎∵∠OAC=∠BAM，OC =BM，‎ ‎∴△OAC≌△ABM， （1分）‎ ‎∴AC =AM． （1分）‎ ‎（2）过点D作DE//AB，交OM于点E． （1分）‎ ‎∵OB＝OM，OD⊥BM，∴BD＝DM． （1分）‎ ‎∵DE//AB，‎ ‎∴，∴AE＝EM， ‎ ‎∵OM=，∴AE＝． （1分）‎ ‎∵DE//AB，‎ ‎∴， （1分）‎ ‎∴，‎ ‎∴．（） （2分）‎ ‎（3）（i） 当OA=OC时， ‎ ‎ ∵，‎ 在Rt△ODM中，．∵，‎ ‎∴．解得，或（舍）． （2分）‎ ‎（ii）当AO=AC时，则∠AOC =∠ACO，‎ ‎∵∠ACO >∠COB，∠COB =∠AOC，∴∠ACO >∠AOC，‎ ‎∴此种情况不存在． （1分）‎ ‎（ⅲ）当CO=CA时，‎ ‎ 则∠COA =∠CAO=，‎ ‎∵∠CAO >∠M，∠M=，∴>，∴>，‎ ‎∴，∵，∴此种情况不存在． （1分）‎ 松江区 ‎25．（本题满分14分，第（1）小题4分，第（2）小题每个小题各5分）‎ ‎ 如图，已知Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以点C为圆心、CB为半径的圆交AB于点D，过点A作AE∥CD，交BC延长线于点E.‎ ‎ （1）求CE的长；‎ ‎ （2）P是 CE延长线上一点，直线AP、CD交于点Q.‎ ① 如果△ACQ ∽△CPQ，求CP的长；‎ ‎(备用图)‎ C B A D E ‎(第25题图)‎ C B A D E ② 如果以点A为圆心，AQ为半径的圆与⊙C相切，求CP的长.‎ ‎25．（本题满分14分，第（1）小题4分，第（2）小题每个小题各5分）‎ ‎(第25题图)‎ C B A D E 解：（1）∵AE∥CD ‎∴…………………………………1分 ‎∵BC=DC ‎∴BE=AE …………………………………1分 设CE=x 则AE=BE=x+2‎ ‎∵ ∠ACB=90°，‎ ‎∴ ‎ 即………………………1分 C B A D E P Q ‎∴‎ 即…………………………………1分 ‎（2）①‎ ‎∵△ACQ ∽△CPQ，∠QAC>∠P ‎∴∠ACQ=∠P…………………………………1分 又∵AE∥CD ‎∴∠ACQ=∠CAE ‎∴∠CAE=∠P………………………………1分 ‎∴△ACE ∽△PCA，…………………………1分 ‎∴…………………………1分 即 ‎∴ ……………………………1分 ②设CP=t，则 ‎ ‎∵∠ACB=90°，‎ ‎∴ ‎ ‎∵AE∥CD ‎∴……………………………1分 即 ‎∴……………………………1分 若两圆外切，那么 此时方程无实数解……………………………1分 若两圆内切切，那么 ‎∴ ‎ 解之得………………………1分 又∵‎ ‎∴………………………1分 徐汇区 ‎25. 已知四边形是边长为10的菱形，对角线、相交于点，过点作∥交延长线于点，联结交于点.‎ ‎（1）如图1，当时，求的长；‎ ‎（2）如图2，以为直径作⊙，⊙经过点交边于点（点、‎ 不重合），设的长为，的长为；‎ ‎① 求关于的函数关系式，并写出定义域；‎ ① ‎ 联结，当是以为腰的等腰三角形时，求的长.‎ 杨浦区 ‎25、（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）‎ 如图9，在梯形ABCD中，AD//BC,AB=DC=5，AD=1，BC=9，点P为边BC上一动点，作PH⊥‎ DC，垂足H在边DC上，以点P为圆心PH为半径画圆，交射线PB于点E.‎ （1） 当圆P过点A时，求圆P的半径；‎ （2） 分别联结EH和EA，当△ABE△CEH时，以点B为圆心，r为半径的圆B与圆P相交，试求圆B的半径r的取值范围；‎ （3） 将劣弧沿直线EH翻折交BC于点F，试通过计算说明线段EH和EF的比值为定值，并求出此定值。‎