- 2021-05-22 发布 |
- 37.5 KB |
- 8页

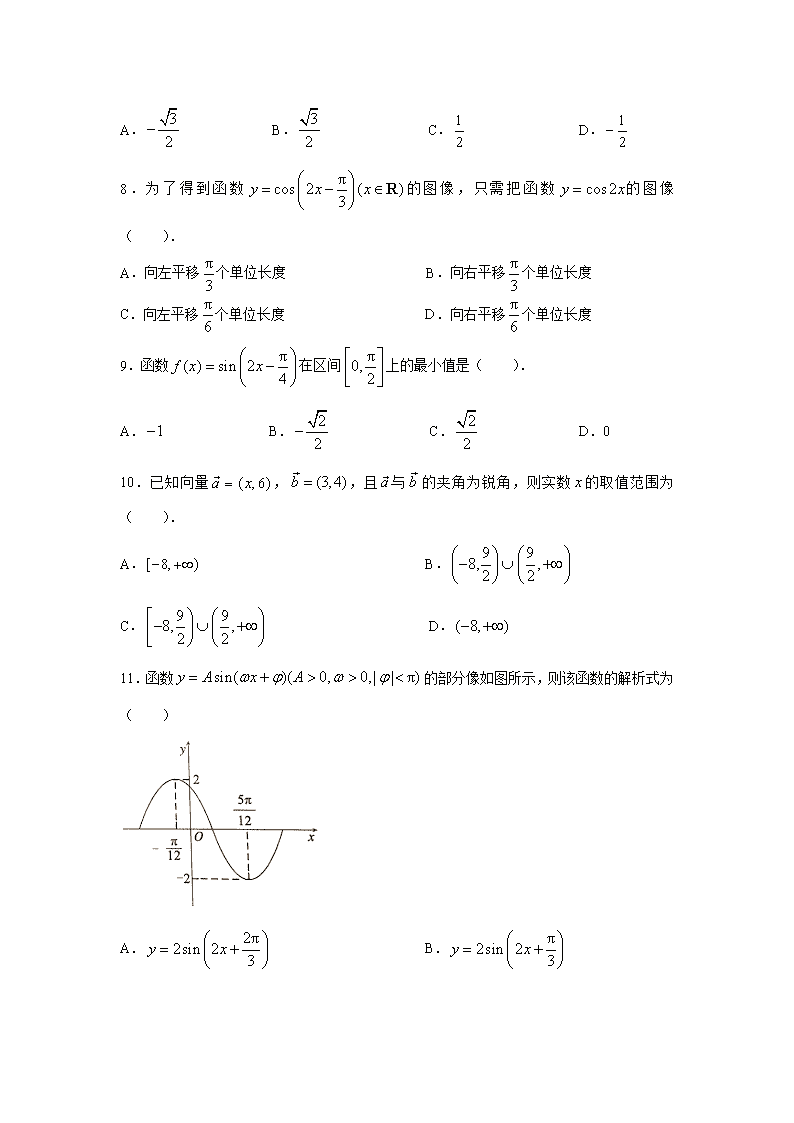

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】辽宁省辽阳市2019-2020学年高一下学期期中考试数学试题
辽宁省辽阳市2019-2020学年高一下学期期中考试数学试题 考生注意: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟. 2.请将各题答案填写在答题卡上. 第Ⅰ卷 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知一个扇形的弧长和半径都等于2,则这个扇形的面积为( ). A.2 B.3 C.4 D.6 2.已知且,则的终边落在( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.在中,,,,则( ). A. B. C. D. 4.已知,,则的值为( ). A. B. C. D. 5.已知,则的值为( ). A. B. C. D. 6.函数的单调递增区间是( ). A., B., C., D., 7.( ). A. B. C. D. 8.为了得到函数的图像,只需把函数的图像( ). A.向左平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移个单位长度 9.函数在区间上的最小值是( ). A. B. C. D.0 10.已知向量,,且与的夹角为锐角,则实数的取值范围为( ). A. B. C. D. 11.函数的部分像如图所示,则该函数的解析式为( ) A. B. C. D. 12.在中,面积,则( ). A. B. C. D. 第Ⅱ卷 二、填空题:本大题共4小题,每小题5分,其中第16小题第一空2分,第二空3分,共20分.把答案填在答题卡中的横线上. 13.已知,,若,则实数________. 14.方程,的解集为________. 15.已知,,则________. 16.函数的最小正周期为________,最大值为________. 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本题满分10分) 已知,且是第四象限角. (1)求的值; (2)求的值. 18.(本题满分12分) 已知向量,,且. (1)求向量与的夹角; (2)求的值. 19.(本题满分12分) 已知,. (1)求的值; (2)求的值. 20.(本题满分12分) 在中,内角,,所对的边分别为,,,已知. (1)求角的大小; (2)若,的面积为,求的周长. 21.(本题满分12分) 在中,内角,,所对的边分别为,,,且. (1)证明:; (2)若,且,求的值. 22.(本题满分12分) 为了迎接旅游旺季的到来,辽阳汤河风景区内供游客住宿的某宾馆,工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,现每年各个月份来宾馆入住的游客人数会呈现周期性的变化,并且有以下规律: ①每年相同的月份,入住宾馆的游客人数基本相同; ②入住宾馆的游客人数在2月份最少,在8月份最多,相差约400人; ③2月份入住宾馆的游客约为100人,随后逐月增加直到8月份达到最多. (1)若一年中入住宾馆的游客人数与月份之间的关系为,且.试求出函数的解析式; (2)请问哪几个月份要准备不少于400份的食物? 【参考答案】 一、选择题 1.A 2.D 3.A 4.C 5.C 6.C 7.B 8.D 9.B 10.B 11.A 12.D 二、填空题 13.1 14. 15. 16. 三、解答题 17.解:(1)因为是第四象限角,所以, 又,所以; 5分 (2) 10分 (注:结果正确满分;结果错误,诱导公式每正确一个得1分) 18.解:(Ⅰ)由得, 2分 因 ∴ ∴,向量与的夹角为 6分 (Ⅱ) 12分 19.解:(1)∵, ∴, ∴. 6分 (2)由题意得 12分 20.(Ⅰ)由正弦定理,得 , 2分 在中,因为,所以 故, 4分 又因为,所以. 6分 (Ⅱ)由已知,得. 又,所以. 8分 由已知及余弦定理,得, 所以,从而.即 10分 又, 所以的周长为 12分 21.(1)证明:由正弦定理 得,,,代入 2分 即 又,所以 4分 因为,所以 因为,是三角形的内角,所以 6分 (2)由(1)知,所以,从而 8分 因为,所以,∴ 10分 故 11分 ∵,∴ 12分 22.解:(1)因为, 且 根据条件①,可知这个函数的周期是12; 2分 由②可知,最小,最大,且; 由③可知,函数在上单调递增,且,所以. 根据上述分析可得,,故, 且,解得 4分 根据分析可知,当时,取最小值,当时,取最大值. 故,且, 又因为,故 5分 所以入住宾馆的游客人数与月份之间的关系式为,且; 6分 (2)令, 化简得, 8分 即, 解得. 因为,且,所以, 11分 即在6月、7月、8月、9月、10月5个月份要准备不少于400份的食物. 12分查看更多