2020年高考物理一轮复习 第4章 试题解析19

2020年高考物理一轮复习 第4章 试题解析19

学案19　圆周运动规律的应用 ‎ 吗 一、概念规律题组 ‎1．铁路转弯处的圆弧半径为R，内侧和外侧的高度差为h，L为两轨间的距离，且L>h.如果列车转弯速率大于，则(　　)‎ A．外侧铁轨与轮缘间产生挤压 B．铁轨与轮缘间无挤压 C．内侧铁轨与轮缘间产生挤压 D．内、外铁轨与轮缘间均有挤压 图1‎ ‎2．一辆卡车在丘陵地区匀速行驶，地形如图1所示，由于轮胎太旧，途中爆胎，爆胎可能性最大的地段应是(　　)‎ A．a处 B．b处 C．c处 D．d处 ‎3．下列说法中正确的是(　　)‎ A．当物体受到离心力的作用时，物体将做离心运动 B．当物体所受的离心力大于向心力时产生离心现象 C．做匀速圆周运动的物体，当它所受的一切力都突然消失时，它将背离圆心，沿着半径方向“背心”而去 D．做匀速圆周运动的物体，当它所受的一切力都突然消失时，它将沿这一位置的切线方向飞出，做匀速直线运动 图2‎ ‎4．如图2所示，已知mA＝2mB＝3mC，它们之间距离的关系是rA＝rC＝rB，三物体与转盘表面的动摩擦因数相同，当转盘的转速逐渐增大时(　　)‎ A．物体A先滑动 B．物体B先滑动 C．物体C先滑动 D．B与C同时开始滑动 二、思想方法题组 ‎5．一轻杆的一端固定质量为m的小球，以另一端为圆心在竖直平面内做圆周运动，轻杆长为l，以下说法中正确的是(　　)‎ A．小球过最高点时，杆的弹力不可以等于零 B．小球过最高点时的最小速度为 C．小球到最高点时速度v>0，小球一定能通过最高点做圆周运动 D．小球过最高点时，杆对球的作用力一定与小球所受重力方向相反 11‎ 图3‎ ‎6．如图3所示，用细绳拴着质量为m的物体，在竖直面内做圆周运动，圆周半径为R，则下列说法正确的是(　　)‎ A．小球过最高点时，绳子张力不可以为零 B．小球过最高点时的最小速度为零 C．小球刚好过最高点时的速度是 D．小球过最高点时，绳子对小球的作用力可以与球所受的重力方向相反 ‎ 圆周运动规律在实际中的应用 ‎1．圆锥摆类问题分析 图4‎ 圆锥摆是一种典型的匀速圆周运动模型，基本的圆锥摆模型和受力情况如图4所示，拉力(或弹力)和重力的合力提供球做圆周运动的向心力．‎ F合＝Fn＝mgtan θ＝m 其运动情况也相似，都在水平面内做圆周运动，圆心在水平面内，常见的圆锥摆类模型还有：火车转弯(如图5所示)；杂技节目“飞车走壁”(如图6所示)；飞机在水平面内的盘旋(如图7所示)‎ ‎　　‎ ‎　　　图5　　　　　　　图6‎ 图7‎ 11‎ 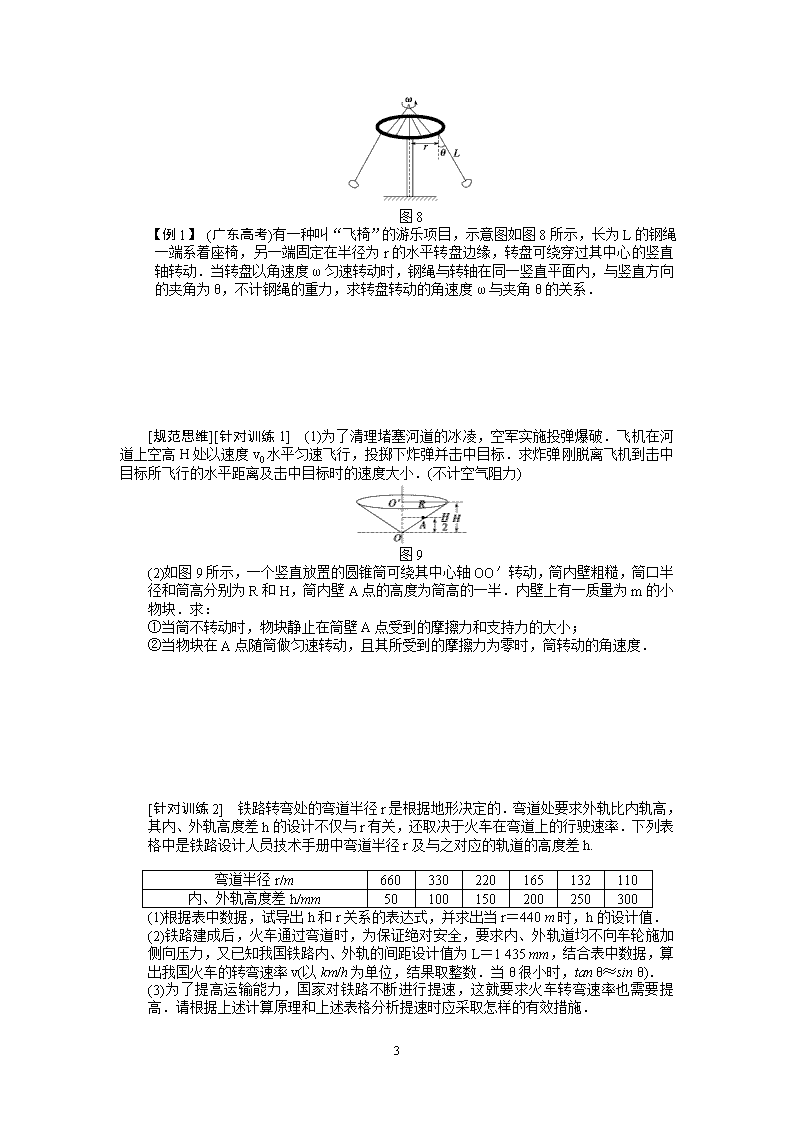图8‎ ‎【例1】 (广东高考)有一种叫“飞椅”的游乐项目，示意图如图8所示，长为L的钢绳一端系着座椅，另一端固定在半径为r的水平转盘边缘，转盘可绕穿过其中心的竖直轴转动．当转盘以角速度ω匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ，不计钢绳的重力，求转盘转动的角速度ω与夹角θ的关系．‎ ‎[规范思维][针对训练1]　(1)为了清理堵塞河道的冰凌，空军实施投弹爆破．飞机在河道上空高H处以速度v0水平匀速飞行，投掷下炸弹并击中目标．求炸弹刚脱离飞机到击中目标所飞行的水平距离及击中目标时的速度大小．(不计空气阻力)‎ 图9‎ ‎(2)如图9所示，一个竖直放置的圆锥筒可绕其中心轴OO′转动，筒内壁粗糙，筒口半径和筒高分别为R和H，筒内壁A点的高度为筒高的一半．内壁上有一质量为m的小物块．求：‎ ‎①当筒不转动时，物块静止在筒壁A点受到的摩擦力和支持力的大小；‎ ‎②当物块在A点随筒做匀速转动，且其所受到的摩擦力为零时，筒转动的角速度．‎ ‎[针对训练2]　铁路转弯处的弯道半径r是根据地形决定的．弯道处要求外轨比内轨高，其内、外轨高度差h的设计不仅与r有关，还取决于火车在弯道上的行驶速率．下列表格中是铁路设计人员技术手册中弯道半径r及与之对应的轨道的高度差h.‎ 弯道半径r/m ‎660‎ ‎330‎ ‎220‎ ‎165‎ ‎132‎ ‎110‎ 内、外轨高度差h/mm ‎50‎ ‎100‎ ‎150‎ ‎200‎ ‎250‎ ‎300‎ ‎(1)根据表中数据，试导出h和r关系的表达式，并求出当r＝440 m时，h的设计值．‎ ‎(2)铁路建成后，火车通过弯道时，为保证绝对安全，要求内、外轨道均不向车轮施加侧向压力，又已知我国铁路内、外轨的间距设计值为L＝1 435 mm，结合表中数据，算出我国火车的转弯速率v(以km/h为单位，结果取整数．当θ很小时，tan θ≈sin θ)．‎ ‎(3)为了提高运输能力，国家对铁路不断进行提速，这就要求火车转弯速率也需要提高．请根据上述计算原理和上述表格分析提速时应采取怎样的有效措施．‎ 11‎ ‎2．竖直面内的圆周运动问题分析 图10‎ ‎(1)绳(单轨，无支撑，水流星模型)：绳只能给物体施加拉力，而不能有支持力(如图10所示)．‎ 这种情况下有F＋mg＝≥mg，所以小球通过最高点的条件是v≥，通过最高点的最小速度vmin＝.‎ ‎①当v> 时，绳对球产生拉力，轨道对球产生压力．‎ ‎②当v< 时，球不能通过最高点(实际上球没有到最高点就脱离了轨道．)‎ 图11‎ ‎(2)外轨(单轨，有支撑，汽车过拱桥模型)，只能给物体支持力，而不能有拉力(如图11所示)．‎ 有支撑的汽车，弹力只可能向上，在这种情况下有：‎ mg－F＝≤mg，‎ 所以v≤，‎ 物体经过最高点的最大速度vmax＝，‎ 此时物体恰好离开桥面，做平抛运动．‎ ‎(3)杆(双轨，有支撑)：对物体既可以有拉力，也可以有支持力，如图12所示．‎ 图12‎ ‎①过最高点的临界条件：v＝0.‎ ‎②在最高点，如果小球的重力恰好提供其做圆周运动的向心力，即mg＝，v＝，杆或轨道内壁对小球没有力的作用．‎ 当0时，小球受到重力和杆向下的拉力(或外轨道对球向下的压力)．‎ 图13‎ ‎【例2】 如图13所示，位于竖直平面内的光滑轨道，由一段斜的直轨道和与之相切的圆形轨道连接而成，圆形轨道的半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动．要求物块能通过圆形轨道的最高点，且在该最高点与轨道间的压力不能超过5mg(g为重力加速度)．求物块初始位置相对于圆形轨道底部的高度h的取值范围．‎ 11‎ ‎[规范思维]‎ ‎　‎ ‎　‎ ‎　‎ 图14‎ ‎[针对训练3]　在2008年北京奥运会上，我国体操小将邹凯夺得单杠、自由体操、男子团体三枚金牌，以一届奥运会收获三金的佳绩与84年的体操王子李宁比肩．如图14所示为邹凯做单杠动作单臂大回旋的瞬间．他用一只手抓住单杠，伸展身体，以单杠为轴做圆周运动．假设他的质量为60 kg，要完成动作，则他运动到最低点时手臂受的拉力至少约为(忽略空气阻力，取g＝10 m/s2)(　　)‎ A．600 N B．2 400 N C．3 000 N D．3 600 N 图15‎ ‎[针对训练4]　如图15所示，小物块位于半径为R的半圆柱形物体顶端，若给小物块一水平速度v0＝，则物块(　　)‎ A．立即做平抛运动 B．落地时水平位移为R C．落地速度大小为2 D．落地时速度方向与地面成60°角 ‎【基础演练】‎ ‎1．如图16所示，‎ 图16‎ 质量为m的小球在竖直平面内的光滑圆环轨道上做圆周运动．圆环半径为R，小球经过圆环最高点时刚好不脱离圆环，则其通过最高点时，下列说法错误的是(　　)‎ A．小球对圆环的压力大小等于mg 11‎ B．小球受到的向心力等于重力mg C．小球的线速度大小等于 D．小球的向心加速度大小等于g 图17‎ ‎2．如图17所示，质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直固定放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的动摩擦因数为μ，则物体在最低点时，下列说法正确的是(　　)‎ A．受到向心力为mg＋m B．受到的摩擦力为μm C．受到的摩擦力为μ(mg＋m)‎ D．受到的合力方向斜向右上方 图18‎ ‎3．如图18所示，长为L的细绳一端固定，另一端系一质量为m的小球．给小球一个合适的初速度，小球便可在水平面内做匀速圆周运动，这样就构成了一个圆锥摆，设细绳与竖直方向的夹角为θ.下列说法正确的是(　　)‎ A．小球受重力、绳的拉力和向心力作用 B．小球只受重力和绳的拉力作用 C．θ越大，小球运动的速度越小 D．θ越大，小球运动的周期越大 ‎4．在高速公路的拐弯处，路面造得外高内低，即当车向右拐弯时，司机左侧的路面比右侧的要高一些，路面与水平面间的夹角为θ.设拐弯路段是半径为R的圆弧，要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零．θ应等于(　　)‎ A．arcsin B．arctan C.arcsin D．arccot 图19‎ ‎5．质量为m的飞机以恒定速率v在空中水平盘旋(如图19所示)，做匀速圆周运动的半径为R，重力加速度为g，则此时空气对飞机的作用力大小为(　　)‎ A．m B．mg C．m D．m ‎6．一根轻绳长0.5 m，它最多能承受140 N的拉力．在此绳一端系一质量为1 kg的小球，另一端固定，使小球在竖直面内做圆周运动，为维持此运动，小球在最高点处的速度大小取值范围是(　　)‎ A．0≤v≤5 m/s 11‎ B. m/s≤v≤3 m/s C．0≤v≤3 m/s D．3 m/s≤v≤5 m/s ‎7．‎ 图20‎ 水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切，一小球以初速度v0沿直轨道向右运动，如图20所示，小球进入半圆形轨道后刚好能通过c点，然后小球做平抛运动落在直轨道上的d点，则下列说法错误的是(　　)‎ A．小球到达c点的速度为 B．小球到达b点时对轨道的压力为5mg C．小球在直轨道上的落点d与b点距离为2R D．小球从c点落到d点所需时间为2 图21‎ ‎8．如图21所示，在竖直的转动轴上，a、b两点间距为40 cm，细线ac长50 cm，bc长30 cm，在c点系一质量为m的小球，在转动轴带着小球转动的过程中，下列说法不正确的是(　　)‎ A．转速小时，ac受拉力，bc松弛 B．bc刚好拉直时ac中拉力为1.25mg C．bc拉直后转速增大，ac拉力不变 D．bc拉直后转速增大，ac拉力增大 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 ‎【能力提升】‎ ‎9．如图22所示，在水平匀速运动的传送带的左端(P点)，轻放一质量为m＝1 kg的物块，物块随传送带运动到A点后水平抛出，物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、D为圆弧的两端点，其连线水平．已知圆弧半径R＝1.0 m，圆弧对应的圆心角θ＝106°，轨道最低点为C点，A点距水平面的高度h＝0.8 m．(g取10 m/s2，sin 53°＝0.8，cos 53°＝0.6)求：‎ ‎(1)物块离开A点时水平初速度的大小；‎ ‎(2)物块经过C点时对轨道压力的大小；‎ ‎(3)设物块与传送带间的动摩擦因数为0.3，传送带的速度为5 m/s，求PA间的距离．‎ 图22‎ 11‎ 图23‎ ‎10．小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动．当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地，如图23所示．已知握绳的手离地面高度为d，手与球之间的绳长为d，重力加速度为g.忽略手的运动半径、绳重和空气阻力．‎ ‎(1)求绳断时球的速度大小v1和球落地时的速度大小v2.。‎ ‎(2)问绳能承受的最大拉力多大？‎ ‎(3)改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？‎ 学案19　圆周运动规律的应用 ‎【课前双基回扣】‎ ‎1．A ‎2．D　[车胎在凹部受到的支持力FN＝mg＋m大于在凸部受到的支持力FN＝mg－m.所以汽车在凹部b、d两处爆胎可能性大，但d处的曲率半径小于b处的曲率半径，汽车以同样的速率经过b、d两处时，根据FN＝mg＋m可知，在d处爆胎的可能性最大，D正确．]‎ ‎3．D　[物体实际上并不受向心力的作用，离心运动也不是由于物体受到“离心力”的作用而出现的，而是惯性的表现，做圆周运动的物体，在向心力突然消失或合力不足以提供物体做圆周运动所需的向心力时，物体将做远离圆心的运动，因此选项A、B均是错误的；物体做匀速圆周运动时，当它所受的一切力都突然消失，即物体所受的合外力突然变为零时，根据牛顿第一定律，物体将从这一时刻起沿这一位置的切线方向飞出，做匀速直线运动，而不是背离圆心，沿着半径方向“背心”而去，故选项C错误．]‎ ‎4．B　[A、B、C三个物体做圆周运动的ω相同，静摩擦力提供向心力，由牛顿第二定律可得μmg＝mω2r，当角速度ω增大时，半径r越大，越易滑动．]‎ ‎5．AC　[对轻杆一端的小球过最高点时的速度可能为0，当小球到最高点的速度v＝时杆的弹力等0，故A正确；当v<时，杆对球的作用力为支持力；当v>时，杆对球的作用力为拉力，拉力的方向与重力的方向相同，故D错]‎ ‎6．AC　[小球过最高点时的临界速度v＝，此时绳中张力为零．小球过最高点时绳子中的张力可能为零，也可能向下，故答案为A、C.]‎ 思维提升 ‎1．虽然铁路外轨高于内轨，但整个外轨是等高的，整个内轨是等高的．因而火车在行驶的过程中，重心的高度不变，即火车重心的轨迹在同一水平面内．故火车运动轨迹的圆周平面是水平面，而不是斜面。‎ ‎2．汽车通过凹部时处于超重状态；通过凸部时处于失重状态．‎ ‎3．离心运动是因为所受的向心力小于所需向心力所致，根本不存在“离心力”‎ 11‎ 这种力．‎ 离心运动轨迹可以是直线，也可以是曲线．‎ ‎4．杆连小球与绳连小球在完成竖直面内的圆周运动时，所需临界条件不同．其根本原因是杆可提供拉力，也可提供支持力，而绳只能提供拉力．‎ ‎【核心考点突破】‎ 例1 解析　设转盘转动角速度为ω时，钢绳与竖直方向的夹角为θ 座椅到中心轴的距离：R＝r＋Lsin θ①‎ 对座椅受力分析有：Fn＝mgtan θ＝mRω2②‎ 联立①②两式得：ω＝ 例2 R≤h≤5R 解析　设物块在圆形轨道最高点的速度为v，由机械能守恒得mgh＝2mgR＋mv2①‎ 物块在最高点受的力为重力mg、轨道的压力FN.重力与压力的合力提供向心力，有mg＋FN＝m②‎ 物块能通过最高点的条件是FN≥0，即当FN＝0，只有重力提供向心力时为通过最高点的临界条件，有mg≤m③‎ 由②③式可得v≥④‎ 由①④式得h≥R⑤‎ 按题的要求，FN≤5mg，代入②式得v≤⑥‎ 由①⑥式得h≤5R⑦‎ ‎[规范思维]　解此题要注意两个临界条件的分析，特别要理解“物块能通过最高点”的临界条件的意义。‎ ‎[针对训练]‎ ‎1．(1)v0　 ‎(2)①　　② ‎2．(1)hr＝33 m2　75 mm　(2)54 km/h　(3)见解析 ‎3．C ‎4．AC　[物体恰好不受轨道的支持力的情况下(物体在最高点做圆周运动)的临界条件是最高点速度为，因为v0＝>，所以物体将从最高点开始做平抛运动，A正确；由平抛运动的规律R＝gt2，x＝v0t，可得：x＝2R，B答案错误；落地时竖直分速度vy＝，合速度v＝＝2，其方向与地面成45°角，C正确，D错误．]‎ ‎【课时效果检测】‎ ‎1．BCD　[小球经过最高点时刚好不脱离圆环，重力正好全部用来提供向心力，小球对圆环无压力，即Fn＝mg＝m＝ma，所以v＝，a＝g，故B、C、D正确．]‎ ‎2．CD　[物体在最低点受到竖直方向的合力Fy，方向向上，提供向心力，Fy＝m，A错误；由Fy＝FN－mg，得FN＝mg＋m，物体受到的滑动摩擦力Ff＝μFN＝μ(mg＋m)，B错误，C正确；Ff水平向左，故物体受到Ff与Fy的合力，斜向左上方，D正确．]‎ 11‎ ‎3.BC　‎ ‎[小球只受重力和绳的拉力作用，向心力是由两个力的合力提供的，故A错，B对；如右图所示，向心力Fn＝mgtan θ＝m＝mLsin θ，解得v＝，故θ越大，小球运动的速度越大，C对；T＝2π ，故θ越大，T越小，D错．]‎ ‎4．B ‎[汽车拐弯时，受到支持力和重力作用而做匀速圆周运动，两个力的合力方向指向水平圆周的圆心，根据牛顿第二定律：mgtan θ＝m，得θ＝arctan ，B正确．]‎ ‎5．C ‎[飞机在盘旋时在水平面内做匀速圆周运动，受到重力和空气的作用力两个力的作用，合力提供向心力Fn＝m.飞机运动情况和受力情况示意图如右图所示，根据平形四边形定则得：F＝＝m ，C正确．]‎ ‎6．B　[设小球在最高点的最小速度为v1，最大速度为v2.则在最高点：mg＝①‎ 在最低点：Fm－mg＝②由机械能守恒定律得mv＋mg·2l＝mv③由①②③得：v1＝ m/s，v2＝3 m/s.所以答案B正确．]‎ ‎7．ACD　[小球在c点时由牛顿第二定律得：mg＝，vc＝，A项正确；‎ 小球由b点运动到c点的过程中，由机械能守恒定律得：mv＝2mgR＋mv 小球在b点，由牛顿第二定律得：FN－mg＝，联立解得FN＝6mg，B项错误；‎ 小球由c点平抛，在平抛运动过程中由运动学公式得：‎ x＝vct,2R＝gt2.解得t＝2 ，x＝2R，C、D项均正确．]‎ ‎8．D ‎9．(1)3 m/s　(2)43 N　(3)1.5 m 解析　(1)物块由A到B在竖直方向上有 v＝2gh代入数据，得vy＝4 m/s 11‎ 在B点tan ＝　解得：vA＝3 m/s ‎(2)物块由B到C由动能定理知mgR(1－cos )＝mv－mv 又vB＝＝5 m/s 解得：v＝33(m/s)2‎ 在C点由牛顿第二定律，得FN－mg＝m ，代入数据解得：FN＝43 N 由牛顿第三定律知，物块对轨道压力的大小为FN′＝FN＝43 N ‎(3)因物块到达A点时的速度为3 m/s，小于传送带速度，故物块在传送带上一直做匀加速直线运动．μmg＝ma a＝3 m/s2 PA间的距离xPA＝＝1.5 m.‎ ‎10．(1)v1＝　v2＝ 　(2)mg (3)　d 解析　(1)设绳断后球飞行时间为t，由平抛运动规律有竖直方向：d－d＝gt2，水平方向：d＝v1t联立解得v1＝.由机械能守恒定律有mv＝mv＋mg(d－d) 解得v2＝ .‎ ‎(2)设绳能承受的最大拉力大小为F，这也是球受到绳的最大拉力大小．‎ 球做圆周运动的半径为R＝d 由圆周运动向心力公式有F－mg＝ 联立解得F＝mg.‎ ‎(3)设绳长为l，绳断时球的速度大小为v3，绳承受的最大拉力不变，有F－mg＝m，得v3＝ .‎ 绳断后球做平抛运动，竖直位移为d－l，水平位移为x，‎ 时间为t1，有d－l＝gt，x＝v3t1‎ 解得x＝4 .‎ 当l＝时，x有极大值xm＝d.‎ 易错点评 ‎1．汽车过凸形拱桥面顶点，当汽车的速度v＝时，汽车对桥的压力减小为零．这时，汽车以速度v＝开始做平抛运动，而不再沿桥面做圆周运动，如图所示 ‎2．处理离心运动问题时，要注意区分外界所提供的力与物体做圆周运动所需的向心力。‎ ‎3．处理竖直面内的圆周运动时，要注意临界条件的使用，且在最高点或最低点时应用向心力关系，而在两点之间应用动能定理或功能关系处理。‎ ‎ ‎ 11‎