高考西工大附中第四次适应性训练数学试题

高考西工大附中第四次适应性训练数学试题

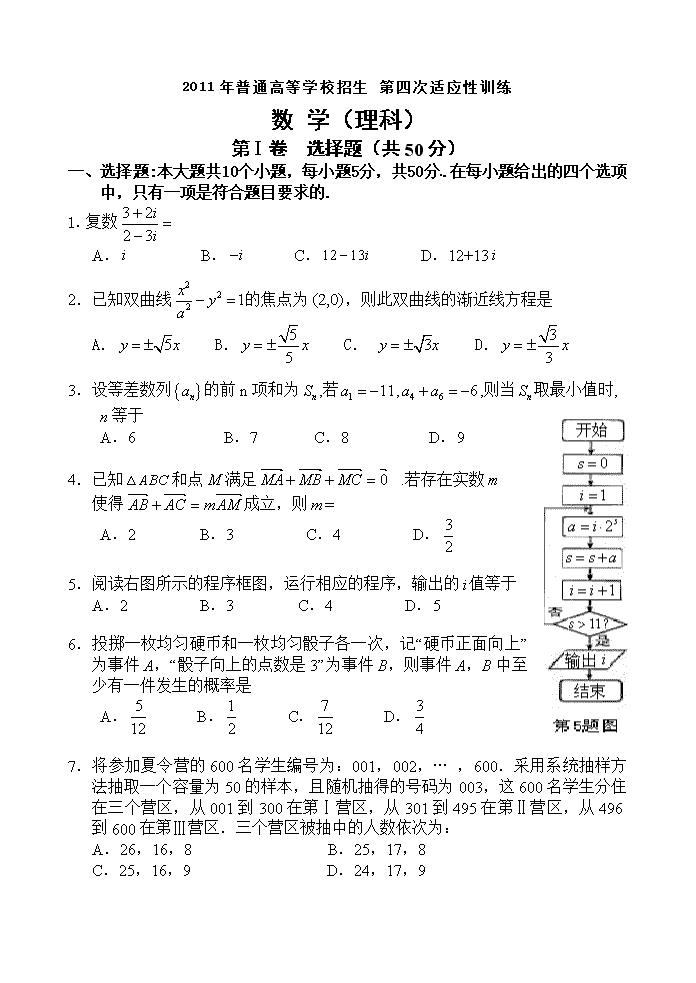
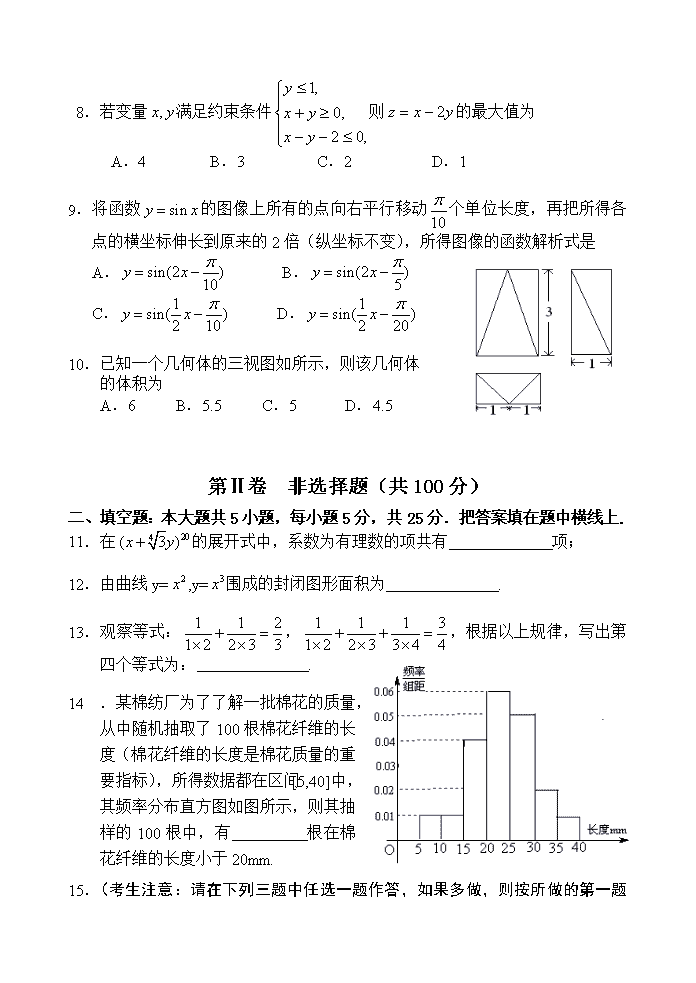
‎2011年普通高等学校招生 第四次适应性训练 数 学（理科）‎ 第Ⅰ卷 选择题（共50分）‎ 一、选择题:本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1 复数 A． B． C． D．12+13‎ ‎2．已知双曲线的焦点为，则此双曲线的渐近线方程是 ‎ A． B． C． D． ‎ ‎3．设等差数列的前n项和为,若,,则当取最小值时,‎ n等于 A．6 B．‎7 C．8 D．9‎ ‎4．已知和点满足.若存在实数 使得成立，则=‎ A．2 B．‎3 C．4 D．‎ ‎5．阅读右图所示的程序框图，运行相应的程序，输出的值等于 A．2 B．‎3 C．4 D．5‎ ‎6．投掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币正面向上”为事件A，“骰子向上的点数是‎3”‎为事件B，则事件A，B中至少有一件发生的概率是 A． B． C． D．‎ ‎7．将参加夏令营的600名学生编号为：001，002，… ，600．采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003，这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区．三个营区被抽中的人数依次为：‎ A．26，16，8 B．25，17，8‎ C．25，16，9 D．24，17，9‎ ‎ 8．若变量满足约束条件则的最大值为 A．4 B．‎3 C．2 D．1‎ ‎9．将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是 A． B．‎ C． D．‎ ‎10．已知一个几何体的三视图如所示，则该几何体 的体积为 A．6 B．‎5.5 C．5 D．4.5‎ 第Ⅱ卷 非选择题（共100分）‎ 二、填空题：本大题共5小题，每小题5分，共25分．把答案填在题中横线上.‎ ‎11．在的展开式中，系数为有理数的项共有 项；‎ ‎12．由曲线y=,y=围成的封闭图形面积为 .‎ ‎13．观察等式：，，根据以上规律，写出第四个等式为： .‎ ‎14．某棉纺厂为了了解一批棉花的质量， 从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有 根在棉花纤维的长度小于‎20mm.‎ ‎15．‎ ‎（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）‎ A. (不等式选做题)若关于x的不等式有解，则实数的取值范围是： .‎ B. (几何证明选做题)如图，四边形ABCD是 圆O 的内接四边形，延长AB和DC相交 于点P. 若，，则的值 为 .‎ C. (坐标系与参数方程选做题)设曲线的参数方程为（为参数），以原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为，则曲线上到直线距离为的点的个数为： .‎ 三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤.‎ ‎16. （本小题满分12分）‎ ‎、、为的三内角，且其对边分别为、b、c，若，，且．‎ ‎(Ⅰ) 求角；‎ ‎(Ⅱ) 若，三角形面积，求的值．‎ ‎17．（本小题满分12分）‎ 已知函数在x＝－与x＝1时都取得极值．‎ ‎(Ⅰ) 求、b的值与函数的单调递减区间；‎ ‎(Ⅱ) 若对，不等式恒成立，求c的取值范围．‎ ‎18．（本小题满分12分）‎ 某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示 ‎(Ⅰ) 求甲、乙两名运动员得分的中位数；‎ ‎（II）你认为哪位运动员的成绩更稳定？ ‎ ‎(Ⅲ) 如果从甲、乙两位运动员的7场得分中各 随机抽取一场的得分，求甲的得分大于乙 的得分的概率．（参考数据：，）‎ ‎19．（本小题满分12分）‎ 如图，四棱锥S-ABCD 的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点．‎ ‎(Ⅰ) 求证：AC⊥SD；‎ ‎(Ⅱ) 若SD⊥平面PAC，求二面角 P-AC-D的大小 ‎(Ⅲ) 在（Ⅱ）的条件下，侧棱SC上是 否存在一点E，使得BE∥平面PAC？若存在，求SE：EC的值；若不存在，试说明理由．‎ ‎20．（本小题满分13分）‎ 已知在数列中，，当时，其前项和满足．‎ ‎(Ⅰ) 求的表达式；‎ ‎(Ⅱ) 设，求数列的前项和．‎ ‎21．（本小题满分14分）‎ 已知椭圆E的中心在原点，焦点在x轴上，椭圆上的点到焦点的距离的最小值为，离心率e=．‎ ‎(Ⅰ) 求椭圆E的方程；‎ ‎(Ⅱ) 过点（1,0）作直线交E于P、Q两点，试问在x轴上是否存在一定点M，使为定值？若存在，求出定点M的坐标；若不存在，请说明理由．‎ ‎2011年普通高等学校招生 第四次适应性训练 数学（理科）参考答案与评分标准 一、选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A D A B C C B B C C 二、填空题: ‎ ‎11．6； 12．； 13．； 14．30．‎ ‎15（选做题）A．； B．； C．3．‎ 三、解答题：‎ ‎16．【解】：（1）∵，，且．‎ ‎∴即，又，．……（6分）‎ ‎（2） ，.‎ 又由余弦定理得：,‎ ‎，故．…………………………………（12分）‎ ‎17．解：（1）f（x）＝x3＋ax2＋bx＋c，f¢（x）＝3x2＋2ax＋b 由f¢（）＝，f¢（1）＝3＋‎2a＋b＝0得 a＝，b＝－2 …………………………（4分）‎ f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：‎ x ‎（－¥，－）‎ ‎－‎ ‎（－，1）‎ ‎1‎ ‎（1，＋¥）‎ f¢（x）‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f（x）‎ 极大值 ¯ 极小值 所以函数f（x）的递减区间是（－，1） …………………（8分）‎ ‎（2）f（x）＝x3－x2－2x＋c，xÎ〔－1，2〕，‎ 当x＝－时，f（x）＝＋c 为极大值，而f（2）＝2＋c，则f（2）＝2＋c为最大值。‎ 要使f（x）f（2）＝2＋c 解得c<－1或c>2………………………………………（12分）‎ ‎18.【解】：（1）运动员甲得分的中位数是22，运动员乙得分的中位数是23 ‎ ‎…………………………………………………………………………2分 ‎（2） …………3分 ‎ …………………4分 ‎ …5 ‎ ‎，从而甲运动员的成绩更稳定 ………………………………8分 ‎（3）从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49其中甲的得分大于乙的是：甲得14分有3场，甲得17分有3场，甲得15分有3场甲得24分有4场，甲得22分有3场，甲得23分有3场，甲得32分有7场，共计26场 ………………………………………11分 从而甲的得分大于乙的得分的概率为…………………………12分 ‎19．【解法一】：（Ⅰ）连BD，设AC交BD于O，由题意。在正方形ABCD中，，所以,得. ……………（4分）‎ ‎(Ⅱ)设正方形边长，则。又，所以,‎ 连，由（Ⅰ）知,所以,‎ 且,所以是二面角的平面角。‎ 由,知,所以,‎ 即二面角的大小为。 ……………………………（8分）‎ ‎（Ⅲ）在棱SC上存在一点E，使 由（Ⅱ）可得，故可在上取一点,使,过作的平行线与的交点即为。连BN。在中知，又由于,故平面，得,由于,故.‎ ‎ ……………………………………………………………………（12分）‎ ‎【解法二】：（Ⅰ）；连,设交于于，由题意知.以O为坐标原点，分别为轴、轴、轴正方向，建立坐标系 设底面边长为，则高。‎ 于是，，‎ ‎，，故 ，从而 ‎(Ⅱ)由题设知，平面的一个法向量，平面的一个法向量，设所求二面角为，则,所求二面角的大小为 ‎（Ⅲ）在棱上存在一点使.‎ 由（Ⅱ）知是平面的一个法向量，‎ 且 设则 而，即当时，，‎ 而不在平面内，故 ‎20．解：(1)当时，代人得：‎ ‎，‎ ‎∴…………………………………（6分）‎ ‎(2)‎ ‎∴= ………13分 ‎21．解：(1)，‎ ‎∴所求椭圆E的方程为： …………………（5分）‎ ‎(2)当直线不与x轴重合时，可设直线的方程为：‎ ‎ ， 把（2）代人（1）整理得：‎ ‎………（3）‎ ‎∴， ………………………………（8分）‎ 假设存在定点，使得为定值 ‎=‎ 当且仅当，即时，（为定值）．这时 ‎ ………………………………………………………………（12分）‎ 再验证当直线的倾斜角时的情形，此时取，‎ ‎，‎ ‎∴存在定点使得对于经过（1,0）点的任意一条直线 均有（恒为定值）． ………………‎