- 2021-05-22 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上册青岛版数学课件2-4解直角三角形
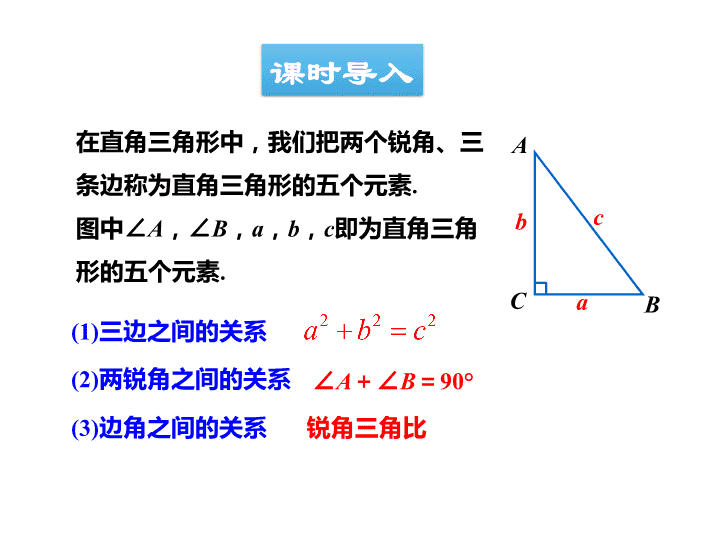
2.4解直角三角形 1.了解解直角三角形的含义. 2.经历解直角三角形的过程,掌握解直角三角形的方法. 学习目标 (2)两锐角之间的关系 ∠A+∠B=90° (3)边角之间的关系 (1)三边之间的关系 A Ba b c C 在直角三角形中,我们把两个锐角、三 条边称为直角三角形的五个元素. 图中∠A,∠B,a,b,c即为直角三角 形的五个元素. 锐角三角比 课时导入 A Ba b c C解直角三角形: 由直角三角形中已知元素求出未知元素的过程,叫作解 直角三角形. 一个直角三角形中,若已知五个 元素中的两个元素(其中必须有一个元 素是边),则这样的直角三角形可解. 感悟新知 知道五个元素中的几个,就可以求其余元素? 探究 必须已知除直角外的两个元素(至少有一个是边). 已知两边:a.两直角边;b.一直角边和斜边. 已知一边和一锐角:a.一直角边和一锐角;b.斜边和一 锐角. 在Rt△ABC中,如果已知其中两边的长,你能求出 这个三角形的其他元 素吗? 1 应用勾股定理求斜边, 应用角的正切值求出 一锐角,再利用直角 三角形的两锐角互余, 求出另一锐角.一般 不用正弦或余弦值求 锐角,因为斜边是一 个中间量,如果是近 似值,会影响结果的 精确度. 已知斜边和直角边: 先利用勾股定理求出 另一直角边,再求一 锐角的正弦和余弦值, 即可求出一锐角,再 利用直角三角形的两 锐角互余,求出另一 锐角. 已知两直角边: 已知斜边和直角边: 例1 如图,在 Rt△ABC 中,∠C=90°,AC= ,BC= ,解这个直角三角形. 2 6 提问 需求的未知元素: 斜边AB、锐角A、锐角B. 方法一: 6tan = 3 2 60 =90 60 =30 =2 =2 2. BCA ,AC A B AB AC ∵ ∴∠ , ∠ , 方法二: 由勾股定理可得AB= .22. 3sin 60 90 30 2 , BCA , A B A . AB 例2 已知在Rt△ABC中,∠C=90°,∠A,∠B,∠C 的对边分别为a,b,c,且c=5,b=4,求这个三角 形的其他元素.(角度精确到1′) 求这个直角三角形的其他元素,与“解这个直角三角 形”的含义相同.求角时,可以先求∠A,也可以先 求∠B,因为 =sin B=cos A. 导引: b c 由c=5,b=4,得sin B= =0.8, ∴∠B≈53°8′. ∴∠A=90°-∠B≈36°52′. 由勾股定理得 解: 4 5 b c 2 2 2 25 4 3.a c b 已知直角三角形的一边和一锐角,解直角三角 形时,若已知一直角边a和一锐角A: ① ∠B=90 °- ∠ A;②c= 若已知斜边c和一个锐角A: ① ∠ B=90°- ∠ A; ②a=c·sin A ; ③b=c·cos A. . sin t ; an ab A a A ③ 2 例4 如图,在 Rt△ABC中,∠C=90°,∠B= 35°,b=20,解这个直角三角形(结果保留小数 点后一位). 提问 需求的未知元素: 直角边a、斜边c、锐角A. =90 =90 35 55 tan 20 28 6tan tan35 sin 20 34 9sin sin35 A B . bB ,a ba . .B bB ,c bc . .B 解: ∵ ∴ ∵ ∴ 还有别的 解法吗? 在直角三角形的6个元素中,直角是已知元素,如果 再知道一条边和第三 个元素,那么这个三角形的所有元 素就都可以确定下来. 例5 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分 别为a,b,c,且c=100,∠A=26°44′.求这个三角形 的其他元素.(长度精确到0.01) 已知∠A,可根据∠B=90°-∠A得到∠B的大小.而 已知斜边,必然要用到正弦或余弦函数. ∵∠A=26°44′,∠C=90°, ∴∠B=90°-26°44′=63°16′. 由sin A= 得a=c·sin A=100·sin 26°44′≈44.98. 由cos A= 得b=c·cos A=100·cos 26°44′≈89.31.,b c 解: 导引: ,a c 例6 如图,在△ABC中,AB=1,AC= sin B= 求BC的长. 要求的BC边不在直角 三角形中,已知条件中 有∠B的正弦值,作BC边上的高, 将∠B置于直角三角形 中,利用解直角三角形就可 解决问题. 2, 2 4 , 导引: 3 如图,过点A作AD⊥BC于点D. ∵AB=1,sin B= ∴AD=AB·sin B=1× = ∴BD= CD= ∴BC= 解: 2 4 , 2 4 2 . 4 2 2 2 2 2 141 , 4 4 AB AD 2 2 2 2 2 302 . 4 4 AC AD 30 14 30 14 . 4 4 4 CD BD 通过作垂线(高),将斜三角形分割成两个直角三角 形,然后利用解直角三角形来解决边或角的问题,这种 “化斜为直”的思想很常见.在作垂线时,要结合已知 条件,充分利用已知条件,如本题若过B点作AC的垂线, 则∠B的正弦值就无法利用. 1.已知在Rt△ABC中,∠C=90°. (1)若a= ,b= ,则c= ; (2)若a=10,c= ,则∠B= ; (3)若b=35,∠A=45°,则a= ; (4)若c=20,∠A=60°,则a= . 4 3 2 3 10 2 45° 2 15 35 10 3 随堂练习 2.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上, 且△ABD是等边三角形.若AB=2,求△ABC的周长. (结果保留根号) 解:∵△ABD是等边三角形,∴∠B=60°. 在Rt△ABC中,AB=2,∠B=60°, 2 4 tan 2 31cos 2 ABBC AC AB B . B g, △ABC的周长为2+ +4=6+2 3 2 3. 3.在Rt△ABC中,∠C=90°,tanA= ,△ABC 的周长为45cm,CD是斜边AB上的高,求CD的长.(精 确到0.1 cm) 12 5 5x 12x 13x 解: 5 15 1245 (cm) sin = 5 12 13 2 13 xAC A . x x x , 5x 12x 13x 15 12sin 6 9 cm 2 13 CD AC A . g ( ). 解 直 角 三 角 形 由直角三角形中已知的元素求出未知元 素的过程,叫作解直角三角形. 两边:两直角边或斜边、一直角边 一边一角:直角边、一锐角或斜边、一 锐角查看更多