江苏省徐州市2020届高三下学期春季联考数学试题 Word版含解析

江苏省徐州市2020届高三下学期春季联考数学试题 Word版含解析

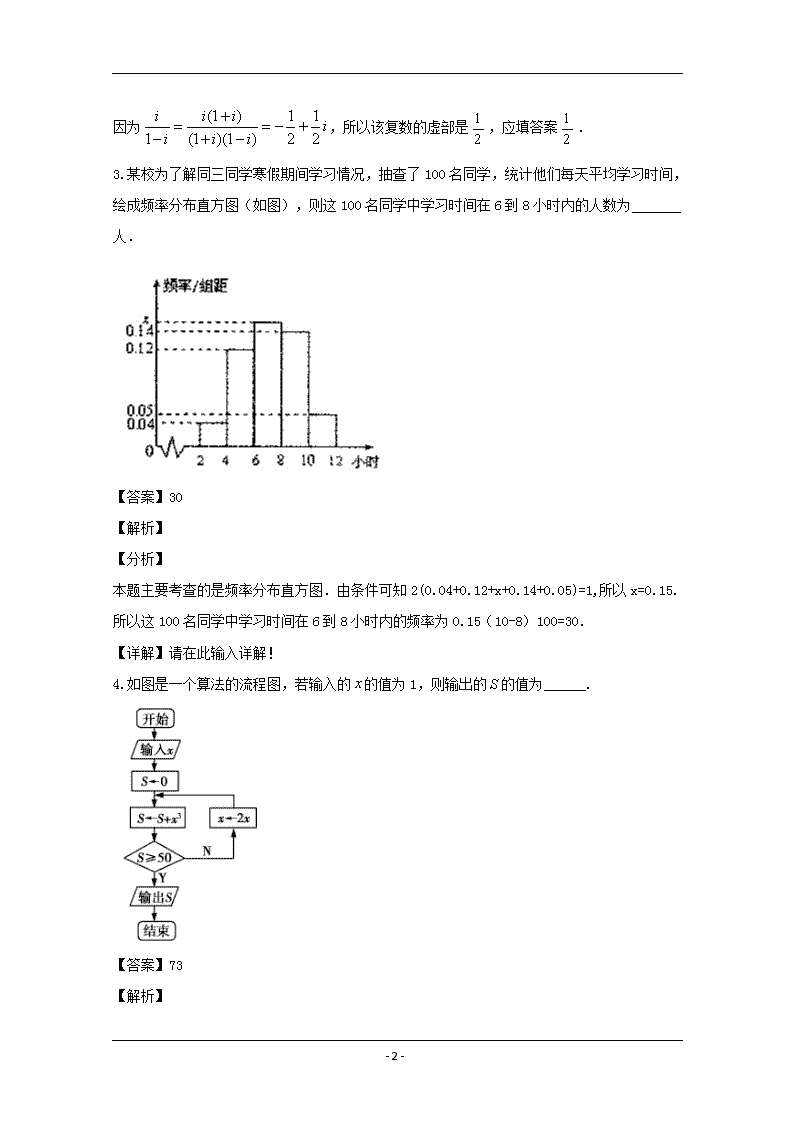
- 1 - 2020 届高三春季联考 数学Ⅰ 注意事项： 考生在答题前请认真阅读本注意事项及各题答题要求 1. 本试卷共 4 页，包含填空题（第 1 题~第 14 题）、解答题（第 15 题~第 20 题）两部分.本 卷满分为 160 分，考试时间为 120 分钟.考试结束后，请将本试卷和答题卡一并交回. 2. 答题前，请您务必将自己的姓名、考试证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答 题卡的规定位置. 3. 作答试题必须用 0.5 毫米黑色墨水的签字笔在答题卡的指定位置作答，在其它位置作答一 律无效.如需作图，须用 2B 铅笔绘图、写清楚，线条、符号等须加黑、加粗. 一、填空题：本大题共 14 小题，每小题 5 分，共计 70 分.请把答案填写在答题卡相应位置．．．．．．．上. 1.设全集U  R ，集合  1,0,1,2,3A   ，  | 2B x x  ，则 UA C B  __． 【答案】 1,0,1 【解析】 【分析】 直接根据交集和补集的定义求解，先求 UC B ，再求 UA C B ． 【详解】解：∵全集U  R ，集合  | 2B x x  ， ∴    | 2 ,2UC B x x    ， 又  1,0,1,2,3A   ， ∴  1,0,1UA C B   ， 故答案为： 1,0,1 ． 【点睛】本题主要考查集合的交集和补集运算，属于基础题． 2.复数 1 i i 的虚部是____________． 【答案】 1 2 【解析】 因为 (1 ) 1 1 1 (1 )(1 ) 2 2 i i i ii i i       ，所以该复数的虚部是 1 2 ，应填答案 1 2 ． - 2 - 3.某校为了解同三同学寒假期间学习情况，抽查了 100 名同学，统计他们每天平均学习时间， 绘成频率分布直方图（如图），则这 100 名同学中学习时间在 6 到 8 小时内的人数为 人． 【答案】30 【解析】 【分析】 本题主要考查的是频率分布直方图．由条件可知 2(0.04+0.12+x+0.14+0.05)=1,所以 x=0.15. 所以这 100 名同学中学习时间在 6 到 8 小时内的频率为 0.15（10-8）100=30． 【详解】请在此输入详解！ 4.如图是一个算法的流程图，若输入的 x 的值为 1，则输出的 S 的值为______. 【答案】73 【解析】 【分析】 根据循环结构逐步计算即可. - 3 - 【详解】输入 1x  , 0S  . 1. 30 1 1S    , 50S  判断为“ N ”, 2 1 2x    . 2. 31 2 9S    , 50S  判断为“ N ”, 2 2 4x    . 3. 39 4 73S    , 50S  判断为“Y ”. 输出 73S  . 故答案为： 73 【点睛】本题主要考查了根据输入数据计算循环框图的输出结果.属于基础题. 5.某校有 A ，B 两个学生食堂，若 a ，b ，c 三名学生各自随机选择其中的一个食堂用餐，则 三人不在同一个食堂用餐的概率为______. 【答案】 3 4 【解析】 【分析】 求出所有可能的情况总数,进而求得在同一食堂用餐的概率,再利用对立事件的概率公式求解 三人不在同一个食堂用餐的概率即可. 【详解】由题意可知,所有可能的情况共有 32 8 种,其中在同一食堂用餐的情况有 2 种.故三 人不在同一个食堂用餐的概率为 2 31 8 4   . 故答案为： 3 4 【点睛】本题主要考查了古典概型的问题,需要根据题意求出所有可能的情况,再求出对立事 件的概率进行计算.属于基础题. 6.已知正四棱锥的底面边长是 4 2 ，侧棱长为 5，则该正四棱锥的体积为______. 【答案】32 【解析】 【分析】 连接底面对角线交于O ,再根据四棱锥的性质求出高即可求得体积. 【详解】设正四棱锥为 S ABCD ,连接 ,AC BD 交于 O ,连接 SO .易得 SO  平面 ABCD . - 4 - 根据正四棱锥的性质有 4BO  , 2 25 4 3SO    . 故该正四棱锥的体积为  21 4 2 3 323V     . 故答案为：32 【点睛】本题主要考查了正四棱锥体积的计算,需要根据其中的直角三角形进行高的计算.属 于基础题. 7.若将函数   sin 2 3f x x      的图象沿 x 轴向右平移  0   个单位后所得的图象关于 y 轴对称，则 的最小值为______. 【答案】 5 12  【解析】 【分析】 先根据求解平移后的函数解析式,再根据三角函数对称轴的性质求解即可. 【详解】 将函数   sin 2 3f x x      的图象沿 x 轴向右平 移  0   个单位后 可得   sin 2 2 3g x x       . 由题  g x 关于 y 轴对称,故当 0x  时，有  2 ,3 2 k k Z       , 即  ,2 12 k k Z     .因为 0  ，故当 1k   时有 的最小值为 5 12  . 故答案为： 5 12  【点睛】本题主要考查了三角函数图像平移以及三角函数图像性质的问题,需要根据题意代入 对称轴表达式进行求解.属于基础题. 8.已知 na 为等差数列，其公差为 2，且 7a 是 3a 与 9a 的等比中项， nS 为 na 前 n 项和，则 10S - 5 - 的值为______. 【答案】-110 【解析】 【分析】 利用基本量法以及等比中项的性质可求得首项 1 20a  ,再求解 10S 即可. 【详解】因为 7a 是 3a 与 9a 的等比中项,故 37 2 9aa a  ,即     1 1 1 26 2 8a a ad d d     , 即 2 2 1 1 2 1 1 212 36 10 16a a a ad d d d     , 化 简 得  1 10 0ad d  . 又 2d  所 以 1 20a  . 故  10 10 910 20 2 1102S        . 故答案为： 110 【点睛】本题主要考查了等差数列中基本量的求解以及等比中项的运用,同时也考查了等差数 列求和的公式.属于中档题. 9.若双曲线 2 2 2 2 1x y a b   的一条渐近线与圆C ： 2 21 1x y   相交于 A ， B 两点且 90ACB  ，则此双曲线的离心率为______. 【答案】 2 【解析】 【分析】 根据圆的半径相等以及 90ACB   可求得圆心  1,0 到渐近线的距离为 2 2 ,再利用点到线 的距离公式列式求解 ,a b 的关系,再求解离心率即可. 【详解】因为 90ACB  , 1AC BC  ,故圆心 1,0 到渐近线的距离为 2 22 AC  . 不妨设渐近线方程为 by xa  ,即 0bx ay  .故 2 2 2 2 b b ca b    ,即 2c b . 所以  2 2 2 22 2c b c a   .故 2 22c a ,故双曲线的离心率为 2c a  . 故答案为： 2 - 6 - 【点睛】本题主要考查了直线与圆的位置关系以及建立齐次式求解双曲线离心率的问题.属于 基础题. 10.函数 2 3 4( ) lg( 1) x xf x x     的定义域为__________． 【答案】   1,0 0,1  ； 【解析】 2 4 1 3 4 0{ { 1 1 1 0 lg( 1) 0 0 x x x x x x x x                   且 ，即定义域为   1,0 0,1  11.已知 ,x y R ，且 1x  ，若  1 2 1x y   ，则 6 6xy x y   的最小值为______. 【答案】25 【解析】 【分析】 由题意   6 6 1 6xy x y x y      ,再根据  1 2 1x y   换元令 1, 2a x b y    , 代入   1 6x y  展开利用基本不等式求最小值即可. 【详解】由题,   6 6 1 6xy x y x y      ,设 1, 2a x b y    则 1ab  .      1 6 2 8 8 2 16 17 2 8 2 17 8 25x y a b ab a b a b               . 当且仅当8 2a b 时取等号. 故答案为： 25 【点睛】本题主要考查了换元法利用基本不等式求解最小值的问题.需要根据题中所给的形式 换元,结合基本不等式求最小值.属于中档题. 12.在 ABC 中，若 120BAC   ， 2BA  ， 3BC  ， 1 1 3 2BM BC BA    ，则 MA MC   ______. 【答案】 6 3 2  【解析】 【分析】 - 7 - 利用余弦定理可求得 6 1AC   ,建立平面直角坐标系,根据 1 1 3 2BM BC BA    求出 M 的坐标,进而求得 MA MC  即可. 【详解】由余弦定理可得 2 2 2 2 cos120BC AB AC AB AC      ,即 2 2 5 0AC AC   , 因为 0AC  ,故解得 6 1AC   . 过 B 作 BO 垂直 AC 的延长线于O ,再以O 为坐标原点,OC  为 x 轴, OB  为 y 轴建立平面直 角坐标系.则  06,C ,  0, 3B , ( )1,0A . 设  ,M x y ,因为 1 1 3 2BM BC BA    ,故     1 1, 3 6, 3 1, 33 2x y      , 故 6 1 3 2 3 33 3 2 x y         ,解得 6 1 3 2 3 6 x y      ,即 6 1 3 3 2 6,M      . 故 1 6 3 2 6 1 3 6 1 4 6 1 2 3 6 3 2 6 3 4 3 6 1 6 3, , 22MA MC                           故答案为： 6 3 2  【点睛】本题主要考查了建立平面直角坐标系求解向量数量积的问题.需要根据题意建立合适 的坐标系,再根据题中所给的数据进行向量坐标的运算.属于中档题. 13.已知圆 2 2 : 4O x y  ，直线l 与圆O 交于 P Q， 两点，  2,2A ，若 2 2 40AP AQ  ， 则弦 PQ 的长度的最大值为___________. 【答案】 2 2 - 8 - 【解析】 【分析】 取 PQ 的中点为 M，由 2 2 40AP AQ  可得 2 2 16AM OM  ，可得 M 在 2 0x y   上， 当OM 最小时，弦 PQ 的长才最大. 【 详 解 】 设 M 为 PQ 的 中 点 ，  2 2 2 22 (2 )AP AQ AM PQ   ， 即 2 2 2 22 2AP AQ AM MQ   ， 即  2 2 240 2 2AM OQ OM   ， 2 220 4AM OM   ， 2 2 16AM OM  . 设  ,M x y ，则  2 2 2 2( 2) ( 2) 16x y x y      ，得 2 0x y   . 所以 min 2 2 2 OM   ， max 2 2PQ  . 故答案为： 2 2 【点睛】本题考查直线与圆的位置关系的综合应用，考查学生的逻辑推理、数形结合的思想， 是一道有一定难度的题. 14.函数  f x 满足    4f x f x  ，当  2,2x  时， 3 22 3 , 2( ) 1 , 2 x x a x af x x a x           ， 若函数  f x 在 0,2020 上有 1515 个零点，则实数 a 的范围为___________. 【答案】 1 ,02     【解析】 【分析】 由已知，  f x 在[ 2,2) 上有 3 个根，分 2 1a  ，0 1a  ， 1 0a   ， 2 1a    四 - 9 - 种情况讨论  f x 的单调性、最值即可得到答案. 【详解】由已知，  f x 的周期为 4，且至多在[ 2,2) 上有 4 个根，而 0,2020 含 505 个周期， 所以  f x 在[ 2,2) 上有 3 个根，设 3 2( ) 2 3g x x x a   ， ' 2( ) 6 6g x x x  ，易知 ( )g x 在 ( 1,0) 上 单 调 递 减 ， 在 ( , 1)  ， (1, ) 上 单 调 递 增 ， 又 ( 2) 4 0g a    ， (1) 5 0g a   . 若 2 1a  时，  f x 在 ( ,2)a 上无根，  f x 在[ 2, ]a 必有 3 个根， 则 ( 1) 0 (0) 0 f f     ，即 1 0 0 a a     ，此时 a ； 若 0 1a  时，  f x 在 ( ,2)a 上有 1 个根，注意到 (0) 0f a  ，此时  f x 在[ 2, ]a 不可 能有 2 个根，故不满足； 若 1 0a   时，要使  f x 在[ 2, ]a 有 2 个根，只需 ( 1) 0 ( ) 0 f f a     ，解得 1 02 a   ； 若 2 1a    时，  f x 在[ 2, ]a 上单调递增，最多只有 1 个零点，不满足题意； 综上，实数 a 的范围为 1 02 a   . 故答案为： 1 ,02     【点睛】本题考查利用导数研究函数的零点个数问题，涉及到函数的周期性、分类讨论函数 的零点，是一道中档题. 二、解答题：本大题共 6 小题，共计 90 分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字 说明、证明过程或演算步骤. 15.已知向量  cos ,sinm x x ，  3sin ,sinn x x ，函数  f x m n   . （1）求函数  f x 的最小正周期. （2）若 0, 2      ， 13 2 10f      ，求sin 的值. 【答案】（1） ；（2） 4 3 3 10  . - 10 - 【解析】 【分析】 (1) 根 据 平 面 向 量 的 数 量 积 公 式 以 及 降 幂 公 式 与 辅 助 角 公 式 化 简 可 得   1sin 2 6 2f x x       ,进而求得最小正周期. (2)代入 13 2 10f      可得 4sin 6 5      ,再根据sin sin 6 6            ,利用三角函 数和差角公式以及同角三角函数关系求解即可. 【详解】（1） 2( ) 3sin cos sinf x x x x  3 1 cos 1sin 2 sin 22 2 6 2 xx x          , ∴  f x 的最小正周期为 . （2） 1 13sin2 6 2 10f               ,∴ 4sin 6 5      , ∵ 0 2   ,∴ 6 6 3       , ∴ 2 2 4 3cos 1 sin 16 6 5 5                         , ∴sin sin sin cos cos sin6 6 6 6 6 6                                   4 3 3 1 5 2 5 2 4 3 3 10      . 【点睛】本题主要考查了同角三角函数公式以及三角函数的恒等变换.同时也考查了根据三角 函数值求三角函数值的问题.属于中档题. 16.如图，在直三棱柱 1 1 1ABC A B C 中， AC BC ， M 是棱 1CC 上的一点. - 11 - （1）求证： BC AM ； （2）若 M ， N 分别是 1CC ， AB 的中点，求证： / /CN 平面 1AMB . 【答案】（1）证明见解析；（2）证明见解析. 【解析】 【分析】 (1)根据直三棱柱的性质证明 BC ⊥平面 1 1ACC A 即可. (2) 取 1AB 的中点为Q ,连接 NQ ,QM ,再证四边形 NCMQ 为平行四边形即可. 【详解】（1）在直三棱柱 1 1 1ABC A B C 中, 1CC  平面 ABC , BC 平面 ABC ,∴ 1CC BC , 又∵ BC AC , 1AC CC C , AC  平面 1 1ACC A , 1CC  平面 1 1ACC A , ∴ BC ⊥平面 1 1ACC A , 又∵ AM  平面 1 1ACC A ,∴ BC AM . （2）取 1AB 的中点为Q ,连接 NQ , QM , ∵在 1ABB△ 中, N 、Q 分别为 AB 、 1AB 中点,∴ 1/ /NQ AB 且 1 1 2NQ AB , 在直三棱柱 1 1 1ABC A B C 中, ∵ 1 1/ /BB CC 且 1 1BB CC , M 为 1CC 的中点,∴ 1/ /CM BB 且 1 1 2CM BB , ∴ / /NQ MC 且 NQ MC ,∴四边形 NCMQ 为平行四边形,∴ / /NC QM , 又∵ NC  平面 1AMB ,QM  平面 1AMB ,∴ / /CN 平面 1AMB . - 12 - 【点睛】本题主要考查了线面垂直以及线面平行的证明.属于基础题. 17.如图，某居民区内有一直角梯形区域 ABCD ， / /AB CD ， AB BC ， 6AB  百米， 4CD  百米.该区域内原有道路 AC ，现新修一条直道 DP（宽度忽略不计），点 P 在道路 AC 上（异于 A ，C 两点）， 6BAC   ， DPA   . （1）用 表示直道 DP 的长度； （2）计划在 ADP△ 区域内修建健身广场，在 CDP 区域内种植花草.已知修建健身广场的成 本为每平方百米 4 万元，种植花草的成本为每平方百米 2 万元，新建道路 DP 的成本为每百米 4 万元，求以上三项费用总和的最小值（单位：万元）. 【答案】（1） 2 sinDP  ， 5 6 6    .（2）16 3 万元. 【解析】 【分析】 (1) 过点 D 作 'DD 垂直于线段 AB ,垂足为 'D 得到 6DAP   ,再在 ADP△ 中,由正弦定理 求得 DP 即可. (2) 在 ADP△ 中,由正弦定理求得 AP ,进而根据 DPC ADC APDS S S △ △ △ 求出 DPCS△ ,再根据 题意表达出总费用 2 cos( ) 12 3 4 sinf         ,再求导分析 ( )f  的单调性与最值即可. - 13 - 【详解】（1）过点 D 作 'DD 垂直于线段 AB ,垂足为 'D . 在直角 ABC 中,因为 AB BC , 6BAC   , 6AB  ,所以 2 3BC  . 在直角 'ADD△ 中,因为 ' 2AD  , ' 2 3DD  ,所以 4AD ,则 3sin ' 2DAD  , 故 ' 3DAD   , 又 6BAC   ,所以 6DAP   . 在 ADP△ 中,由正弦定理得 sin sin 6 AD DP   , 所以 2 sinDP  , 5 6 6    . （2）在 ADP△ 中,由正弦定理得 sin sin AP AD ADP  , 所以 54sin4sin 6 sin sin ADPAP           . 所以 54sin1 1 26sin sin2 2 sin sinAPDS AP PD               △ 54sin 6 sin        . 又 1 1 2sin 4 4sin 4 32 2 3ADC AD DC ADCS        △ . 所以 54sin 64 3 sinDPC ADC APDS S S         △ △ △ . 设三项费用总和为  f  , - 14 - 则 5 54sin 4sin 26 6( ) 4 4 3 2 4sin sin sinf                                2 cos12 3 4 sin         , 5 6 6    , 所以 2 1 cos2'( ) 8 sinf              ,令  ' 0f   ,则 2 3   . 列表：  2,6 3       2 3  2 5,3 6       'f  - 0 +  f  单调递减 2 3 单调递增 所以 2 3   时,   min 16 3f     . 答：以上三项费用总和的最小值为16 3 万元. 【点睛】本题主要考查了解三角形在实际中的运用,同时也考查了利用导数求解实际运用中的 最值问题,需要根据题意确定函数与自变量的角度间的关系,再求导分析单调性以及最值等. 属于难题. 18.在平面直角坐标系 xOy 中，已知椭圆C ：   2 2 2 2 1 0x y a ba b     过点 0,1 ，椭圆C 的 离心率为 3 2e  . - 15 - （1）求椭圆C 的标准方程； （2）如图，设直线 l 与圆  2 2 2 1 2x y r r    相切与点 A ，与椭圆C 相切于点 B ，当 r 为 何值时，线段 AB 长度最大？并求出最大值. 【答案】（1） 2 2 14 x y  ；（2） 2R  时， AB 最大值为 1. 【解析】 【分析】 (1)利用基本量 , ,a b c 的关系列式求解即可. (2) 设直线l 的方程为 y kx m  ,根据直线 l 与圆C 相切可得  2 2 21m R k  ,再联立直线 与椭圆的方程,利用相切则所得的二次方程判别式为 0 可得 2 24 1 0k m   ,再联立  2 2 21m R k  可得 2 2 2 2 2 2 3 4 1 4 Rm R Rk R       .再根据点的坐标结合距离公式以及 2 2 2AB OB OA  ,在根据基本不等式求解最大值即可. 【详解】解：（1）由题, 31, 2 cb a   , 故 2 2 2 3 4 a b a   ,解得 2 4a  . 故椭圆方程为 2 2 14 x y  . （2）连接 OA,OB，如图所示： - 16 - 设直线l 的方程为 y kx m  , 因为直线 l 与圆C ：  2 2 2 1 2x y R R    相切于 A , 所以 21 mR k   ,即  2 2 21m R k  ①, 因为 l 与椭圆 E ： 2 2 14 x y  相切于点 B , 由 2 2 14 y kx m x y     得 2 24( ) 4x kx m   , 即 2 2 21 4 8 4 4 0k x kmx m     有两个相等的实数解, 则     2 2 2 2 2 264 16 1 4 1 16 4 1 0k m k m k m         , 即 2 24 1 0k m   ,② 由①、②可得 2 2 2 2 2 2 3 4 1 4 Rm R Rk R       , 设  1 1,B x y ,由求根公式得  1 22 8 4 4 2 1 4 km km kx m mk        , ∴ 2 2 1 1 4 4 1k k my kx m k mm m m            , ∴ 2 2 2 2 2 1 1 2 16 1 45kx y m ROB      , ∴在直角三角形OAB 中, - 17 - 2 22 2 2 2 2 45 45AB OB OA R RRR            , 因为 2 2 4 4RR   ,当且仅当  2 1,2R   时取等号, 所以 2 5 4 1AB    , 即当  2 1,2R   时, AB 取得最大值,最大值为 1. 【点睛】本题主要考查了椭圆中基本量的求解,同时也考查了直线与圆和椭圆等相切时的方法. 当直线与圆相切时利用圆心到直线的距离等于半径列式,当直线与椭圆相切时联立方程根据 判别式为 0 列式.属于难题. 19.已知函数   lnf x x x a  和函数   lng x x ax  . （1）若曲线  f x 在 1x  处的切线过点  2, 2A  ，求实数 a 的值； （2）求函数     2h x g x x  的单调区间； （3）若不等式     0f x g x  对于任意的 1x  恒成立，求实数 a 的最大值. 【答案】（1） 3a   ；（2）当 2 2a  时,单调递增区间为 0,  ; 当 2 2a  时,单调增区间为 2 80, 4 a a      ， 2 8 ,4 a a       ，单调递减区间为 2 28 8,4 4 a a a a        ；（3）2. 【解析】 【分析】 (1)根据导数的几何意义求解即可. (2)易得   2lnh x x ax x   ,再求导分析导函数分子 22 1y x ax   的根的存在情况,进而 可得导函数在区间上的正负以及原函数的单调性. (3)令       ln lnF x f x g x x x x ax a      ,再求导分析可得  'F x 在  1, 上单调 递增,可得    ' ' 1 2F x F a   .再分 2a  与 2a  两种情况分析函数的单调性求解最小值 即可. 【详解】解（1）∵  ' ln 1f x x  ,∴  ' 1 1f  ,又∵  1f a , - 18 - 曲线  f x 在 1x  处的切线方程为 1y a x   , ∵切线过点  2, 2A  ,∴ 2 2 1a    ,∴ 3a   . （2）   2lnh x x ax x   的定义域为 0,  ,   22 1' 0x axh x x    ,则 22 1 0x ax   ,令 2 8a   . （Ⅰ）当 2 8 0a    即 2 2 2 2a   时  ' 0h x  , ∴函数  h x 的单调增区间为： 0,  . （Ⅱ）当 2 8 0a    即 2 2a   或 2 2a  时, 22 1 0x ax   有两个不等的实数根 2 1 8 4 a ax   , 2 2 8 4 a ax   , 当 2 2a   时, 1 0x  , 2 0x  ,∴  ' 0h x  , 函数  h x 单调增区间为  0,  , 当 2 2a  时, 1 > 0x , 2 0x  , 令  ' 0h x  ,则 10 x x  或 2x x , 令  ' 0h x  ,则 1 2x x x  , ∴  h x 单调递增区间为 2 80, 4 a a      , 2 8 ,4 a a       ,  h x 单调递减区间为 2 28 8,4 4 a a a a        . 综上所述, 当 2 2a  时,单调递增区间为 0,  ; 当 2 2a  时,单调增区间为 2 80, 4 a a      ， 2 8 ,4 a a       ，单调递减区间为 2 28 8,4 4 a a a a        ； （3）令       ln lnF x f x g x x x x ax a      , - 19 - 则   1' ln 1F x x ax     , 记   1ln 1x axx     ,则   2 2 1 1 0' 1 xx x x x      ,所以  'F x 在  1, 上单调递增, 故    ' ' 1 2F x F a   , 当 2a  ,  ' 0F x  ,故  F x 在  1, 上单调递增, 所以    1 0F x F  ,符合题意. 当 2a  时,   1' 1 0  a aF e e ,故  ' '(1) 0aF e F  , 又  'F x 在  1, 上单调递增,所以存在唯一的实数  0 1,x   ,使得  0' 0F x  , 列表如下： x  01, x 0x  0,x   'F x - 0 +  F x  极小值  则当  01,x x 时,    1 0F x F  ,这与   0F x  恒成立矛盾. 综上,实数 a 的最大值为 2. 【点睛】本题主要考查了导数的几何意义以及利用导数分析含参函数的单调性问题.同时也考 查了利用导数解决恒成立的问题.需要根据题意分析导数的零点存在性以及大小关系,进而确 定函数的单调性以及最值.属于难题. 20.已知等差数列 na 和等比数列 nb 的各项均为整数，它们的前 n 项和分别为 ,n nS T ，且 1 12 2b a  ， 2 3 2 254, 11b S a T   . （1）求数列 na ， nb 的通项公式； （2）求 1 1 2 2 3 3n n nM a b a b a b a b     ； （3）是否存在正整数 m ，使得 1m m m m S T S T   恰好是数列 na 或 nb 中的项？若存在，求出所有 - 20 - 满足条件的 m 的值；若不存在，说明理由. 【答案】（1） 12 1, 2 3n n na n b     ；（2） 2( 1) 3 2n nM n    ；（3）存在，1. 【解析】 【分析】 （1）利用基本量法直接计算即可； （2）利用错位相减法计算； （3） 2 1 *1 2 1 3 1 3 m m m m m m S T m NS T m        ，令 2 1 * 2 1 3 ,1 3 m m m L L Nm      可得  2( 1) 1 (3 )3mL m L    ，1 3L „ ，讨论即可. 【详解】（1）设数列 na 的公差为 d ，数列 nb 的公比为 q， 因为 1 1 2 3 2 22 2, 54, 11b a b S a T     ， 所以 2 (3 3 ) 54 1 2 2 11 q d d q        ，即 (1 ) 9 2 8 q d d q      ，解得 3 2 q d    ，或 3 2 5 q d     （舍去）. 所以 12 1, 2 3n n na n b     . （2）  2 1 1 1 2 2 3 3 1 2 3 2 3 5 2 3 2 1 2 3n n n nM a b a b a b a b n                   ， 2 13 1 2 3 3 2 3 (2 3) 2 3 (2 1) 2 3n n nM n n               ， 所以  2 12 2 4 3 3 3 (2 1) 2 3n n nM n          ， 13(1 3 )2 4 (4 2) 3 4 (4 4) 31 3 n n nn n            所以 2( 1) 3 2n nM n    . （3）由（1）可得 2 nS n ， 3 1 n nT ， 所以 2 1 1 2 1 3 1 3 m m m m m m S T m S T m       . 因为 1m m m m S T S T   是数列 na 或 nb 中的一项，所以 2 1 * 2 1 3 ,1 3 m m m L L Nm      ， 所以  2( 1) 1 (3 )3mL m L    ，因为 2 1 0,3 0mm  … ， - 21 - 所以1 3L „ ，又 *L N ，则 2L  或 3L  . 当 2L  时，有  2 1 3mm   ，即  2 1 13m m   ，令 2 1( ) 3m mf m  . 则 2 2 2 1 1 ( 1) 1 1 2 2 3( 1) ( ) 3 3 3m m m m m m mf m f m             . 当 1m  时， (1) (2)f f ；当 2m  时，    1 0f m f m   ， 即 (1) (2) (3) (4)f f f f     . 由 1(1) 0, (2) 3f f  ，知  2 1 13m m   无整数解. 当 3L  时,有 2 1 0m   ，即存在 1m  使得 2 1 2 1 3 31 3 m m m m     是数列 na 中的第 2 项， 故存在正整数 1m  ，使得 1m m m m S T S T   是数列 na 中的项. 【点睛】本题考查数列的综合应用，涉及到等差、等比数列的通项，错位相减法求数列的前 n 项和，数列中的存在性问题，是一道较为综合的题. 2020 届高三春季联考 数学Ⅱ（附加题） 注意事项： 考生在答题前请认真阅读本注意事项及各题答题要求： 1. 本试卷共 2 页，均为非选择题（第 21 题~第 23 题）.本卷满分为 40 分.考试时间为 30 分 钟.考试结束后，请将本试卷和答题卡一并交回. 2. 答题前，请您务必将自己的姓名、考试证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答 题卡的规定位置. 3. 作答试题必须用 0.5 毫米黑色墨水的签字笔在答题卡的指定位置作答，在其它位置作答一 律无效.如需作图，须用 2B 铅笔绘、写清楚，线条、符号等须加黑、加粗. 21.【选做题】本题包括 A，B，C 三小题，请选定其中两题，并在答题卡相应的区域内作答. 若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A.【选修 4-2：矩阵与变换】 21.已知二阶矩阵 1 3 aM b      的特征值是 1   所对应的一个特征向量 1 1 3e       . （1）求矩阵 M ； - 22 - （2）设曲线C 在变换矩阵 M 作用下得到的曲线 'C 的方程为 1xy  ，求曲线C 的方程. 【答案】（1） 2 1 3 0M      ；（2） 26 3 1x xy  【解析】 【分析】 (1)根据特征值与特征向量的性质计算即可. (2) 曲线C 上一点  ,P x y 在矩阵 M 的作用下的到点  ' ', 'P x y ,进而求得 ' 2 ' 3 x x y y x     ,再 代入 1xy  化简即可. 【详解】解：（1）由 1 1 113 3 3 a b                    得 3 1 3 3 3 a b       ,即 2 0 a b    , ∴ 2 1 3 0M      . （2）设曲线C 上一点  ,P x y 在矩阵 M 的作用下的到点  ' ', 'P x y ,则点 P' 在曲线 'C 上. ∴ 2 1 ' 3 0 ' x x y y                 ,即 ' 2 ' 3 x x y y x     , 又∵ ' ' 1x y  ,∴ 2 3 1x y x   , 整理得曲线C 的方程为 26 3 1x xy  . 【点睛】本题主要考查了特征值与特征向量的运用,同时也考查了矩阵变换的运用,属于基础 题. B.【选修 4-4：坐标系与参数方程】 22.已知极坐标系的极点与直角坐标系的原点重合，极轴与 x 轴的正半轴重合.若直线l 的极坐 标方程为 sin 3 24       . （1）把直线 l 的极坐标方程化为直角坐标方程； （2）已知 P 为椭圆C ： 2 2 13 x y  上一点，求 P 到直线l 的距离的最小值. 【答案】（1） 6 0x y   ；（2） 2 2 - 23 - 【解析】 【分析】 (1)根据三角函数公式以及极坐标与直角坐标的互化求解即可. (2) 设  3 cos ,sinP   ,再求出点到线的距离表达式,利用三角函数性质求解最值即可. 【详解】解：（1）直线 l 的极坐标方程 sin 3 24       ,则 2 2sin cos 3 22 2      , 即 sin cos 6     , 所以直线 l 的直角坐标方程为 6 0x y   ； （2） P 为椭圆C ： 2 2 13 x y  上一点,设  3 cos ,sinP   ,其中  0,2  , 则 P 到直线l 的距离 2cos 663 cos sin 6 2 2 d            , ∴当 cos 16       时, d 的最小值为 2 2 . 【点睛】本题主要考查了直角坐标和极坐标的互化,同时也考查了利用参数方程求解点到线的 距离最值问题.属于中档题. C.【选修 4-5：不等式选讲】 23.已知实数 , ,x y z 满足 2x y z   ，求 2 2 22 3x y z  的最小值. 【答案】 24 11 【解析】 【分析】 由柯西不等式知：（x+y+z）2≤[（ 2 x）2+（ 3 y）2+z2]•[（ 1 2 ）2+（ 1 3 ）2+12]故 2x2+3y2+z2 24 11  ， 由此能求出 2x2+3y2+z2 的最小值． 【详解】由柯西不等式可知： - 24 - （x+y+z）2≤[（ 2 x）2+（ 3 y）2+z2]•[（ 1 2 ）2+（ 1 3 ）2+12]， 故 2x2+3y2+z2 24 11  ， 当且仅当 2 3 1 1 1 2 3 x y z  ， 即：x 6 11  ，y 4 11  ，z 12 11  时， 2x2+3y2+z2 取得最小值为 24 11 ． 【点睛】本题考查柯西不等式的应用，考查了等号成立的条件，属于基础题． 【必做题】第 22 题、第 23 题，每题 10 分，共计 20 分.请在答卷纸指定区域内作答.解答应 写出文字说明、证明过程或演算步骤. 24.已知  1 1,A x y ，  2 2,B x y 是抛物线C ：  2 2 0x py p  上不同两点. （1）若抛物线C 的焦点为 F ，  0 0,D x y 为 AB 的中点，且 04 2AF BF y   ，求抛物线C 的方程； （2）若直线 AB 与 x 轴交于点 P ，与 y 轴的正半轴交点Q ，且 2 1 2 4 py y  ，是否存在直线 AB ， 使得 1 1 3 PA PB PQ   ？若存在，求出直线 AB 的方程；若不存在，请说明理由. 【答案】（1） 2 8x y ；（2）存在， AB ： 1 2 2 py x   【解析】 【分析】 (1)根据抛物线的定义求解即可. (2) 设 AB ：  0, 0y kx m k m    ,联立直线与抛物线的方程,再转换可得 3' ' OQ OQ AA BB   ,进而利用点坐标与韦达定理代入化简求解即可. 【详解】解：（1）由抛物线的定义得 1 2AF BF y y p    0 02 4 2y p y    ,∴ 4p  , - 25 - ∴所求抛物线方程为 2 8x y . （2）由题意得 AB 的斜率存在设 AB ：  0, 0y kx m k m    , 2 2 2 2 02 y kx m x pkx pmx py        ,∴ 1 2 2x x pk  , 1 2 2x x pm  , ∴ 2 2 1 2 4 py y m  ,∴ 2 pm  , 2 1 2 2 2y y pk m   , 作 'AA x 轴, 'BB x 轴,垂足为 'A , 'B , ∵ 1 1 3 PA PB PQ   ,∴ 3PQ PQ PA PB   ,∴ 3' ' OQ OQ AA BB   , ∴    2 1 2 2 1 2 1 2 2 2 4 m pk mm y ym m py y y y     2 2 2 122 2 31 44 p pk p k p      . ∴ 2 1 4k  ,∴ 1 2k   ,∴存在直线 AB ： 1 2 2 py x   符合题意. 【点睛】本题主要考查了抛物线的定义运用,同时也考查了联立直线与抛物线的方程,利用韦 达定理表达弦长进行化简求解的问题.属于中档题. 25.已知数集  1 2, , , nA a a a  ，其中 1 20 na a a    ，且 3n  ，若对  , 1i j i j n    ， j ia a 与 j ia a 两数中至少有一个属于 A ，则称数集 A 具有性质 P . （1）分别判断数集 0,1,3 与数集 0,2,4,6 是否具有性质 P ，说明理由； （2）已知数集  1 2 8, , ,A a a a  具有性质 P ，判断数列 1a ， 2a ，…， 8a 是否为等差数列， 若是等差数列，请证明；若不是，请说明理由. 【答案】（1）数集 0,1,3 不具有性质 P ，数集 0,2,4,6 具有性质 P ，理由见解析；（2）是 等差数列，证明见解析 【解析】 【分析】 (1)根据性质 P 的定义逐个求差判断即可. (2)根据性质 P 的定义可先判断出 1 0a  ,再判断可得  8 2,3, ,8ka a A k    ,继而得到  1 8 7 2,3, ,8i ia a a a i     即可证明数列 1a , 2a ,…, 8a 为等差数列. - 26 - 【详解】解：（1）由于 3 1 和 3 1 都不属于集合 0,1,3 , 所以该集合不具有性质 P ； 由于 2 0 、 4 0 、6 0 、 4 2 、 6 2 、6 4 、0 0 、 2 2 、 4 4 、 6 6 都属于集合  0,2,4,6 , 所以该数集具有性质 P . （2）∵  1 2 8, , ,A a a a  具有性质 P ,所以 8 8a a 与 8 8a a 中至少有一个属于 A , 由 1 2 80 a a a    ,有 8 8 8a a a  ,故 8 8a a A  ,∴ 8 80 a a A   ,故 1 0a  . ∵ 1 2 80 a a a    ,∴ 8 8ka a a  ,故  8 2,3, ,8ka a A k    . 由 A 具有性质 P 知,  8 2,3, ,8ka a A k    , 又∵ 8 8 8 7 8 2 8 1a a a a a a a a        , ∴ 8 8 1a a a  , 8 7 2a a a  ,…, 8 2 7a a a  , 8 1 8a a a  , 即  9 8 1,2, ,8i ia a a i    ①, 由 2 7 8a a a  知, 3 7a a , 4 7a a ,…, 7 7a a 均不属于 A , 由 A 具有性质 P , 7 3a a , 7 4a a ,…, 7 7a a 均属于 A , ∴ 7 7 7 6 7 4 7 3 8 3a a a a a a a a a a          ,而 8 3 6a a a  , ∴ 7 7 0a a  , 7 6 2a a a  , 7 5 3a a a  ,…, 7 3 5a a a  即  8 7 1,2, ,7i ia a a i    ②, 由①②可知   8 9 8 7 1 1,2, ,8i i ia a a aa ia       , 即  1 8 7 2,3, ,8i ia a a a i     . 故 1a , 2a ,…, 8a 构成等差数列. 【点睛】本题主要考查了数列与集合的新定义问题,需要根据所给的性质,先分析到最小的元 素,再推导出元素之间的关系,进而得到元素间的递推公式分析.属于难题. - 27 -