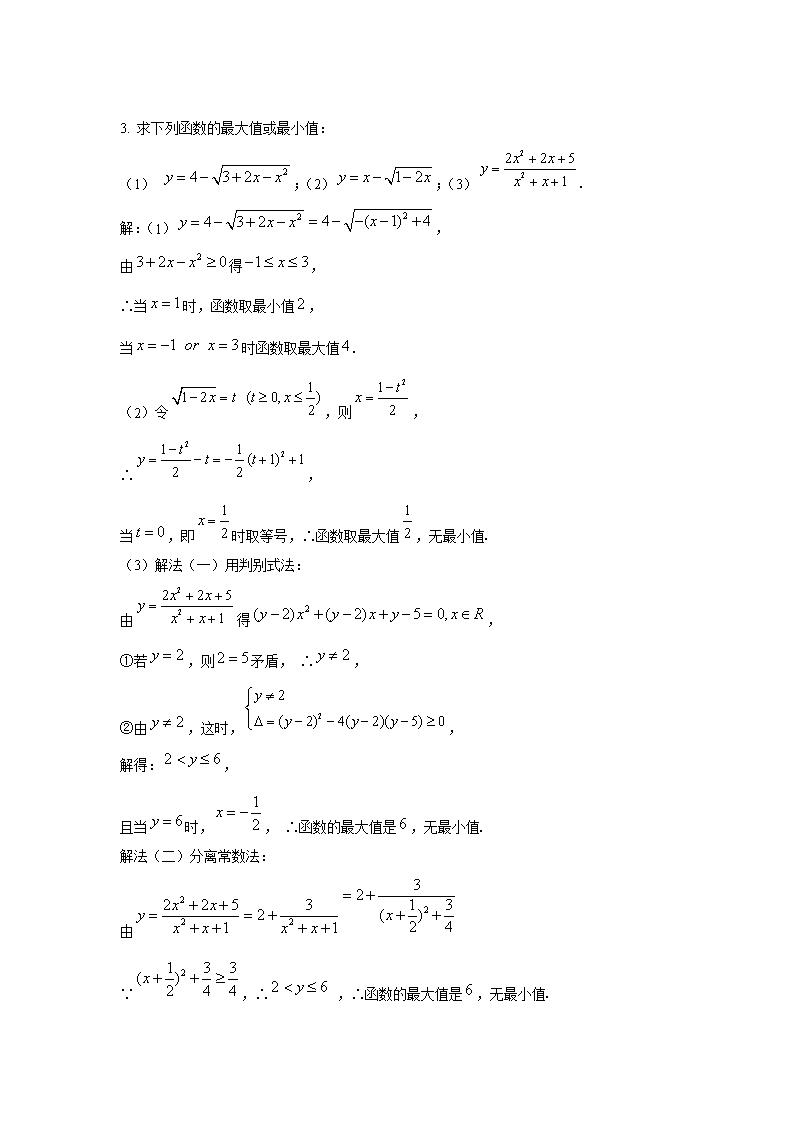一线名师指点高考同步辅导函数的定义域值域最大最小值
一线名师指点08高考同步辅导第6讲: 函数的定义域、值域(最大、最小值)
【考点回放】
由给定函数解析式求其定义域这类问题的代表,实际上是求使给定式有意义的x的取值范围它依赖于对各种式的认识与解不等式技能的熟练
1求函数解析式的题型有:
(1)已知函数类型,求函数的解析式:待定系数法;
(2)已知求或已知求:换元法、配凑法;
(3)已知函数图像,求函数解析式;
(4)满足某个等式,这个等式除外还有其他未知量,需构造另个等式:解方程组法;
(5)应用题求函数解析式常用方法有待定系数法等
2求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知的定义域求的定义域或已知的定义域求的定义域:
①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域;
②若已知的定义域,其复合函数的定义域应由解出
3求函数值域的各种方法
函数的值域是由其对应法则和定义域共同决定的其类型依解析式的特点分可分三类:(1)求常见函数值域;(2)求由常见函数复合而成的函数的值域;(3)求由常见函数作某些“运算”而得函数的值域
①直接法:利用常见函数的值域来求
一次函数y=ax+b(a0)的定义域为R,值域为R;
反比例函数的定义域为{x|x0},值域为{y|y0};
二次函数的定义域为R,
当a>0时,值域为{};
当a<0时,值域为{}
②配方法:转化为二次函数,利用二次函数的特征来求值;常转化为型如:的形式;
③分式转化法(或改为“分离常数法”)
④换元法:通过变量代换转化为能求值域的函数,化归思想;
⑤三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;
⑥基本不等式法:转化成型如:,利用平均值不等式公式来求值域;
⑦单调性法:函数为单调函数,可根据函数的单调性求值域
⑧数形结合:根据函数的几何图形,利用数型结合的方法来求值域
⑨逆求法(反求法):通过反解,用来表示,再由的取值范围,通过解不等式,得出的取值范围;常用来解,型如:
【考点解析】
1函数y=的定义域为______,值域为______
答案:[-1,2] ,[0,]
2函数y=的值域是
A[-1,1] B(-1,1] C[-1,1) D(-1,1)
解法一:y==-1
∵1+x2≥1,
∴0<≤2∴-1<y≤1
解法二:由y=,得x2=
∵x2≥0,∴≥0,解得-1<y≤1
解法三:令x=tanθ(-<θ<),
则y==cos2θ
∵-π<2θ<π,
∴-1<cos2θ≤1,即-1<y≤1
答案:B
3. 求下列函数的最大值或最小值:
(1) ;(2);(3)
解:(1),
由得,
∴当时,函数取最小值,
当时函数取最大值
(2)令,则,
∴,
当,即时取等号,∴函数取最大值,无最小值
(3)解法(一)用判别式法:
由得,
①若,则矛盾, ∴,
②由,这时,,
解得:,
且当时,, ∴函数的最大值是,无最小值
解法(二)分离常数法:
由
∵,∴ ,∴函数的最大值是,无最小值
4.(1)函数在上的最大值与最小值的和为,则 2
(2)对于满足的一切实数,不等式恒成立,则的取值范围为
(3)已知函数,,构造函数,定义如下:当时,,当时,,那么( )
有最小值,无最大值 有最小值,无最大值
有最大值,无最小值 无最小值,也无最大值
5.(2006年广东卷)函数的定义域是
A. B. C. D.
解析:由,
答案:故选B.
6.(2006湖北卷)设,则的定义域为
A. B. C. D.
解析:f(x)的定义域是(-2,2),故应有-2<<2且-2<<2解得-4
1,所以不等式可化为x-1>1,即x>2.
【考点演练】
考点1、定义域
1.已知函数的定义域为,函数的定义域为,则( )
解法要点:,,
令且,故.
2.函数,的定义域为________.
3.设函数[ ]D
A.(-1,1) B.(-1,+) C. D.
4.命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充要条件。
命题q:函数y=的定义域是(-∞,-1∪[3,+∞.则
(A)“p或q”为假 (B)“p且q”为真 (C)p真q假 (D)p假q真
5.若函数y=f(2x)的定义域是[1,2],则函数f(的定义域是 (B)
A.[1,2] B.[4,16] C.[0,1] D.[2,4]
考点2、值域
1.求下列函数的值域:
(1); (2); (3);
(4); (5); (6);
(7); (8); (9).
解:(1)
(一)公式法(略)
(二)(配方法)
,
∴的值域为.
2.求函数,的值域.
解:(利用函数的单调性)函数在上单调增,
∴当时,原函数有最小值为;当时,原函数有最大值为.
∴函数,的值域为.
(2)求复合函数的值域:设(),则原函数可化为.
又∵,∴,故,
∴的值域为.
(3)(法一)反函数法:的反函数为,其定义域为,
∴原函数的值域为.
(法二)分离变量法:,
∵,∴,
∴函数的值域为.
(4)换元法(代数换元法):设,则,
∴原函数可化为,∴,
∴原函数值域为.
说明:总结型值域,变形:或
(5)三角换元法:∵,∴设,
则
∵,∴,∴,∴,
∴原函数的值域为.
(6)数形结合法:,∴,∴函数值域为.
(7)判别式法:∵恒成立,∴函数的定义域为.
由得: ①
①当即时,①即,∴
②当即时,∵时方程恒有实根,
∴,∴且,
∴原函数的值域为.
(8),
∵,∴,∴,当且仅当时,即时等号成立.∴,∴原函数的值域为.
(9)(法一)方程法:原函数可化为:,
∴(其中),
∴,∴,∴,∴,
∴原函数的值域为.
(法二)数形结合法:可看作求点与圆上的点的连线的斜率的范围,解略.
3.若关于的方程有实数根,求实数的取值范围.
解:原方程可化为,
令,则,,又∵在区间上是减函数,
∴,即,
故实数的取值范围为:.
l 方法小结:
求函数的值域的方法常用的有:直接法,配方法,判别式法,基本不等式法,逆求法(反函数法),换元法,图像法,利用函数的单调性、奇偶性求函数的值域等.
考点3、求函数的最大值或最小值(列举分析)
1.求下列函数的最大值或最小值:
(1) ;(2);(3).
解:(1),由得,
∴当时,函数取最小值,当时函数取最大值.
(2)令,则,∴,
当,即时取等号,∴函数取最大值,无最小值.
(3)解法(一)用判别式法:
由得,
①若,则矛盾, ∴,
②由,这时,, 解得:,
且当时,, ∴函数的最大值是,无最小值.
解法(二)分离常数法:
由
∵,∴ ,∴函数的最大值是,无最小值.
2.函数的最大值为 16 ;
3.若,则的最大值是 6 ;
4.若则的最小值是;
5.,在和 上是单调递减函数,则的最大值为.
考点4、最值的应用
1.函数在上的最大值与最小值的和为,则 2 .
2.对于满足的一切实数,不等式恒成立,则的取值范围为.
3.已知函数,,构造函数,定义如下:当时,,当时,,那么 ( )
有最小值,无最大值 有最小值,无最大值
有最大值,无最小值 无最小值,也无最大值
l 方法小结:
1.函数的最值问题实质上是函数的值域问题,因此求函数值域的方法,也是求函数的值域的方法,只是答题的方式有所差异;
2.无论用什么方法求最值,都要考查“等号”是否成立,不等式法及判别式法尤其如此.
3.导数也是经常考虑的方法。
【题型讲解】
例1已知函数定义域为(0,2),求下列函数的定义域:
(1) ; (2)
分析:x的函数f(x)是由u=x与f(u)这两个函数复合而成的复合函数,其中x是自变量,u是中间变量由于f(x),f(u)是同一个函数,故(1)为已知0<u<2,即0<x<2求x的取值范围
解:(1)由0<x<2, 得
说明:本例(1)是求函数定义域的第二种类型,即不给出f(x)的解析式,由f(x)的定义域求函数f[g(x)]的定义域关键在于理解复合函数的意义,用好换元法(2)是二种类型的综合
求函数定义域的第三种类型是一些数学问题或实际问题中产生的函数关系,求其定义域,后面还会涉及到
例2已知函数的定义域为,函数的定义域为,则
解:,,
令且,故
∴,故选取
例3求下列函数的值域
① y=3x+2(-1x1) ②
③ ④
解:①∵-1x1,∴-33x3,
∴-13x+25,即-1y5,∴值域是[-1,5]
②∵ ∴
即函数的值域是 { y| y2}
③
∵ ∴
即函数的值域是 { y| yÎR且y¹1}(此法亦称分离常数法)
④当x>0,∴=,
当x<0时,=-
∴值域是[2,+)(此法也称为配方法)
函数的图像为:
∴值域是[2,+)
例4求下列函数的值域:
(1); (2); (3);
(4); (5); (6);
(7); (8); (9)
解:(1)(配方法),
∴的值域为
改题:求函数,的值域
解:(利用函数的单调性)函数在上单调增,
∴当时,原函数有最小值为;当时,原函数有最大值为
∴函数,的值域为
(2)求复合函数的值域:
设(),则原函数可化为
又∵,
∴,故,
∴的值域为
(3)(法一)反函数法:
的反函数为,其定义域为,
∴原函数的值域为
(法二)分离变量法:,
∵,∴,
∴函数的值域为
(4)换元法(代数换元法):设,则,
∴原函数可化为,∴,
∴原函数值域为
说明:总结型值域,变形:或
(5)三角换元法:
∵,∴设,
则
∵,∴,∴,
∴,
∴原函数的值域为
(6)数形结合法:,
∴,
∴函数值域为
(7)判别式法:∵恒成立,∴函数的定义域为
由得: ①
①当即时,①即,∴
②当即时,∵时方程恒有实根,
∴,∴且,
∴原函数的值域为
(8),
∵,∴,∴,
当且仅当时,即时等号成立
∴,∴原函数的值域为
(9)(法一)方程法:原函数可化为:,
∴(其中),
∴,
∴,∴,∴,
∴原函数的值域为
例5求函数的值域
方法一:(判别式法)去分母得 (y-1)+(y+5)x-6y-6=0 ①
当 y¹1时 ∵xÎR ∴△=(y+5)+4(y-1)×6(y+1)0
由此得 (5y+1)0
检验 时 (代入①求根)
∵2 Ï 定义域 { x| x¹2且 x¹3} ∴
再检验 y=1 代入①求得 x=2 ∴y¹1
综上所述,函数的值域为 { y| y¹1且 y¹}
方法二:(分离常数法)把已知函数化为函数
(x¹2)
由此可得 y¹1
∵ x=2时 即
∴函数的值域为 { y| y¹1且 y¹}
例6 (分段函数法及图像法)求函数y=|x+1|+|x-2|的值域
解法1:将函数化为分段函数形式:
,
画出它的图象,由图象可知,函数的值域是{y|y3}
解法2:(几何法或图象法)∵函数y=|x+1|+|x-2|表示数轴上的动点x到两定点-1,2的距离之和,∴易见y的最小值是3,∴函数的值域是[3,+] 如图
例7求函数的值域
解:(换元法)设 则 t0 x=1-
代入得
∵t0 ∴y4
例8设函数,
(1)求函数的定义域;
(2)问是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由
解:(1)由,解得 ①
当时,①不等式解集为;
当时,①不等式解集为,
∴的定义域为
(2)原函数即,
当,即时,函数既无最大值又无最小值;
当,即时,函数有最大值,但无最小值
l 小结:对于二次函数,
⑴若定义域为R时,
①当a>0时,则当时,其最小值;
②当a<0时,则当时,其最大值
⑵若定义域为x [a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b]①若[a,b],则是函数的最小值(a>0)时或最大值(a<0)时,再比较的大小决定函数的最大(小)值②若[a,b],则[a,b]是在的单调区间内,只需比较的大小即可决定函数的最大(小)值
(3)若给定区间不是闭区间,则可能得不到最大(小)值;
(4)当顶点横坐标是字母时,则应根据其对应区间特别是区间两端点的位置关系进行讨论
利用方程思想来处理函数问题,一般称判别式法 判别式法一般用于分式函数,其分子或分母只能为二次式解题中要注意二次项系数是否为0的讨论
求函数值域常用的一些方法(观察法、配方法、判别式法、图象法、换元法等),随着知识的不断学习和经验的不断积累,还有如不等式法、三角代换法等有的题可以用多种方法求解,有的题用某种方法求解比较简捷,同学们要通过不断实践,熟悉和掌握各种解法,并在解题中尽量采用简捷解法
【基础演练】
1函数f(x)与g(x) =3-x的图象关于直线y=x对称,则函数f(x-1)的定义域为
2求下列函数的定义域:
(1)y=; (2)y=
3已知函数f(x)=的定义域为R,则实数a的取值范围是( )
Aa>1/3 B-120,求f(x2)的定义域;
(2)已知函数f(2x)的定义域为[1,2],求f(log2x)的定义域
5已知函数f(x)的定义域为[0,1],g(x)=f(x+a)+f(x-a),求函数g(x)的定义域
6设f(x)=log2+log2(x-1)+log2(p-x)
(1)求函数f(x)的定义域;(2)f(x)是否存在最大值或最小值?如
果存在,请把它写出来;如果不存在,请说明理由
7某宾馆有相同标准的床位100张根据经验,当该宾馆每张床的床价不超过10元时,床位可以全部租出;当床价高于10元时,每提高一元,将有3张床位空闲为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是①为方便结算,床位应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租收入必须高于支出,而且高出得越多越好,若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的支出费用后的收入),
(1)把y表示为x的函数,并求出定义域;
(2)试确定该宾馆床价定为多少时,既符合上述条件,又能使净收入最多?
8求下列函数的值域(1)y=(1-x2)/(1+x2); (2)y=(1-2sinx)/(1+sinx)
9求下列函数的值域:
(1)y=(;(2)y=;(3)y= -
10已知函数f(x)=lg(x2-2mx+m+2)
(1)若f(x)的定义域为R,求实数m的取值范围;
(2)若f(x)的值域为R,求实数m的取值范围
11若函数y=x2-3x-4的定义域为[0,m],值域为[-25/4,-4],则m的取值范围是
12已知f(x)的值域为[3/8,4/9],试求y=f(x)+的值域
13现有直径为d的圆木,要把它锯成横断面为矩形的梁,从材料力学知道,横断面为矩形的木梁强度与梁宽和梁高的平方的乘积成正比,比例系数为k问如何截法才能使梁的强度最大?
14函数y=|x–3|–|x+1|的最大值是
15已知1/2£t£1,则2/t–t的最大值是
16函数y= –x2–2ax(0£x£1)的最大值是a2,那么实数a的取值范围是
17在区间[1/2,2]上函数f(x)=x2+px+q与g(x)=2x+1/x2在同一点取得相同的最小值,那么f(x)在区间[1/2,2]上的最大值是
参考答案:
1 (1,+¥))
2 (1) (0,2)È(2,3], (2) [-5,-3p/2]È(-p/2,p/2)È(3p/2,5]
3 C注意二次项系数为零的特殊情况
4 (1)b>a,b>-a,∴ b>|a|,
a£0时,xÎ[-,],a>0时,xÎ[-,]È [] (2)[4,16]
5当-1/2£a£0时,a<-a£1+a,xÎ[-a,1+a]; 当0£a£1/2时,xÎ[a,1-a];
当a<-1/2或a>1/2时,g(x)不存在
6 (1)11);
(2)f(x)=log2[(x+1)(p-x)]=log2[-(x-)2 +],
当(p-1)/2£1,即13时,f(x)最大值为2log2(p+1)-2,无最小值
7(1)=
(2)当x£10时,y£425;当x>10,则当x=22时,y有最大值约833元
8 (1) (0,1]; (2) [-1/2,+¥)
9 (1)(-1/3£y<1) ;(2)y£1/2;
(3)讨论:x>0时,-1-x-1;当-1£x<时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当£x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
故据此求得最小值为。选C
26.(2006浙江卷)对a,bR,记max|a,b|=函数f(x)=max||x+1|,|x-2||(xR)的最小值是 .
。
解析:由,故
,其图象如右,
则。
27.(2006江西卷)若不等式x2+ax+1³0对于一切xÎ(0,〕成立,则a的最小值是( )
A.0 B. –2 C.- D.-3
解析:设f(x)=x2+ax+1,则对称轴为x=
若³,即a£-1时,则f(x)在〔0,〕上是减函数,应有f()³0Þ
-£x£-1
若£0,即a³0时,则f(x)在〔0,〕上是增函数,应有f(0)=1>0恒成立,故a³0
若0££,即-1£a£0,则应有f()=恒成立,故-1£a£0
综上,有-£a故选C