八年级下数学课件《函数》课件1第二课时_冀教版

八年级下数学课件《函数》课件1第二课时_冀教版

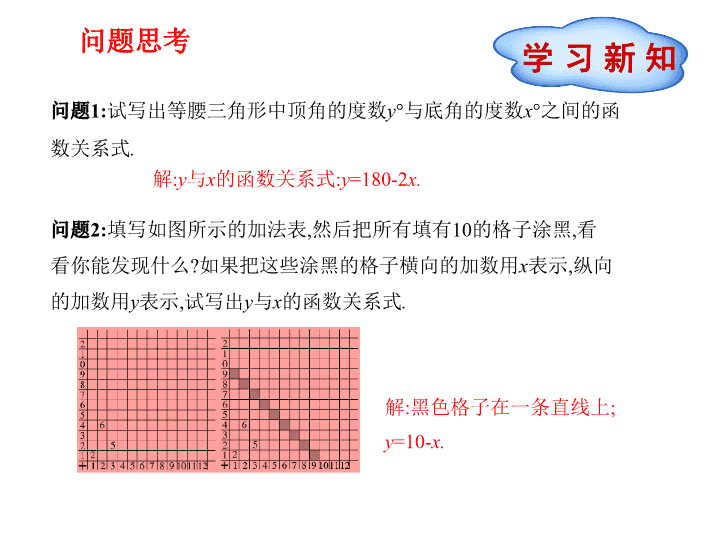
八年级数学·下 新课标[冀教] 第二十章 函 数 学习新知 检测反馈 学 习 新 知问题思考 问题2:填写如图所示的加法表,然后把所有填有10的格子涂黑,看看 你能发现什么?如果把这些涂黑的格子横向的加数用x表示,纵向的 加数用y表示,试写出y与x的函数关系式. 问题1:试写出等腰三角形中顶角的度数y°与底角的度数x°之间的 函数关系式. 解:y与x的函数关系式:y=180-2x. 解:黑色格子在一条直线上; y=10-x. 探究1　探究实际问题中自变量的取值范围 大家谈谈 1.前面讲到的“欣欣报亭的1月~6月的每月纯收入S(元)是月份T的函 数”,其中自变量T可取哪些值?当T=1.5或T=7时,原问题有意义吗? 2.“某市某一天的气温T(℃)是时刻t的函数”,其中自变量t可取哪些 值?如果t取第二天凌晨3时,原问题还有意义吗? 3.“折纸的层数p是折纸次数n的函数”,其中自变量n可取哪些值? 当n=0.5时,原问题有没有意义? 1.T只能取1,2,3,4,5,6这6个整数,当T=1.5或T=7时,原问题(S)无意义. 2.0≤t<24,当t取第二天凌晨3时时,原问题(T)无意义. 3.n≥0,且n是整数,当n=0.5时,原问题(p)无意义. 在用解析式表示函数时,要考虑自变量的取值,必须使解析式有意义. 探究2　函数表达式中自变量的取值范围 求下列函数自变量x的取值范围: (1) 2 1 1(2) (3) 1. y x y x y x      ； ； 明确:在(1)中,由于函数是关于自变量的整式,所 以x为全体实数;在(2)中,由于函数是关于自变量 的分式,必须使分母不为0,所以x≠0;在(3)中,由于 函数是关于自变量的二次根式,所以被开方数为 非负数,即x≥1. 归纳上述结论可知:(相对于已学知识而言)函数自变量的取值范围满 足下列条件: (1)使分母不为零; (2)使二次根式被开方数为非负数; (3)使实际问题有意义. [知识拓展]　函数自变量的取值范围的确定必须考虑两个方面:首 先,自变量的取值必须使含有自变量的代数式有意义;其次,自变量 的取值应使实际问题有意义.这两个方面缺一不可,特别是后者,在 学习过程中容易忽略.因此,在分析具体问题时,一定要细致周到地 从多方面考虑. 探究3　例题讲解 　(教材第67页例题)如图所示,等腰直角三角形ABC的直角边长与 正方形MNPQ的边长均为10 cm,边CA与边MN在同一条直线上,点A与 点M重合.让△ABC沿MN方向运动,当点A与点N重合时停止运动.试写 出运动中两个图形重叠部分的面积y(cm2)与MA的长度x(cm)之间的 函数关系式,并指出自变量的取值范围. 点拨:(1)重叠部分的三角形是什么三角形? (2)怎样表示这个三角形的面积? 1 2 明确:(师生共同归纳)(1)由于△ABC是等腰直 角三角形,得出重叠部分各锐角的度数都是45 度,所以重叠部分的三角形是等腰直角三角 形;(2)函数关系式为y= x2(0≤x≤10). (补充)分别写出下列各问题中的函数关系式及自变量的取值范围. (1)已知等腰三角形的面积为20 cm2,设它的底边长为x(cm),求底边 上的高y(cm)关于x的函数关系式; (2)在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心 圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式. (3)矩形的周长为12 cm,求它的面积S(cm2)与它的一边长x(cm)间的 关系式,并求出当一边长为2 cm时这个矩形的面积. 40y x 解:(1) ,x可取任意正数. (2)S=100π-πr2,r的取值范围是02. 2.写出下列问题中的函数关系式及自变量的取值范围: (1)某市民用电费标准为0.52元/千瓦时,求电费y(元)与用电量x(千 瓦时)的函数关系式. (2)已知一等腰三角形的面积为20 cm2.设它的底边长为x(cm),求 底边上的高y(cm)与x的函数关系式. 40 x 解：(1)y=0.52x,x≥0;(2)y= ,x>0. 求函数自变量取值范围的两个依据: (1)要使函数的解析式有意义. ①函数的解析式是整式时,自变量可取全体实数; ②函数的解析式的分母中含有自变量时,自变量的取 值应使分母≠0; ③函数的解析式是二次根式时,自变量的取值应使被 开方数≥0. (2)反映实际问题的函数关系,自变量的取值应使实际 问题有意义. 检测反馈 2x x 1.(2016·威海中考)函数y= 的自变量x的取值范围是 (　　) A.x≥-2 B.x≥-2且x≠0 C.x≠0 D.x>0且x≠-2 解析:由题意得x+2≥0且x≠0,解得x≥-2且x≠0.故选B. B 1 3x 2.函数y= 的自变量的取值范围是 (　　) A.x≠-3 B.x>-3 C.x≥-3 D.x≤-3 解析:本题考查了使函数解析式有意义的x的取值范围.一般地,从 两个角度考虑:分式的分母不为0;偶次根式被开方数大于或等于0. 当一个式子中同时出现这两点时,应该是取让两个条件都满足的 公共部分,所以x+3>0,解得x>-3.故选B. B 解析:由y=(x-1)0,得x-1≠0,解得x≠1,自变量x的 取值范围是x≠1.故选B. 3.函数y=(x-1)0中,自变量x的取值范围是 (　　) A.x>1 B.x≠1 C.x<1 D.x≥1 4.下列函数中,自变量x的取值范围不正确的是 (　　) A.y=2x2中,x取全体实数 1 1x  2x  1 3x  B.y= 中,x≠1 C.y= 中,x≥2 D.y= 中,x>3 解析:A中的x取全体实数;B中,x+1≠0,得 到x≠-1;C中,x-2≥0,则x≥2;D中,x-3≥0且x- 3≠0,解得x>3.故选B. B B 5.求下列函数中自变量x的取值范围. (1)y=3x-1； 0 1(2) 2 3 ( 1)(3) 2 y x x xy     + ； . 解析:(1)根据对任意的实数都有意义即可求解;(2)根据二次根式的性质 和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的取值 范围;(3)根据0的0次幂无意义即可求解. 解:(1)x是任意实数. 2 0 3 0 x x      ， ，(2)根据题意得 解得x≥2且x≠3. (3)根据题意得x-1≠0,解得x≠1. 6.学校游泳池盛满水2400 m3,出水管每分钟可 放水30 m3,打开出水管,一直到放尽为止,求游 泳池内水量w(m3)与放水时间t(min)的函数关 系式,写出自变量t的取值范围. 解:根据题意,得w=2400-30t(0≤t≤80). 解析:根据“游泳池内水量=2400-放水量”,列 式即可解答. 7.如图所示,正方形ABCD的边长为5,P为BC上一动点(不与B,C 两点重合),若CP=x,△ABP的面积为y,求出y与x之间的函数关系 式,并写出自变量x的取值范围. 解析:由CP=x,得BP=5-x,根据三角形的面积计算方法直接得出函 数解析式,利用P为BC上一动点(不与B,C两点重合)得出自变量的 取值范围即可. 解:∵CP=x,∴BP=5-x, ∴△ABP的面积为y= 1 5 255 5 ) (0 5).2 2 2x x x      （ 8.若一个面积为50 m2的矩形的宽为y(m),长为x(m). (1)直接写出y与x的函数关系式,以及自变量x的取值范围; (2)当长满足5≤x≤10时,求宽y的取值范围. 解析:(1)根据矩形的面积公式可求得y与x的函数关系式;(2)根据 5≤x≤10,可解关于y的不等式组5≤ ≤10得到y的取值范围.50 y 50 y 50 x解:(1)∵xy=50,∴y= (x>0). (2)∵5≤x≤10,∴5≤ ≤10,即5≤y≤10.