- 2021-05-21 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件《用公式法解一元二次方程 3 》参考课件_鲁教版
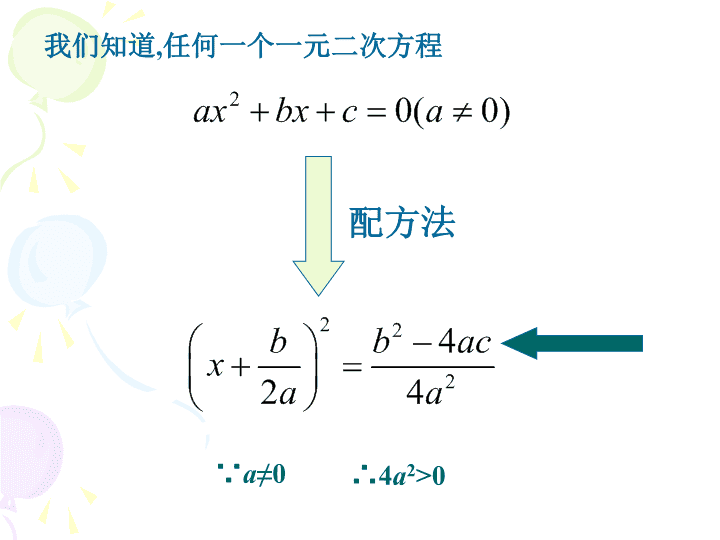
我们知道,任何一个一元二次方程 )0(02 acbxax ∵a≠0 2 2 2 4 2 4 b b acx a a ∴4a2>0 配方法 当 042 acb 时,方程有两个不相等的实数根: 当 042 acb 时, 当 042 acb 时, 方程有两个相等的实数根: 方程没有实数根. , 2 42 1 a acbbx a bxx 221 探 索 a acbbx 2 42 2 2 2 2 ( 0 2 4 4 )b acbx a a a 当 042 acb 时,方程有两个不相等的实数根: 当 042 acb 时, 当 042 acb 时, 方程有两个相等的实数根: 方程没有实数根. , 2 42 1 a acbbx a bxx 221 a acbbx 2 42 2 以上三个结论反过来也是正确的! 我们把 acb 42 叫做一元二次方程 )0(02 acbxax 的根的判别式. 用符号“Δ”来表示. 定 义 acb 42 记住了, 别搞错! 即一元二次方程: 2 0 0ax bx c a 当 时,方程有两个不相等的实数根;0 当 时,方程有两个相等的实数根;0 当 时,方程没有实数根。0 记住了, 别忘了! 当 时,方程有两个不相等的实数根;0≥ 比一比 不解方程,判别下列方程的根的情况: ;01)1( 2 xx ;01)2( 2 xx ;01)3( 2 xx .012)4( 2 xx 不解方程,判别下列方程的根的情况: 例3 解: ∴原方程有两个不相等的实数根 。 原方程可变形为 。 ∴原方程有两个相等的实数根。 (1) (2) 解: 22 4 0x x 2 24 1 4 2 ( 4) 33b ac >0, 24 9 12y y 24 12 9 0,y y 2 24 ( 12) 4 4 9 0b ac , 原方程没有实数根 一般步骤: 3、判别根的情况,得出结论. 1、化为一般式,确定 、 、 的值.a b c 2、计算 的值,确定 的符号. (3)5(t2+1)-6t=0 原方程可变形为 解: 5t2-6t+5=0 2 24 ( 6) 4 5 5 64 0b ac , 不解方程,判别下列方程的根的情况: 2(1)2 6 5 0;y y 2(3)2004 2005 2006 0.x x 练一练 (2)4 ( 5) 25;x x 不解方程,判别下列关于 的方程根的情况:x .022 mmxx 例 .022 mxx变式一 变一变 变式二 .0222 mmxx 变式三 .022 mmxx 你已学会了系数中 含有字母的一元二次方 程的根的情况的判定! 真棒! 结论: acb 42 当a、c异号时, Δ>0. 03)(2 2 xx 游戏 在括号内任意填入一个整数,判 断方程根的情况. acb 42 acb 42 我市现进行危房拆迁改造工作,某建筑工程队, 在工地一边的靠墙处,用120米长的铁栅栏围一 个矩形的临时仓库(如图),铁栅栏只围三边, 问按下列哪个方案可行? 方案一:围成的矩形的面积是1152平方米; 方案二:围成的矩形的面积是1800平方米 方案三:围成的矩形的面积是2000平方米. 已知一元二次方程 有两个不相等的实数根,字母k可取哪些 实数呢? 0)(2 xx k 思考 今天的收获: 我 学 会 了… … 我 掌 握 了… … 我 体 会 到 了… … 一元二次方程 )0(02 acbxax 当Δ>0时,方程有两个不相等的实数根; 当Δ=0时,方程有两个相等的实数根; 当Δ<0时,方程没有实数根. 小结 不解方程,判别下列方程的根的情况: .012 xkx 大显身手 你能在一元二次方程 的括号里,分别填入一个常数,使此方程有 两个不相等的实数根吗? 0)()()( 2 xx 试一试查看更多