- 2021-05-22 发布 |
- 37.5 KB |
- 20页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中化学竞赛辅导大学无机化学第一章-气体液体和溶液的性质
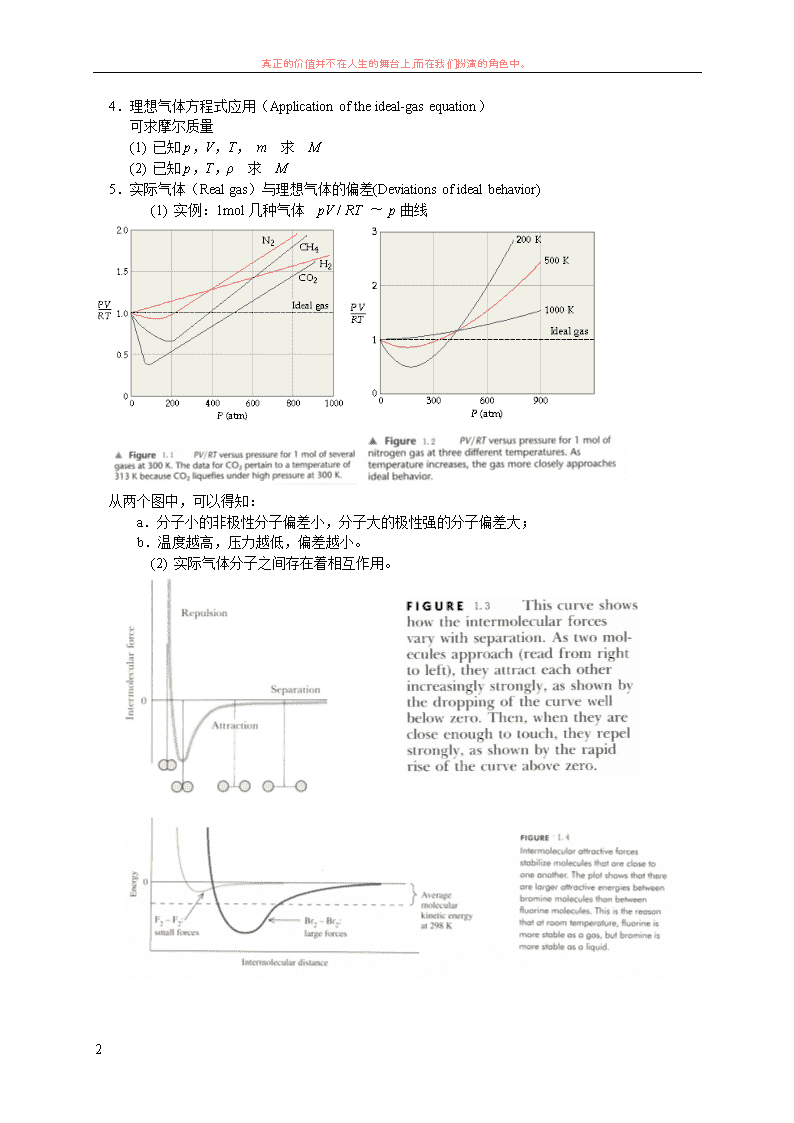
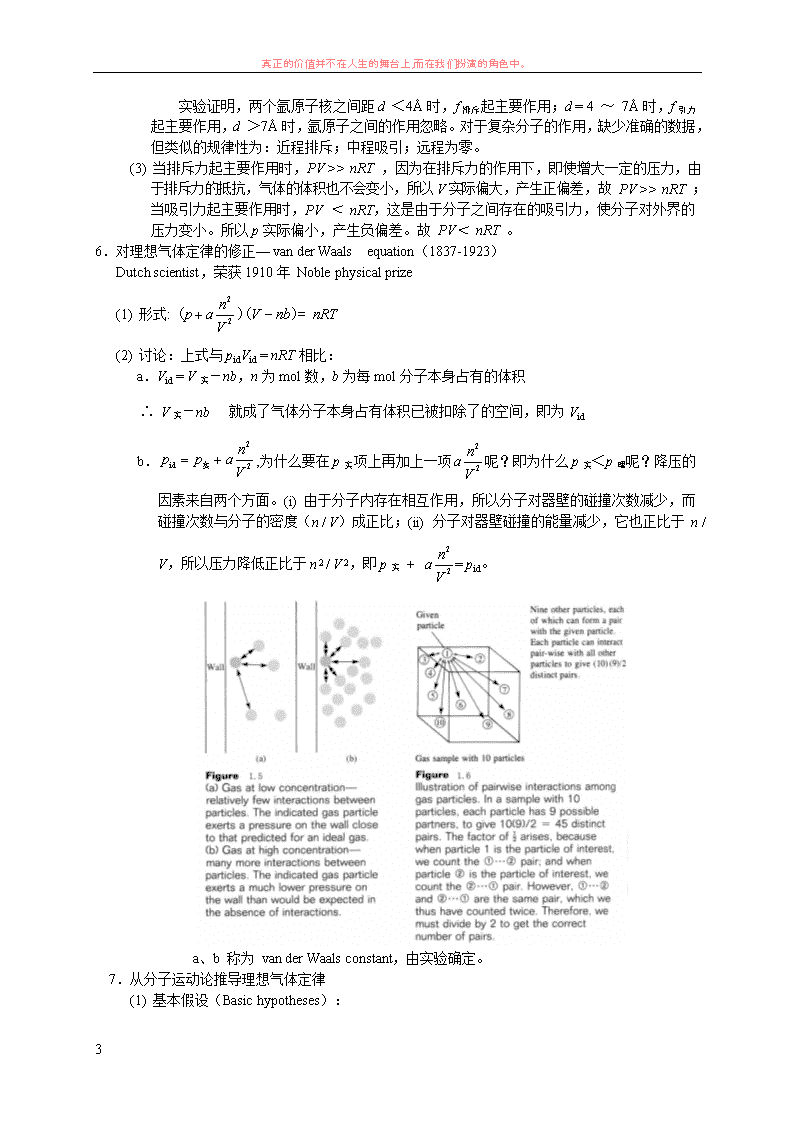
真正的价值并不在人生的舞台上,而在我们扮演的角色中。 1 第一章 气体、液体和溶液的性质 Chapter 1 The Behaviors of Gas、Liquid and Solution §1-1 气体的性质 The Properties of Gases 本节的重点是三个定律: 1.道尔顿分压定律(Dalton’s law of partial pressures) 2.阿码加分体积定律(Amagat’s law of partial volumes) 3.格拉罕姆气体扩散定律(Graham’s law of diffusion) 一、理想气体(Ideal Gases)――讨论气体性质时非常有用的概念 1.什么样的气体称为理想气体? 气体分子间的作用力很微弱,一般可以忽略; 气体分子本身所占的体积远小于气体的体积。 即气体分子之间作用力可以忽略,分子本身的大小可以忽略的气体,称为理想气体。 2.理想气体是一个抽象的概念,它实际上不存在,但此概念反映了实际气体在一定条件下的最一 般的性质。 3.实际气体在什么情况下看作理想气体呢? 只有在温度高和压力无限低时,实际气体才接近于理想气体。因为在此条件下,分子间距 离大大增加,平均来看作用力趋向于零,分子所占的体积也可以忽略。 二、理想气体定律(The Ideal Gas Law) 1.由来 (1) Boyle’s law(1627-1691)British physicist and chemist - The pressure-volume relationship n、T 不变 , V ∝ 1/ p or pV = constant (2) Charles’s law(1746-1823)French scientist 1787 年发现-The temperature-volume relationship n、p 不变 , V ∝ T or V/T = constant (3) Avogadro’s law(1778-1823)Italian physicist Avogadro’s hypothesis :Equal volumes of gases at the same temperature and pressure contain equal numbers of molecular. Avogadro’s law The volume of a gas maintained at constant temperature and pressure is directly proportional to the number of moles of the gas. T、p 不变 , V ∝ n 2.理想气体方程式(The ideal-gas equation) 由上三式得:V ∝ nT / p,即 pV ∝ nT,引入比例常数 R,得:pV = nRT 3.R:Gas constant Units l·atm·mol1·K 1 J·mol1·K1 m3 ·Pa·mol1·K 1 cal·mol1·K1 l·torr·mol1·K1 Numerical Value 0.08206 8.314 8.314 1.987 62.36 在标准状况下: 1.000 0.08206 273.15 22.41(L)1.000 nRTV p 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 2 4.理想气体方程式应用(Application of the ideal-gas equation) 可求摩尔质量 (1) 已知 p,V,T, m 求 M (2) 已知 p,T,ρ 求 M 5.实际气体(Real gas)与理想气体的偏差(Deviations of ideal behavior) (1) 实例:1mol 几种气体 pV / RT ~ p 曲线 从两个图中,可以得知: a.分子小的非极性分子偏差小,分子大的极性强的分子偏差大; b.温度越高,压力越低,偏差越小。 (2) 实际气体分子之间存在着相互作用。 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 3 实验证明,两个氩原子核之间距 d <4Å时,f 排斥起主要作用;d = 4 ~ 7Å时,f 引力起 主要作用,d >7Å时,氩原子之间的作用忽略。对于复杂分子的作用,缺少准确的数据, 但类似的规律性为:近程排斥;中程吸引;远程为零。 (3) 当排斥力起主要作用时,PV >> nRT ,因为在排斥力的作用下,即使增大一定的压力,由 于排斥力的抵抗,气体的体积也不会变小,所以 V 实际偏大,产生正偏差,故 PV >> nRT ; 当吸引力起主要作用时,PV < nRT,这是由于分子之间存在的吸引力,使分子对外界的 压力变小。所以 p 实际偏小,产生负偏差。故 PV< nRT 。 6.对理想气体定律的修正— van der Waals equation(1837-1923) Dutch scientist,荣获 1910 年 Noble physical prize (1) 形式: 2 2 np a V nb nRT V ( )( )= (2) 讨论:上式与 pidVid = nRT 相比: a.Vid = V 实-nb,n 为 mol 数,b 为每 mol 分子本身占有的体积 ∴ V 实-nb 就成了气体分子本身占有体积已被扣除了的空间,即为 Vid b. 2 id 2 np p a V 实 ,为什么要在 p 实项上再加上一项 2 2 na V 呢?即为什么 p 实<p 理呢?降压的因 素来自两个方面。(i) 由于分子内存在相互作用,所以分子对器壁的碰撞次数减少,而碰 撞次数与分子的密度(n / V)成正比;(ii) 分子对器壁碰撞的能量减少,它也正比于 n / V, 所以压力降低正比于 n 2 / V 2,即 p 实 + 2 2 na V = pid。 a、b 称为 van der Waals constant,由实验确定。 7.从分子运动论推导理想气体定律 (1) 基本假设(Basic hypotheses): 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 4 a.物质由分子或原子、离子所组成。同一化学性质的物质,其粒子的大小、形状和作用是 一样的; b.分子作不规则运动; c.气体分子对器壁的碰撞是弹性碰撞。 (2) 推导(Deduction):设边长 L 的一个立方箱子;其中有 N 个气体分子。每个分子的质量为 m, 速度为 u。假设有 N/3 气体分子沿 x 轴方向运动,其动量为 mu。分子撞在左面箱壁 A 后, 以原来的速度向右飞(因为是弹性碰撞),其动量为mu, 因此每撞壁一次,分子的动量就改变了 2mu。一个分子 平均起来看,它向左、向右运动跨越容器,与器壁 A 连 续两次碰撞之间所走的距离为 2L。所以每个分子每秒钟 的动量改变为 2 2 / 2 / mumu L u L N / 3 个分子每秒钟的动量改变为 2 3 N mu f L (单位时间内的动量改变), P(压强)= f / S = f / L2 2 2 33 3 N mu N mu L V p , 即 2 3 NmupV 实际上 ni 个分子,其速度为 ui,作修正: pV = 3 m (n1u12 + n2u22 +… + niui2 + …), i i N n 定义: 2 2 2 2 1 1 2 2 i in u n u n uu N , 2u 称为速率平方的平均值(均值), 代入上式,得 pV= 22 2 1 3 2 3 umNuNm , 动Eum 2 2 1 统计物理学又导出了气体分子的平均动能与温度的关系:单原子分子的平均动能与温 度的关系: kTEK 2 3 ,k-Boltzmann’s constant, 2 3 3 2 NpV kT NkT 与 pV = nRT 作比较:nR = N k,则 k = nR / N,而 N / n = NA 23 1 23 8.314/ 1.381 10 J K6.022 10Ak R N k 的物理意义是分子气体常数 三、道尔顿分压定律(Dalton’s Law of Partial Pressures) 1801 年 1.Deduction:假设有一理想气体的混合物,此混合物本身也是理想气体,在温度 T 下,占有体 积为 V,混合气体各组分为 i(=1,2,3,… i,…) 由理想气体方程式得: L z x y mA Fig. 1.7 An elastic collision of molecule with a well 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 5 1 1 RTp n V , 2 2 RTp n V ,……, i i RTp n V ,…… 总pV RTnV RTnp ii ,即 ipp总 2.表达式: ipp总 3.文字叙述:在温度和体积恒定时,其总压力等于各组分气体单独存在时的压力之和。 4.另一种表达形式: i i i i RTnp nV xRTp nn V 总 ─ mole fraction 在温度和体积恒定时,理想气体混合物中,各组分气体的分压(pi)等于总压(p 总)乘以该组 分的摩尔分数(xi)。 5.实验证明:Ramsay (1852-1916) — British chemist, 荣获 1904 Nobel chemical prize 6.Application of Dalton’s law of partial pressures (1) 求分压: Sample Exercise 1:Suppose that hydrogen is collected over water at 25℃ .How much H2 (expressed in moles) has been collected when the volume of gas is 223 ml under atmospheric pressure of 74.2 cm Hg? Solution: 2 2atm H H Op p p , atmp =74.2 cm Hg The vapor pressure of water at 25℃ is 23.8 mmHg (=2.38 cm Hg) 2 2H atm H O 74.2 2.4 71.8cmHgp p p Solving the ideal gas equation for n, we find 31061.815.29808206.0 223.0)0.76/8.71( RT pVn (mol) (2) 求转化率: Sample Exercise 2:已知某温度、1atm 下,A4B2(g)在密闭容中进行如下分解 A4B2(g) 2A2(g) + B2(g) 达到平衡时,容器的压力为 1.4atm,求 A4B2 的转化率为多少? Solution: Fig. 1.8 Ramsay’s apparatus of verifying the law of partial pressures 如左图:Pd 制小管只允许氢气通过,而不许 氩气通过。在外管通入一定压强的氢气,平衡 后, 2T Ar Hp p p 。不断改变氢气的压强 ( 2 ' Hp 、 2 '' Hp ), 则 2 ' ' T Ar Hp p p , 2 '' '' T Ar Hp p p , Tp 关系式不变,从而验证 了 Dalton 分压定律。 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 6 A4B2(g) 2A2(g) + B2(g) 1 0 0 1α 2α α ∴ 1 1 1 2 1.4 ∴α = 0.2 四、阿玛加分体积定律(Amagat’s Law of Partial Volumes) 1.什么叫分体积:混合气体中某组分 i 单独存在,并且和混合气体的温度,压强相同时,所具有 的体积 Vi ,称为混合气体中第 i 组分的分体积,图示为: T、p 相同时 总体积 V 分体积 V1 分体积 V2 n1 + n2 n1 n2 2.分体积定律:当温度,压力相同时,混合气体的总体积等于各组分分体积之和 3.Deduction: 1 2 1 2 ( ) / / /i i n n n RTnRTV n RT p n RT p n RT pp p 1 2/ / /in RT p n RT p n RT p 1 2 i iV V V V 五、格拉罕姆扩散定律 (Graham’s Law of Effusion and Diffusion) 1.Difference between effusion and diffusion . The mixture of one gas with another is called diffusion. Effusion means gas molecules move from a high-pressure region to a low-pressure region through a pin hole 2.Graham’s law: Thomas Graham discovered that the effusion rate of a gas is inversely proportional to the square root of its molar mass 恒压条件下,某一温度下气体的扩散速率与其密度(或摩尔质量)的平方根成反比 3.表达式: 1 2 2 1 2 1/ / /u u M M 4.验证 (1)实验证实:自白烟圈与管口的距离,可测得两种气体的扩散速率。 (2) 理论推导 由分子运动论的推导可知: 2 23 ( ) 3 u pV mpV Nu N m ∴ 3 / u p N m V ,气体的密度为 N m V ∴当 p = constant , 1u ∴ 1 2 2 1/ /u u 又 ∵ M ∴ 1 2 2 1/ /u u M M 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 7 思考:扩散时间与密度(或摩尔质量)之间的关系如何? 212121 /// MMtt 5.Application of Graham’s law (1) 利用此定律可以测定未知气体的分子量(或原子量),Ramsay 就是利用此法,测定了 Rn 的原子量。 Sample Exercise:An unknown gas composed of homonuclear, diatomic molecules effuses at a rate that is only 0.355 times that of O2 at the same temperature. What is the identity of the unknown gas? Solution: 2 2 2 2 x O O x rate rate M M 2 2 x O rate rate 0.355 ∴ 2x 32.0 0.355M M 2x = 254 g / mol ∴ 原子摩尔质量 = 254× 1 2 = 127 g / mol ∴ We conclude that the unknown gas is I2(g). (2) 可以分离同位素 自然界中 235U 占 0.7%,238U 占 99.3%,235U 可以由热中子诱发裂变,而 238U 不能由热中子 诱发裂变。 从铀矿(pitchblende)(沥青铀矿,UO2)制备 UF6(b. p. = 56℃): 3UO2 + 8HNO3 3UO2(NO3)2 + 2NO + 4H2O 2UO2(NO3)2 300 oC2UO3 + 4NO2 + O2 UO3 + H2 700 oCUO2 + H2O UO2 + 4HF UF4 + 2H2O UF4 + F2 UF6 235 238 6 6 238 235 6 6 UF UF UF UF rate 238.05 6 18.998 352.04 1.0043rate 235.04 6 18.998 349.03 M M 这种微乎其微的差别,要求 gaseous diffusion plant must be very large. The original plant in Oak Ridge Tennessee had 4000 diffusion stage and covered an area of 43 acres(267 亩,1 英亩 = 6.07 亩) §1-2 液体 Liquids 液体所表现出来的特性由其结构特点决定的。它处于完全混乱的气体状态和基本上完全有序的 固体状态之间,所以它既不能象气体运动论那样作基本假设,又不能象固体那样,通过一定的对称 性作一些定量计算,因而液体的定量理论的发展到目前为止还不甚理想。但液体本身也有一些特性, 如:粘度(viscosity)、表面张力(surface tension)、凝固点(freezing point)、沸点(boiling point)、饱和蒸 气压(saturated vapor pressure of liquid),简称为蒸汽压(vapor pressure of liquid)。本节我们主要 讨论液体的饱和蒸气压和凝固点。 一、液体的蒸气压(Vapor Pressure of Liquid) 1.蒸发过程 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 8 (1) 蒸发是液体气化的一种方式,也可以称为相变过程(phase changes)。蒸发过程伴随着能 量的变化(energy changes)。很显然,当液体不能从外界环境吸收能量的情况下,随着液体 的蒸发,液体本身温度下降,蒸发速率也随之减慢。 (2) 液体的蒸发热(heat of vaporization),也称为蒸发焓(enthalpy of vaporization)。 恒压、恒温下,维持液体蒸发所必须的 热量,称为液体的蒸发热。 2.液体的饱和蒸气压(简称蒸气压) (1) 在液体表面,只有超过平均动能的分子,才能 克服邻近分子的吸引,进入气相中-─蒸发。 (2) 在密闭容器中,在不断蒸发的同时,部分蒸气 又会重新回到液体-─凝聚。 (3) 在一定温度下,在密闭容器中,经过一定时间, 蒸发与凝聚达到平衡,这时液 面上的蒸气称为饱和蒸气。 (4) 由饱和蒸气产生的压强称为饱和蒸气压,简 称蒸气压(vapor pressure of liquid)。 (5) 对于同一种液体的蒸气压不决定于液体的体积,也不决定于蒸气体积,只与温度有关,所 以蒸气压仅与液体本质和温度有关。 思考题:蒸气是气体,它是否服从 Boyle’s law? 3.蒸气压与蒸发热的关系(The relationship between vapor pressure and enthalpy of vaporization)-The Clausius—Clapeyron equation((克劳修斯─克拉贝龙方 程式) (1) 以饱和蒸气压的自然对数 ln p 对绝对温度的倒数 (1/T)作图,得到的图象是一条直线,乙醇的 ln p 与 1 / T 的关系如左图,符合下面的直线方程: vapln (1/ ) H p T C R R:gas constant C:直线的截距 ΔvapH:enthalpy of vaporization per mole of substance (2) Clausius-Clapeyron equation 假设在 T1~T2 温度区间内,ΔvapH 不变,蒸气压分别为 p1 和 p2,则 vap 1 1ln (1/ ) H p T C R (1) vap 2 2ln (1/ ) H p T C R (2) (1)-(2)式,得 vap 1 2 2 1 1 1ln( / ) ( ) H p p R T T 或者 vap 1 2 2 1 1 1lg( / ) ( ) 2.303 H p p R T T 此式称为克劳修斯-克拉贝龙方程式。 (3) Application 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 9 a.已知 T1、P1、T2、P2,求 △vapH; b.已知△vapH 和一个温度下的 p,求另一个温度下的 p。 Sample Exercise:The melting point of potassium is 62.3℃. Molten potassium has a vapor pressure of 10.00 torr at 443℃ and a vapor pressure of 400.0 torr at 708℃. Calculate the heat of vaporization of liquid potassium. Solution:By using the Clausius-Clapeyron equation vap1 2 2 1 1 1ln ( ) Hp p R T T ∴ vap10.00 1 1ln ( ) 400.0 8.314 708 273.15 443 273.15 H △vapH = 81.32(kJ · mol1) 二、液体的沸点(Boiling Point of Liquids) 1.液体的沸点是指液体的饱和蒸气压与外界大气压相等时的温度。 2.特征:在此温度下,气化在整个液体中进行,液体表现出沸腾。 3.沸腾与蒸发的区别:蒸发是低于沸点温度下的气化,仅限于在液体表面上进行,所以在沸点以 下的液体气化和达到沸点时液体气化是不同的。 4.The boiling point of a liquid at l atm pressure is called its normal boiling point 三、液体的凝固点(Freezing Point of Liquids) 1.液体的蒸气压与其固体的蒸气压相等时的温度称为液体的凝固点。 2.低于凝固点的液体称为过冷液体(super cooling liquid)。这种现象称为过冷现象(super cooling phenomena)。液体越纯,过冷现象越严重,高纯水可以冷到40℃才开始结冰。因为液体越纯, 结晶中心越难形成。过冷液体是不稳定的状态。结晶一旦开始,体系有趋向平衡的趋势。 3.水的三相点(Triple point):气-液-固三相的平衡点。即纯水在平衡水蒸气压下的凝固点,气、 液、固都是纯净的 H2O。而冰点是指在标准压力下,被空气饱和的水的凝固点,即空气的饱和 水溶液(含有少量 N2、O2、Ar 等)和冰(纯 H2O)的平衡温度。所以水的三相点是指一个纯 净、简单的体系,是一个固定不变的状态;而水的冰点是指一个比较复杂的体系,随外界条件 的不同略有差异。 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 10 Fig. 1.13 Phase diagram of (a) H2O and (b) CO2. The axes are not drawn to scale in either case. In (a), for water, note the triple point A (0.0098℃, 4.58 torr), the normal melting (or freezing) point B (0℃, 1atm), the normal boiling point C (100℃, 1atm), and the critical point D (374.4℃, 217.7atm). In (b), for carbon dioxide, note the triple point X (56.4℃, 5.11atm), the normal sublimation point Y (78.5℃, 1atm), and the critical point Z (31.1℃, 73.0atm). 4.水的临界温度 Tc (Critical temperature) 气液平衡曲线不能无限延长。实验证明其顶点 D 为 374.2℃和 2.21×107 Pa。温度高于 374.2℃, 水只能以气态的形式存在,再加多大外压,气体也不能液化。在 374.2℃以上,既然液态已不再 存在,也没有气—液平衡。所以 D 点是气-液平衡曲线的顶端,就是水的临界状态。 物质的临界点有何特征?什么是超临界流体? 将一个刚性密封容器内部抽成真空,然后充入适量某液体物质(例如,31℃以下充入 CO2)。 在该温度下,该物质会有部分挥发成气态,当达到饱和蒸气压时,气-液两相达到相平衡,液 体表面成为两相的界面。当加热该容器时,容器内温度升高,蒸气压加大,符合 Clausius- Clapeyron 公式。当温度升到某一特定点时(对 CO2,该点温度为 31℃),气-液两相的界面突 然消失,两相变为一相,具有相同的密度,此时的气化热(相变潜热)为零,这一点称为该物 质的临界点(critical point)。 当 T >Tc,p>pc 时的流体称为超临界流体(supercritical fluid)。物质在超临界状态下有一 些特殊的性质: (1) 在临界点附近,其密度与液态的密度数量级类似,而其流动性却更接近气态; (2) 超临界流体的密度随压力的变化改变极大; (3) 物质在超临界状态下可以溶解许多其在液态时不能溶解的物质,而且这种溶解度也随压力的 变化会有极大的改变。 §1-3 溶液 Solutions 一、一些基本概念(Some Basic Concepts) 1.分散系(Dispersion system) (1) 一种或几种物质的质点分散在另一种物质的质点中所形成的体系,称为分散系。分散系中 又分为: 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 11 分散相(dispersion phase) : 被分散的物质称为分散相 分散介质(dispersion medium): 容纳分散相的物质称为分散介质 (2) 分类(Classification): a.均匀分散系(homogeneous dispersion system) b.不均匀分散系(heterogeneous dispersion system) (3) 分散相直径: d < 1nm 溶液 , d = 1~100nm 溶胶 , d > 100nm 悬浊液、乳浊液。 2.溶液(Solutions) (1) 溶液是均匀的分散系。它包括分散相─溶质(solute),分散介质─溶剂(solvent)。 (2) 溶液的种类(kinds of solution) Table 1.1 Examples of Solutions State of Solution State of Solvent State of Solute Example Gas Gas Gas Air Liquid Liquid Gas Oxygen in water Liquid Liquid Liquid Alcohol in water Liquid Liquid Solid Salt in water Solid Solid Gas Hydrogen in palladium Solid Solid Liquid Mercury in silver Solid Solid Solid Silver in gold 3.溶解(Dissolve) (1) 溶解过程是物理化学过程。固体盐的溶解常伴随热效应,两种液体之间的混合常伴 随体积变化,也伴随热效应。 (2) 溶解度(solubility) a.溶解平衡是一个动态平衡(dynamic equilibrium)。 b.饱和溶液的浓度也可以认为是溶解度。溶解度除了用 g/100g H2O 表示, 还可用 mol·dm3 , % 表示。 c.在室温下,s >10g/100g H2O 称为易溶,s 在1~10g/100g H2O 称为可溶,s在 0.1g ~ 1g/100g H2O 称为微溶,s<0.1g/100g H2O 称为难溶。绝对不溶的物质是没有的。 d.影响溶解度的因素: (i) 内因:“相似相溶”:H2O (polar solvent)-离子化合物(Ionic compounds),水-极性 分子(polar molecule)相溶较好 non-polar solvent –non-polar molecule 相溶较好 (ii) 外因:温度(temperature)和压强(pressure) 温度:Solid:温度升高,溶解度有增大,有不变,有减少; Liquid:温度升高,溶解度增大。 ∵ 温度升高液体分子间距增大, ∴ 分子易互溶 Gas:温度升高,溶解度减少。 压强:压强增大时,对固体、液体溶解度变化不大,但对气体的溶解度影响很大。 4.享利定律(Henry’s law)-气体溶解定律 (1) 叙述:在一定温度和一定体积的液体中,所溶解的气体质量与该气体的分压成正比。例如: 0℃、1atm 的 CO2 的溶解度:s0 = 0.335g / 100ml H2O,0℃、2 atm 的 CO2 的溶解度:s0 = 0.670g/100ml H2O 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 12 (2) 解释:当气体的压强增加 n 倍,那么气体进入液体的机会也增加 n 倍,所以气体溶解的质量 也增加 n 倍。故亨利定律与其它气体的分压无关。例如:1atm 的纯氧在水中的溶解度是空 气中氧气的 4.7 倍,因为空气中氧的分压 2Op = 0.21atm。所以若气相中有几种气体,则各种 气体的溶解度皆与其分压成正比。 (3) 数学表达式:kH = p / x (kH:Henry’s constant) p 是被溶解气体的分压(以 mmHg 为单位),x 是溶解的气体在溶液中所占的物质的量 分数。 由于亨利定律有几种不同的叙述方式,浓度,压强都可以用不同的单位,所以在用公式 时,特别要注意亨利定律常数 kH 的单位。 在我们这个表达式中,摩尔分数 (x) 是无量纲的,气体分压 (p) 的单位用 mmHg 柱,所 以 kH 的单位也应是 mmHg 柱。 Sample Exercise:20℃时,氧气溶解在水中的亨利定律常数为 2.95×107mmHg 柱,在通常大气 中,氧分压为 0.21atm,此时有多少摩尔氧气溶在 1000g 水中? Solution: 2O 0.21 760 160(mmHg)p , 7 H 2.95 10 (mmHg)k 由亨利定律 2 2 O O p k x ,得 2 2 6 O O 7 160/ 5.42 10 2.95 10 x p k 2 2 2 O O O 1000 /18 n x n 2O 1000/18 n 2O( 1),n ∴ 2 6 4 O 10005.42 10 3.01 10 18 n (mol) (4) 亨利定律只适用于溶解度小、且不与溶剂相互作用的气体。HCl、NH3 等气体与水有相互作 用,所以它们都不服从亨利定律。 二、溶液的浓度(The Concentrations of Solution) 1.溶液浓度表示法 (1) 质量分数(m/m):(mass fraction, mass percentage),ppm(parts per million),ppb(parts per billion) 饮水中的砷含量不得超过 0.05ppm(= 0.05mg/1L H2O) (2) 体积物质的量浓度(M = n / V)Molarity: 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 13 物质的量浓度(M) = moles of solute/liters of solution (3) 质量物质的量浓度(n / 1000g H2O)Molality: 质量物质的量浓度(m) = moles of solute / kilograms of solvent 当溶液很稀时,ρ = 1,所以 1kg 溶剂近似看作 1L 溶液,则 M ≈ m (4) 摩尔分数(xi)Mole fraction of component: 摩尔分数 xi = n i / n = moles of component/total moles of all components (5) Normality (N)(当量浓度) 当量浓度(N) = n × moles of solute/liters of solution 在酸碱反应中,n 等于参加反应的 H+或 OH-数目,在 Ox-Red 反应中,n 等于 1mol 物质氧 化数的总改变值。离开化学反应讲当量浓度,是毫无意义的。 2.各种浓度之间的换算(Units exchange ) 上面的(1)换算成(2)和(5)必须知溶液的密度,(2)、(5)之间的互换必须知化学反应方程式。 3.各种不同纯度试剂的表示: 优级纯:Guarantee reagent(G. R.) 分析纯:Analytical reagent(A. R.) 化学纯:Chemical reagent(C. R.) 实验试剂:Laboratory reagent(L. R.) 三、稀溶液的依数性(Colligative Properties of Dilute Solution) Colligative 来自拉丁语:colligare,意为团结、一起的意思。依数性指的是仅仅与溶液中微粒的 个数有关的性质,而与溶质的种类无关。 1.溶液的蒸气压降低(Lowering the vapor pressure)──稀溶液依数性的核心 (1) 在一定温度下,向纯溶剂中加入难挥发性的溶质,此溶液的蒸气压仍然是溶剂的蒸气压。 (2) 在一定温度下,溶液的蒸气压小于纯溶剂的蒸气压。 (3) 拉乌尔定律:1880 年法国化学家拉乌尔(Raoult)通过实验发现:溶液的蒸气压下降与溶 质的摩尔分数有关: △ 0 0p p p x p 剂 溶质 剂 ,称为 Raoult’s law. 其中 0p剂 为在某温度下纯溶剂蒸气压,p 为 同一温度下溶液蒸气压。 对于只有一种难挥发溶质的溶液:x 质 + x 剂 = 1 △ 0 0(1 )p p p x p 剂 溶剂 剂 ,故 0p x p 剂 剂 这是一种更常用的形式。文字叙述为:在一定温度下,某难挥发性溶质的溶液的蒸气压等于纯溶剂 的蒸气压乘以溶剂的摩尔分数。 (a) (b) Fig. 1.16 An aqueous solution and pure water in a closed environment. (a) Initial stage, (b) After a period of time, the water is transferred to the solution. Sample Exercise 1:Glycerin, C3H8O3, is a nonvolatile nonelectrolyte with a density of 1.26g/ml at 25℃. Calculate the vapor pressure at 25℃ of a solution made by adding 50.0ml of glycerin to 500.0ml of water. The vapor pressure of pure water at 25℃ is 23.8 torr. 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 14 Solution: Moles of C3H8O3 = 50 1.26 92.1 = 0.684(mol) Moles of H2O = 500 1 18 = 27.8(mol) 976.0681.08.27 8.27 OH2 x )torr(2.238.23976.00 OHOHOH 222 pxp 如果难挥发性的非电解质溶质的溶液很稀时,则 n n剂 质 剂 质 剂质 质 质 n n nn nx , 而 1kg nm 质 质 溶剂 , 等式两边乘以 M 剂 质 剂 质 剂 质 剂质 xn n M nMm /1000 , 把 x 质 m M质 剂 代入Δp 式中 得△ 0p x p M p m K m 质 剂 剂 剂 质 质 ( 0 0, C CK M p T p 剂 剂 剂时, ) 即在一定温度下,某难挥发、非电解质稀溶液的蒸气压下降与其质量物质的量浓度成正比。严 格来讲,这个定律只适合理想溶液(ideal solution)。在受到理想气体的启发下,人们也抽象出一种 理想溶液: a.在理想溶液中,各组分分子是如此相似,以致它们之间的相互作用情况完全一致; b.当各组分分子混合时,不会产生热效应和体积变化。 所以拉乌尔定律的实质是理想溶液中分子的挥发和相应纯液体中的分子完全一样。 (4) 两种挥发性成分组成的溶液(two volatile components),其溶液上方的蒸气压(pT) 如果两种挥发性液体混合成一种溶液,例如 C6H6 (benzene)和 C7H8(toluene)的混合, 没有热效应和体积变化,称为理想溶液,那么这两种液体以任何比例相混合,其溶液均服从 拉乌尔定律。即 p1 = x1p10 , p 2 = x2 p 20 ∴ 溶液上方的蒸气压 0 0 total 1 2 1 1 2 2p p p x p x p Sample Exercise 2:Such a solution, consider a mixture of benzene, C6H6 , and toluene , C7H8 , containing 1.0 mol of benzene and 2.0 mole of toluene (x ben = 0.33 and x tol = 0.67). At 20℃, the vapor pressure of the pure substances are torr750 ben p , .torr220 o ltp Calculate xben in vapor. Solution: torr257533.00 benbenben pxp torr152267.00 toltoltol pxp total ben tol 25 15 40torrp p p ben 25in vapor 0.6315 25x 虽然苯在溶液中仅占 33mol%,但在蒸气中占 63mol %,所以易挥发的成份在蒸气中富积,成为 蒸馏技术(distillation)的重要基础。 (5) 对于挥发性的固体非电解质溶质的溶液,其溶液上方的蒸气压 pT 不饱和溶液时: 0 0 Tp x p x p 质 质 剂 剂 饱和溶液时: 0 0 Tp p x p 质 剂 剂 (即与溶质的摩尔分数无关) 思考题:请学生证明饱和的挥发性的固体非电解质溶质的溶液上方的蒸气压的公式。 2.溶液沸点的升高(Boiling point elevation of solution) 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 15 (1) 由于溶液的蒸气压低于纯溶剂的蒸气压。所以溶液的沸点要高于纯溶剂的沸点,即 Tb > Tb 0 ,△Tb = Tb Tb 0 (2) 由于△p = K·m 质,而与溶液的性质无关,所以,沸点升高的表达式为△Tb=Kb·m, Kb 为 molar boiling point elevation constant。在数值上恰好等于 1m 溶液的沸点上升的度数,其单 位为(℃)K · kg · mol1。 (3) Application: a.已知Tb,求 Kb Sample Exercise :1.00g 尿素[CO(NH2)2]溶解于 75.0g 水中,测得其溶液的沸点为 100.114℃,已知尿 素的分子量为 60.1,求水的 Kb 解: CO(NH2)2 的 1.00 / 60.1 0.222 75/1000 m (m) Tb = 100.114 100 = 0.114℃,Kb = 0.114 / 0.222 = 0.513(℃/m) b.已知Tb,求溶质的摩尔质量 3.溶液的凝固点的降低(Freezing point depression of solution) (1) 由于液体的凝固点是指 0p p 固液 时的温度,而在此温度下, 0p p溶液 液体 , ∴ p 固 > p 溶液。因此只有当温度下降时,由于 p 固下降得更快一点(从上图可以看出), 才能实现 p 固 = p 溶液,这时的温度才是溶液的凝固点 Tf ,由于 Tf <Tf 0 ,所以溶液的凝固点要 低于纯溶剂的凝固点。 (2) 同样由p = K · m,可以把凝固点降低表达式表示为:Tf = Kf · m Kf molar freezing-point depression constant. (3) Application Sample Exercise 1: Automotive antifreeze consists of ethylene glycol , C2H6O2, a nonvolatile nonelectrolyte. Calculate the freezing point of a 25.0 mass percent solution of ethylene glycol in water. Solution: Molality = 25.0 / 62.1 5.37(m) 75/1000 Tf = Kf · m =1.86 × 5.37 = 9.99 ℃ ∴ 5.37m 乙二醇溶液的凝固点 = 0 9.99 = 9.99℃ 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 16 Sample Exercise 2:Lauryl alcohol is obtained from coconut oil and is used to make detergents. A solution of 5.00g of lauryl alcohol in 0.100 kg of benzene freezes at 4.1℃. What is the molar mass of this substance? (Kf = 5.12,Tf 0 = 5.5℃ of benzene) Solution: Tf = 5.5 4.1 = 1.4℃, 由△Tf = Kf · m 得 5.00 /5.12 1.4 0.1 M ,解得 M = 182.9(g · mol1) (4) 凝固点降低法测定分子量比沸点升高法测定分子量更准确。因为 Kf 数值大于 Kb,所以实验 误差相对小一些;其次测凝固点时,可以减少溶剂的挥发。 (5) 对于电解质溶液,m 是指溶液中所有溶质含的离子的质量物质的量浓度。例如 1m NaCl(aq) 中溶质的粒子浓度为 2m。 Sample exercise 3:3.24g Hg(NO3)2 和 10.14g HgCl2 分别溶解在 1000g 水中,溶液的凝固点分别为 0.0558℃和0.0744℃,问哪种盐在水中以离子状态存在?(Kf = 1.86) Solution: Hg(NO3)2 f f 0.588 0.0300 m 1.86 Tm K ( ) 而 (3.24/324)mol 0.01 m 1kg ( ) ∴Hg(NO3)2 在水中以离子状态存在 HgCl2: f f 0.0744 0.0400 m 1.86 Tm K ( ) 而 (10.84/271)mol 0.041 m 1kg ( ) ∴HgCl2 基本上以分子形式存在 Sample exercise 4:List following aqueous solutions in order of their expected freezing points: 0.050m CaCl2、0.15m NaCl、0.10m HCl、0.050m CH3COOH、0.10m C12H22O11 Solution:0.050m CaCl2~0.15m in particles 0.15m NaCl~0.30m 0.10m HCl~0.20m 0.050m CH3COOH~0.05~0.10m 之间 ∴ freezing points’ ordering is NaCl、HCl、CaCl2、C12H12O11、CH3COOH low high 4.渗透压(Osmotic pressure) (1) 半透膜(semipermeable membrane) a.材料:Certain materials, including many membranes in biological systems and synthetic substances such as cellophane, are semipermeable. Cu2[Fe(CN)6] 淀积在素烧粗瓷筒的细 孔内,也有半渗透性。 b.作用:They permit the passage of some molecules but not others. They often permit the passage of small solvent molecules such as water but block the passage of large solute molecules or ions. c.structure: Semipermeable membrane character is a network of tiny pores within the membrane. (2) 渗透(osmosis):溶剂分子通过半透膜从稀溶液向浓溶液方向移动的现象,称为渗透。 There is a net movement of solvent molecules from the less concentrated solution into the more concentrated one. This process is called osmosis. The important point to remember is that the net movement of solvent is always toward the solution with the higher solute concentration. 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 17 (3) 实验(experiment) 图 1 .18 a 中,半透膜左边放入浓溶液,右边放入稀溶液;溶剂从右边移动到左边(就好像 溶液要获得相等的浓度)。由于溶剂的净移动,产生了压力差,如图 1 .18 b,它是由于渗透 引起的,称为渗透压,表现为 U 型管两边的液面差;如果在 U 型管左边加一个压力,可以阻 止溶剂分子的静移动,如图 1 .19。 (4) 1887 年 van’t Hoff(1852-1911)[ 范德霍夫,荷兰物理化学家,曾获 1901 年诺贝尔化学 奖 ] 研究溶液的渗透压,其结论为:溶质分散在一定体积的溶剂中的渗透压和溶质扩散 在等体积中的气体压力一样,即:πV = nRT or π = cRT (The osmotic pressure is found to obey a law similar in form to the ideal gas law) 注意:a.此公式只适用于非电解质稀溶液;b.在极稀溶液中,一升溶液近似看作 1kg 溶 剂,所以π ≈ mRT;c.只有在半透膜存在下,才能表现出渗透压;d.虽然稀溶液 的π = cRT 与气体的 pV = nRT 完全符合,但π与 p 产生的原因是不同。 (5) Application a.求分子量。渗透压常用于极高分子量的物质的测定。 Sample exercise 1:在 250C、1 升苯中含 5.0 克聚苯乙烯的溶液,其π = 7.6mmHg,试求聚苯乙烯的分 子量? Solution:π = 7.6 / 760 = 0.01(atm) 5.0n M , T= 298K 由π = cRT 得 5.0 / M RT V 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 18 ∴ 5.0 5.0 0.08206 298 0.01 1 RTM V = 1.22×104(g / mol) 故聚苯乙烯的分子量为 1.22×104 b.配制等渗溶液(isotonic solution):渗透压相等的溶液,例如红血球的渗透压与 0.9%的 NaCl(aq)的渗透压相同。若把血液放入小于 0.9%NaCl 溶液中,水就渗入红血球 中,红血球溶涨,可使红血球破裂,称为溶血作用(hemolysis);若把血液放入大于 0.9% 的 NaCl 溶液中,红血球中的水分就渗出,红血球缩小(shrive),所以大量的静脉注射必 须配制与血液相等的渗透压才能应用,否则会引起严重的疾病。 Sample exercise 2:The average osmotic pressure of blood is 7.7 atm at 25℃. What concentration of glucose, C6H12O6, will be isotonic with blood? Solation:由π = cRT 得 7.7 0.310.08206 298c RT (mol / L) c.可使海水淡化 5.稀溶液依数性的总结 (1) 当难挥发性的非电解质溶解在溶剂中形成极稀溶液,它的蒸气压降低、沸点升高、凝固点 降低以及渗透压,与在一定量的溶剂或一定体积的溶液中所溶解的溶质的摩尔数成正比, 而与溶质的本质无关。我们把这种溶液在性质上变化的规律性称为稀溶液的依数性 (colligative properties) (2) 蒸气压降低、沸点升高和凝固点降低都是由 x 剂或 m 质来决定的,因此它们之间有 联系,蒸气压下降是核心。正是由于蒸气压的下降,引起了沸点升高和凝固点降低。 四、胶体溶液(Colloidal Solution) 1.胶体的定义:分散相粒子的直径在 1~100nm 范围内的均匀分散系。 2.胶态体系有 8 种(gas-gas 除外),我们研究固体分散在液体中的胶态体系-溶胶(sol-gel)。 3.溶胶制备(preparation): (1) 凝聚法 a.物理凝聚法: (i) 更换介质法:硫的洒精溶液倒入水中形成硫溶胶; (ii) 蒸气凝聚法:在特制的反应器中,蒸发钠金属与有机化合物(苯),在蒸气相中形 成钠溶胶(aerosol)。 b.化学凝聚法: (i) 还原法制 Au 溶胶:2HAuCl4 + 3H2O2 2Au + 8HCl + 3O2 (ii) 氧化法制硫溶胶:2H2S + SO2 3S + 2H2O (iii) 分解法制镍溶胶:Ni(CO)4 Ni(苯中)+ 4CO (iv) 水解法制 Fe2O3 水溶胶:2FeCl3 + (3 + x )H2O Fe2O3 · xH2O + 6HCl (2) 分散法 :机械、电、超声波等分散,胶体磨分散。 4.溶胶的特性: 除了高分子溶液的溶胶外,溶胶的分散相与分散介质之间存在着明显的物理界面 (1) 丁铎尔效应(Tyndall’s effect): 溶胶粒子质点大,散射能力大,只要λ~d 质点,就可发生散射。 (2) 电泳现象(Electrophoresis): 在电流的作用下,胶体粒子的定向移动。这说明溶胶粒子带同性电荷,如果电场中固 相不动而液相流动,称为电渗析(Electro-osmosis) 正电荷胶体:Fe、Cd、Al、Cr、Pb、Ce、Th、Ti 等氢氧化物溶胶 负电荷胶体:Au、Ag、Pt、S 等溶胶,As2S3、Sb2S3、H2SiO3、锡酸等。 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 19 (3) 溶胶不稳定,放置一定时间,会沉淀出来,若再加入分散介质,不能再形成溶胶,这是不 可逆的。 (4) 高分子溶液是一个均匀体系,分散介质和分散相之间无界面,但分子直径 100nm-1nm 之间,一般不带电荷,比溶胶稳定。高分子溶液的溶解是可逆的,它具有稀溶液的依数性, 也具有丁铎尔效应,但无电泳现象。 (5) 胶体分成两类:亲液胶体和疏液(憎液)胶体。前者指大分子溶液,是热力学稳定体系; 后者则属于热力学不稳定的非均相体系,主要靠动力学稳定性和界面电荷维持体系的相 对稳定,胶体化学主要研究后一类体系。 5.胶粒带同种电荷的原因 (1) Liepatoff’s rule(李伯托夫规则):胶粒总是选择性的吸附与它本身结构相似的离子。 (2) 实例: a.SiO2 溶胶:表面 SiO2 + H2O H2SiO3 SiO32 + 2H+,[SiO2]m 胶粒吸附 SiO32,使硅胶带负电荷 b.Fe(OH)3 胶体:FeCl3 水解,生成 Fe(OH)3,一部分 Fe(OH)3 与盐酸反应生成 FeOCl,FeOCl 电离,生成 FeO+和 Cl-,胶粒[Fe(OH)3]m 吸附 FeO+而带正电荷 c.KI(aq)和 AgNO3(aq)反应,制备 AgI 溶胶:当 AgNO3 过量时,AgI 溶胶吸附 Ag+离子,带 正电荷;若 KI 过量时;AgI 溶胶吸附 I-离子,带负电荷。 (3) 溶胶的胶团结构书写: a.氢氧化铁溶胶: { [Fe(OH)3]m nFeO+ ,(n x)Cl }x+ xCl. . 吸附层 扩散层 胶粒 胶团 胶核 表面离子 束缚反离子 自由反离子 b.硅胶溶液 胶粒 胶团 胶核 表面离子 束缚反离子 自由反离子 { [SiO2]m nSiO3 2 ,2(n x)H+ }2x 2xH+. . 6.溶胶的聚沉和保护方法 (1) 溶胶的聚沉(Coagulation) a.加入电解质:(i) 反离子电荷数越高,聚沉越快(Al3+>Mg2+>Na+),v ∝ (离子 电荷数)6;(ii) 反离子的水合半径越小,越易聚沉;(iii) 反离子越易吸附,越易聚沉;b.加 入相反电荷的溶胶;c.升高温度。 (2) 溶胶的保护:加入适当的高分子溶胶,但量太少会发生敏化作用,反而起不到保护作用。 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 20查看更多