【数学】2020年高考真题——北京卷(word版无答案)
2020年普通高等学校招生全国统一考试(北京卷)
数学
本试卷共5页,150分,考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将本试卷和答案卡一并交回。
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合A=-1,0,1,2,B=x0
0的解集是( )
A. -1,1
B. -∞,-1∪1,+∞
C. 0,1
D. -∞,0∪1,+∞
7.设抛物线的顶点为O,焦点为F,准线为l,P是抛物线上异于O的一点,过P作PQ⊥l于Q,则线段FQ的垂直平分线( )
A.经过点O
B.经过点P
C.平行于直线OP
D.垂直于直线OP
8.在等差数列an中,a1=-9,a5=-1,记Tn=a1a2…ann=1,2,…,则数列Tn( )
A.有最大项,有最小项
B.有最大项,无最小项
C.无最大项,有最小项
D.无最大项,无最小项
9.已知α,β∈R,则“存在k∈Z使得α=kπ+-1kβ”是“sinα=sinβ”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
10.2020年3月14日是全球首个国际圆周率日(π Day).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值,按照阿尔·卡西的方法,π的近似值的表达式是( )
A.3n(sin30°n+tan30°n)
B.6n(sin30°n+tan30°n)
C.3n(sin60°n+tan60°n)
D.6n(sin60°n+tan60°n)
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
11.函数f(x)=1x+1+lnx的定义域是_________.
12.已知双曲线C:x26-y23=1,则C的右焦点的坐标为_________: C的焦点到其渐近线的距离是_________.
13.已知正方形ABCD的边长为2,点P满足AP=12(AB+AC),则PD=_________;PB⋅PD=_________.
14.若函数f(x)=sin(x+φ)+cosx的最大值为2,则常数φ的一个取值为_________.
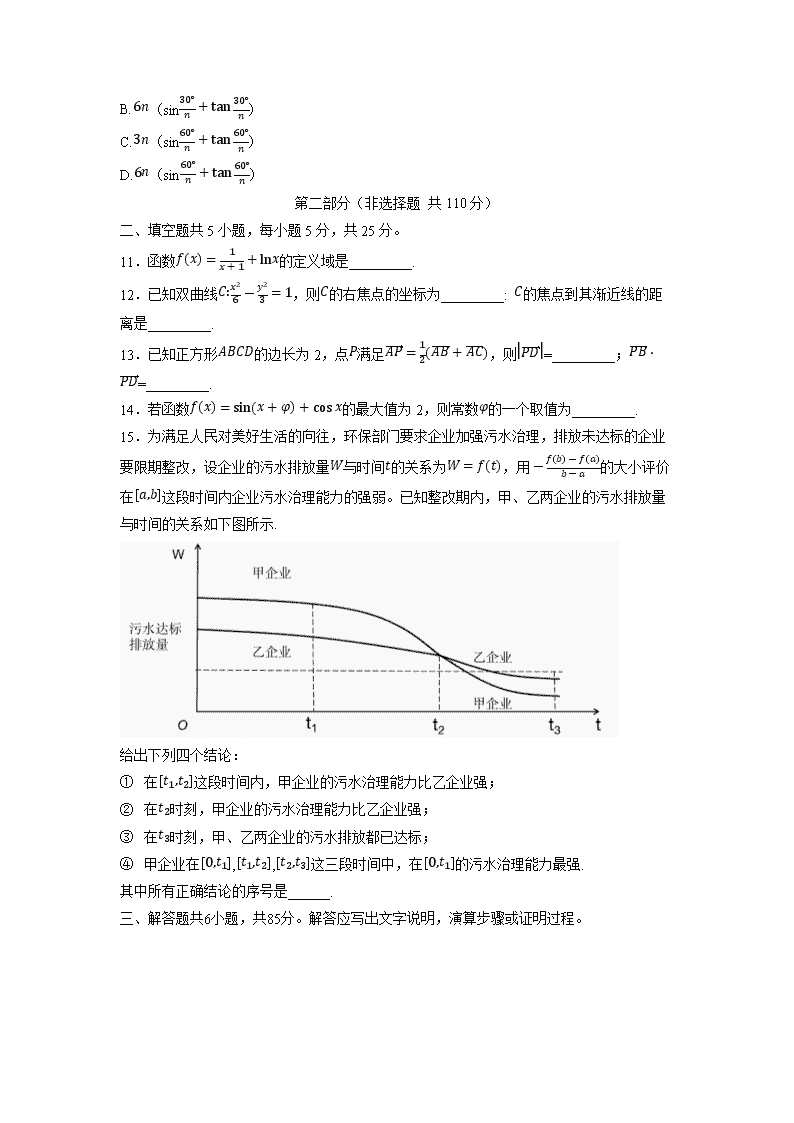
15.为满足人民对美好生活的向往,环保部门要求企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为W=f(t),用-f(b)-f(a)b-a的大小评价在[a,b]这段时间内企业污水治理能力的强弱。已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
① 在[t1,t2]这段时间内,甲企业的污水治理能力比乙企业强;
② 在t2时刻,甲企业的污水治理能力比乙企业强;
③ 在t3时刻,甲、乙两企业的污水排放都已达标;
④ 甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中,在[0,t1]的污水治理能力最强.
其中所有正确结论的序号是______.
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
综合题分割
16.(本小题13分)
如图,在正方体ABCD-A1B1C1D1中,E为BB1的中点,
(Ⅰ)求证: BC1∥平面AD1E;
(Ⅱ)求直线AA1与平面AD1E所成角的正弦值。
综合题分割
17.(本小题13分)
在△ABC中,a+b=11, 再从条件①、条件②这两个条件中选择一个作为已知, 求:
(I) a的值;
(II) sinC 和△ABC的面积.
条件①: c=7, cosA=-17;
条件②: cosA=18,cosB=916。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
综合题分割
18.(本小题14分)
某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二。为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生
女生
支持
不支持
支持
不支持
方案一
200人
400人
300人
100人
方案二
350人
250人
150人
250人
假设所有学生对活动方案是否支持相互独立。
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案二的概率估计值记为p0。假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为p1,试比较p0与p1的大小。(结论不要求证明)
综合题分割
19.(本小题15分)
已知函数f(x)=12-x2。
(Ⅰ)求曲线y=f(x)的斜率等于-2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的最小值.
综合题分割
20.(本小题15分)
已知椭圆C:x2a2+y2b2=1过点A(-2,-1),且a=2b。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(-4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x=-4于点P,Q.求|PB||BQ|的值.
综合题分割
21.(本小题15分)
已知{an}是无穷数列,给出两个性质:
①对于{an}中任意两项ai,aj(i>j),在{an}中都存在一项am,使得ai2aj=am;
②对于{an}中任意一项an(n≥3),在{an}中都存在两项ak,al(k>l),使得an=ak2al.
(Ⅰ)若an=n(n=1,2,...),判断数列{an}是否满足性质①,说明理由;
(Ⅱ)若an=2n-1(n=1,2,...),判断数列{an}是否同时满足性质①和性质②,说明理由;
(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.