- 2021-05-22 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全等三角形 教案
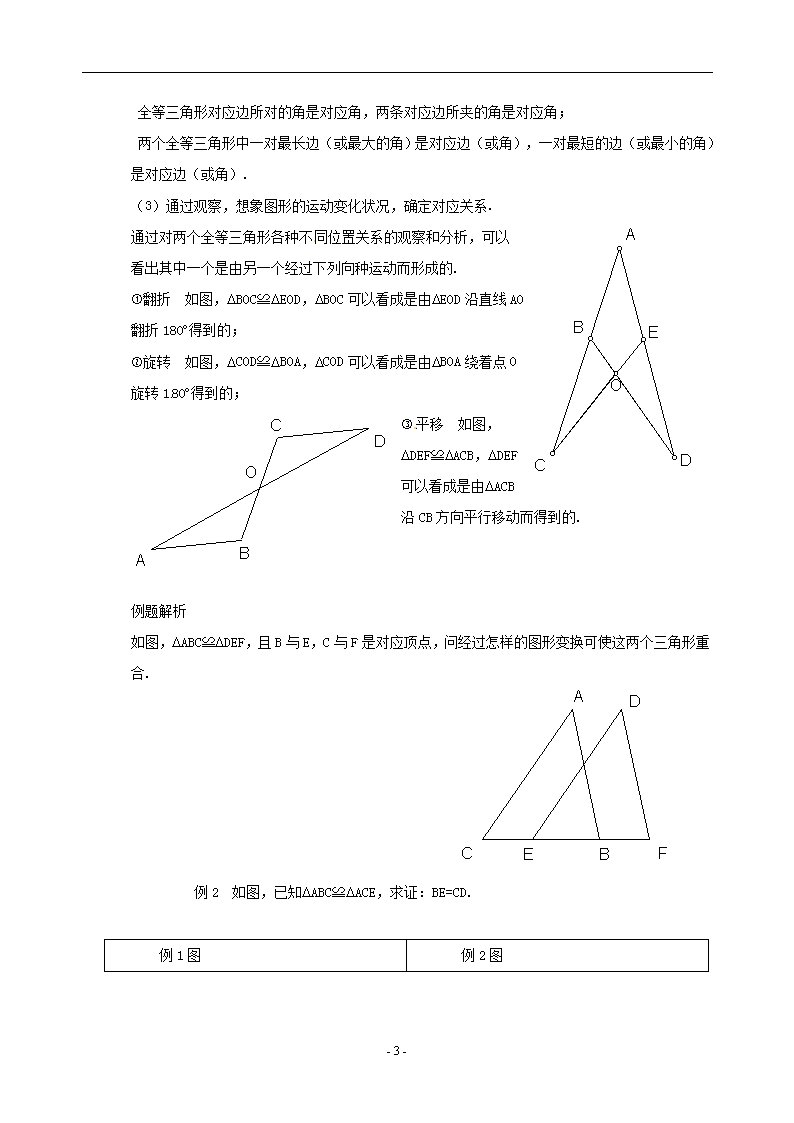
全等三角形 学习要求: 1.知识方面: (1)知道什么是全等形、全等三角形及全等三角形的对应元素; (2)知道全等三角形的性质,能用符号正确地表示两个三角形全等; (3)能熟练找出两个全等三角形的对应角、对应边. 2.能力方面: (1)通过全等三角形角有关概念的学习,提高学生数学概念的辨析能力; (2)通过找出全等三角形的对应元素,培养学生的识图能力. 3.情感方面: (1)通过感受全等三角形的对应美激发学生热爱科学勇于探索的精神; (2)通过自主学习的发展体验获取数学知识的感受,培养学生勇于创新,多方位审视问题的创造技巧. 学习重点:全等三角形的性质. 学习难点:找全等三角形的对应边、对应角 教学过程: 一、全等形及全等三角形概念的引入 我们身边经常看到“一模一样”的图形,比如两张由同一底片冲印出来的完全相同的照片,用两张纸重叠在一起剪出的两张窗花等,你还能举一些这样的“一模一样”的例子吗? 1.问题(1):几何中,我们把上面所列举的“一模一样”的图形叫做“全等形”,那么我们怎么给“全等形”下一个几何定义呢? (1)形状相同的两个图形? (2)大小相等的两个图形? (3)能够完全重合的两个图形? 讨论结果:能够完全重合的两个图形叫全等形. 问题(2):你们知道什么叫全等三角形? 能够完全重合的两个三角形叫全等三角形 两个全等三角形中,相互重合的顶点叫做对应顶点,相互重合的边叫对应边,互相重合的角叫对应角。 2.全等三角形的表示方法:若△ABC和△A′B′C′是全等的三角形,记作 “△ABC≌△A′B′ - 4 - C′ 其中,“≌”读作“全等于”.记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上. 二 全等三角形性质 1.问题:全等三角形有什么性质呢? 如图:△ABC和△DEF重合,它们是全等的,其中顶点A,D重合,它们是对应顶点;AB边与DE边重合, 它们是对应边;∠A与∠D重合,它们是对应角. 你能找出其他的对应顶点、对应边和对应角吗? 全等三角形性质:全等三角形的对应边相等,对应角相等. 问题探究:1.画一条直线,把正方形分成全等的两部分.这样的直线有多少条? 2.一个等边三角形,你能把它分成两个全等的三角形吗? 你能把它分成三个、四个全等的三 角形吗? 三 练习题:1.如图△ABC≌△DCE, ∠A与∠D为对应角,DC⊥CE于C, AB⊥BC于C.找出对应角和对应边 . 〔分析〕 因为DC⊥CE于C,AB⊥BC于C , 所以∠B= ∠DCE,于是∠B和 ∠DCE是对应角.那么,它们所对的边就是对应边. 2. 如图△ABC≌△DBC, BC平分∠ABD.写出相等的角和相等的边 . 〔分析〕 因为BC平分∠ABD,所以∠ABC= ∠DBC, 于是∠ABC和 ∠DBC是对应角.那么,它们所对的边就是对应边.又因为BC是这两个三角形的公共边,所以它们所对的角就是对应角. 四 . 寻找对应元素的方法 (1)根据对应顶点找 如果两个三角形全等,那么,以对应顶点为顶点的角是对应角;以对应顶点为端点的边是对应边. 通常情况下,两个三角形全等时,对应顶点的字母都写在对应的位置上,因此,由全等三角形的记法便可写出对应的元素. 如DABC≌DDEF,则其对应元素如下: 对应顶点:A¬®D,B¬®E,C¬®F; 对应边 :AB¬®DE,BC¬®EF,AC¬®DF; 对应角 :ÐABC¬®ÐDEF,ÐBCA¬®ÐEFD, ÐCAB¬®ÐFDE; (2)根据已知的对应元素寻找 全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边; - 4 - 全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角; 两个全等三角形中一对最长边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角). (3)通过观察,想象图形的运动变化状况,确定对应关系. 通过对两个全等三角形各种不同位置关系的观察和分析,可以看出其中一个是由另一个经过下列向种运动而形成的. 翻折 如图,DBOC≌DEOD,DBOC可以看成是由DEOD沿直线AO翻折180°得到的; 旋转 如图,DCOD≌DBOA,DCOD可以看成是由DBOA绕着点O旋转180°得到的; 平移 如图,DDEF≌DACB,DDEF可以看成是由DACB沿CB方向平行移动而得到的. 例题解析 如图,DABC≌DDEF,且B与E,C与F是对应顶点,问经过怎样的图形变换可使这两个三角形重合. 例2 如图,已知DABC≌DACE,求证:BE=CD. 例1图 例2图 - 4 - 本课小结:找对应边、对应角通常有下面几种方法: 全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边; 全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角; 有公共边的,公共边一定是对应边; 有公共角的,公共角一定是对应角; 有对顶角的,对顶角是对应角; 两个全等三角形中一对最长边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角). 五 作业: A组 1.如图, △AOD≌△COB, ∠A= ∠C,找出这两个三角形的对应角和对应边 . 2.如图,△ABD≌△ACE, ∠B= ∠C,找出这两个三角形的对应角和对应边 . A组1 A组2 B组 1.已知:如图,△ABC≌△FED,且BC=ED. 求证:AB∥EF,AD=FC. 2.已知:如图,B是AC的中点,BD=CE,AD=BE,BD∥CE,AD∥BE求证:△ABD≌△BCE. B组 1 B组2 - 4 -查看更多