2020年江苏省常州市中考数学一模试卷
2020年江苏省常州市中考数学一模试卷
一、选择题(每题2分,共16分)
1. 下列各数中,互为倒数的是( )
A.−3与3 B.−3与13 C.−3与−13 D.−3与|−3|
2. 五箱苹果的质量(单位:kg)分别为:19,22,21,20,19,则这五箱苹果质量的众数和中位数分别为( )
A.19和21 B.19和20 C.19和19 D.19和22
3. 下列运算正确的是( )
A.x6÷x2=x4 B.(x3y)2=x5y2
C.−2(x−1)=−2x+1 D.(x−1)2=x2−1
4. 图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.① B.② C.③ D.④
5. 关于x的一元二次方程x2+ax−1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
6. 如图,直线y=kx+b与x轴交于点(−4, 0),则y>0时,x的取值范围是( )
A.x<−4 B.x>0 C.x>−4 D.x<0
7. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A.24 B.14 C.13 D.23
8. 如图,四边形ABCD、CEFG是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
①BE⊥GD;②OH=12BG;③∠AHD=45∘;④GD=2AM,
其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题2分,共20分)
−2的绝对值等于________.
函数y=2x−4中,自变量x的取值范围是________.
每天供给地球光和热的太阳与我们距离非常遥远,它距地球15000000千米,将15000000千米用科学记数法表示为________千米.
在平面直角坐标系中,点P(−1, 2)向右平移3个单位长度得到的点的坐标是________.
计算aa−1+11−a的结果是________.
分解因式:a3−4a=________.
第25页 共28页 ◎ 第26页 共28页
如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32∘,则∠D=________度.
已知一个扇形的半径为6cm,圆心角为150∘,则这个扇形的面积为 15π cm2.
如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45∘,将△DAE绕点D逆时针旋转90∘,得到△DCM.若AE=1,则FM的长为________.
如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=kx(k≠0, x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为________.
三、解答题(共10小题,满分84分)
计算:
(1)4sin60∘−12−(12)−1
(2)(a−2b)(a+2b)−(a−2b)2
解不等式组:x+1<3x+12−1<2x3 ,并把解集在数轴上表示出来.
如图,△EBF为等腰直角三角形,点B为直角顶点,四边形ABCD是正方形.
(1)求证:△ABE≅△CBF;
(2)CF与AE有什么特殊的位置关系?请证明你的结论.
某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.
根据以上信息,解答下列问题:
(1)这次调查一共抽取了________名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是________;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有________名.
数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.
(1)李老师随机抽取一张卡片,抽到卡片B的概率等于________;
第25页 共28页 ◎ 第26页 共28页
(2)求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
某社区计划对1200m2的区域进行绿化,经投标由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且甲、乙两队在分别独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y关于x的函数关系式.
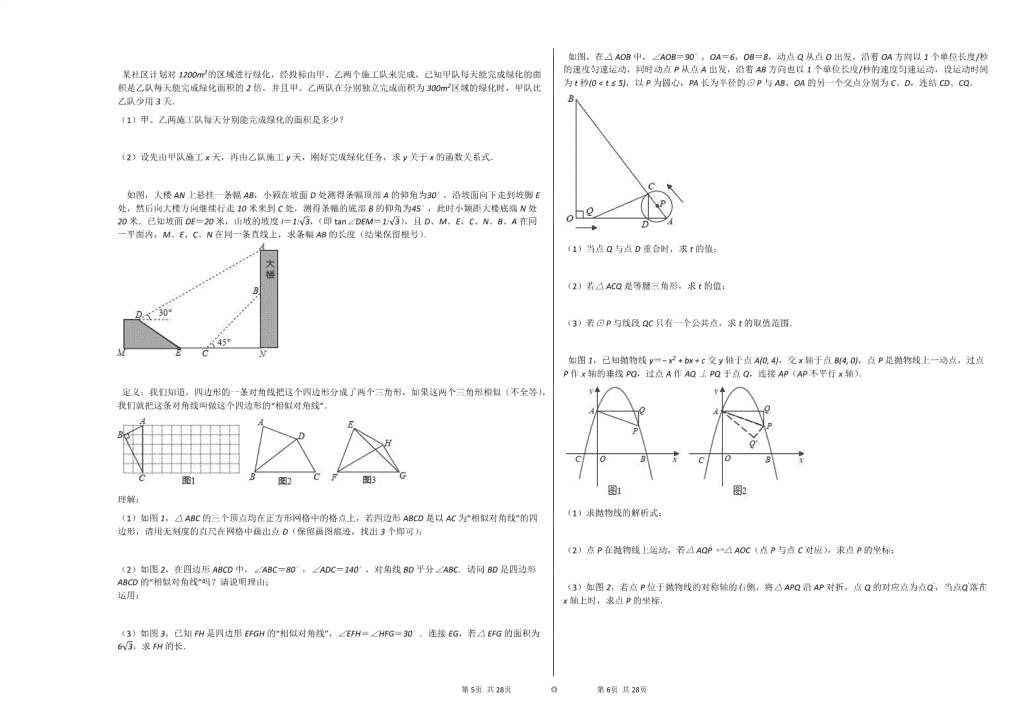
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30∘,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45∘,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:3,(即tan∠DEM=1:3),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).
定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80∘,∠ADC=140∘,对角线BD平分∠ABC.请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30∘.连接EG,若△EFG的面积为63,求FH的长.
如图,在△AOB中,∠AOB=90∘,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0
0,
∴ 方程有两个不相等的实数根.
故选D.
6.
【答案】
C
【考点】
一次函数的性质
一次函数图象上点的坐标特点
【解析】
观察函数图象可知:y随x的增大而增大,结合直线y=kx+b与x轴交于点(−4, 0),即可得出当y>0时x的取值范围.
【解答】
观察函数图象,可知:y随x的增大而增大.
∵ 直线y=kx+b与x轴交于点(−4, 0),
∴ 当y>0时,x>−4.
7.
【答案】
A
【考点】
相似三角形的性质与判定
解直角三角形
第25页 共28页 ◎ 第26页 共28页
矩形的性质
【解析】
证明△BEF∽△DAF,得出EF=12AF,EF=13AE,由矩形的对称性得:AE=DE,得出EF=13DE,设EF=x,则DE=3x,由勾股定理求出DF=DE2−EF2=22x,再由三角函数定义即可得出答案.
【解答】
解:∵ 四边形ABCD是矩形,
∴ AD=BC,AD // BC,
∵ 点E是边BC的中点,
∴ BE=12BC=12AD,
∴ △BEF∼△DAF,
∴ EFAF=BEAD=12,
∴ EF=12AF,
∴ EF=13AE.
∵ 点E是边BC的中点,
∴ 由矩形的对称性得:AE=DE,
∴ EF=13DE.
设EF=x,则DE=3x,
∴ DF=DE2−EF2=22x,
∴ tan∠BDE=EFDF=x22x=24.
故选A.
8.
【答案】
D
【考点】
四边形综合题
【解析】
①由已知条件可证得△BEC≅△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90∘,所以∠BDC+∠DBH+∠CDG=90∘,即BE⊥GD,故①正确;
②由①可以证明△BHD≅△BHG,就可以得到DH=GH,得出OH是△BGD的中位线,从而得出结论.
③若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45∘,所以②的结论也是正确的.
④此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45∘,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;
【解答】
①正确,证明如下:
∵ BC=DC,CE=CG,∠BCE=∠DCG=90∘,
∴ △BEC≅△DGC,
∴ ∠EBC=∠CDG,
∵ ∠BDC+∠DBH+∠EBC=90∘,
∴ ∠BDC+∠DBH+∠CDG=90∘,即BE⊥GD,故①正确;
②∵ BE平分∠DBC,
∴ ∠DBH=∠GBH.
∵ BE⊥GD,
∴ ∠BHD=∠BHG=90∘.
在△BHD和△BHG中
∠DBH=∠GBHBH=BH∠BHD=∠BHG ,
∴ △BHD≅△BHG(ASA),
∴ DH=GH.
∵ O是BD中点,
∴ DO=BO.
∴ OH是△BDG的中位线,
∴ OH=12BG,故②正确;
③由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45∘,故③正确;
④由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵ ∠ABD=∠DBG=45∘,
∴ △ABM∽△DBG,得AM:DG=AB:BD=1:2,即DG=2AM;
故④正确;
∴ 正确的个数有4个.
二、填空题(每题2分,共20分)
【答案】
2
【考点】
绝对值
【解析】
根据负数的绝对值等于它的相反数即可求解.
【解答】
|−2|=2.
【答案】
x≥2
【考点】
二次根式有意义的条件
函数自变量的取值范围
【解析】
因为当函数表达式是二次根式时,被开方数为非负数,所以2x−4≥0,可求x的范围.
【解答】
2x−4≥0
解得x≥2.
【答案】
1.5×107
第25页 共28页 ◎ 第26页 共28页
【考点】
科学记数法--表示较大的数
【解析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】
15000000=1.5×107.
【答案】
(2, 2)
【考点】
坐标与图形变化-平移
【解析】
将点P的横坐标加3,纵坐标不变即可求解.
【解答】
点P(−1, 2)向右平移3个单位长度得到的点的坐标是(−1+3, 2),即(2, 2).
【答案】
1
【考点】
分式的加减运算
【解析】
原式变形后,利用同分母分式的减法法则计算即可得到结果.
【解答】
原式=aa−1−1a−1
=a−1a−1
=1.
【答案】
a(a+2)(a−2)
【考点】
提公因式法与公式法的综合运用
【解析】
原式提取a,再利用平方差公式分解即可.
【解答】
原式=a(a2−4)
=a(a+2)(a−2).
【答案】
26
【考点】
圆周角定理
切线的性质
【解析】
连接OC,根据圆周角定理得到∠COD=2∠A,根据切线的性质计算即可.
【解答】
连接OC,
由圆周角定理得,∠COD=2∠A=64∘,
∵ CD为⊙O的切线,
∴ OC⊥CD,
∴ ∠D=90∘−∠COD=26∘,
【答案】
根据扇形的面积公式,得
S扇=150π×62360=15π(cm2).
【考点】
扇形面积的计算
【解析】
根据扇形的面积=nπR2360,进行计算.
【解答】
根据扇形的面积公式,得
S扇=150π×62360=15π(cm2).
【答案】
52
【考点】
正方形的性质
全等三角形的性质与判定
旋转的性质
【解析】
由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90∘,由∠EDF=45∘,得到∠MDF为45∘,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;则可得到AE=CM=1,正方形的边长为3,用AB−AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM−FM=BM−EF=4−x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为FM的长.
【解答】
∵ △DAE逆时针旋转90∘得到△DCM,
∴ ∠FCM=∠FCD+∠DCM=180∘,
∴ F、C、M三点共线,
∴ DE=DM,∠EDM=90∘,
∴ ∠EDF+∠FDM=90∘,
∵ ∠EDF=45∘,
∴ ∠FDM=∠EDF=45∘,
在△DEF和△DMF中,
DE=DM∠EDF=∠FDMDF=DF ,
∴ △DEF≅△DMF(SAS),
∴ EF=MF,
设EF=MF=x,
∵ AE=CM=1,且BC=3,
∴ BM=BC+CM=3+1=4,
∴ BF=BM−MF=BM−EF=4−x,
∵ EB=AB−AE=3−1=2,
在Rt△EBF
第25页 共28页 ◎ 第26页 共28页
中,由勾股定理得EB2+BF2=EF2,
即22+(4−x)2=x2,
解得:x=52,
∴ FM=52.
【答案】
154
【考点】
菱形的性质
反比例函数的性质
反比例函数图象上点的坐标特征
【解析】
过点D作DF⊥BC于点F,由菱形的性质可得BC=CD,AD // BC,可证四边形DEBF是矩形,可得DF=BE,DE=BF,在Rt△DFC中,由勾股定理可求DE=1,DF=3,由反比例函数的性质可求k的值.
【解答】
如图,过点D作DF⊥BC于点F,
∵ 四边形ABCD是菱形,
∴ BC=CD,AD // BC
∵ ∠DEB=90∘,AD // BC
∴ ∠EBC=90∘,且∠DEB=90∘,DF⊥BC
∴ 四边形DEBF是矩形
∴ DF=BE,DE=BF,
∵ 点C的横坐标为5,BE=3DE,
∴ BC=CD=5,DF=3DE,CF=5−DE
∵ CD2=DF2+CF2,
∴ 25=9DE2+(5−DE)2,
∴ DE=1
∴ DF=BE=3,
设点C(5, m),点D(1, m+3)
∵ 反比例函数y=kx图象过点C,D
∴ 5m=1×(m+3)
∴ m=34
∴ 点C(5, 34)
∴ k=5×34=154
三、解答题(共10小题,满分84分)
【答案】
原式=4×32−23−2
=23−23−2
=−2;
原式=a2−4b2−(a2−4ab+4b2)
=a2−4b2−a2+4ab−4b2
=4ab−8b2.
【考点】
负整数指数幂
特殊角的三角函数值
平方差公式
完全平方公式
实数的运算
【解析】
(1)根据特殊角的三角函数值,二次根式的性质以及负整数指数幂的定义计算即可;
(2)根据平方差公式以及完全平方公式计算即可.
【解答】
原式=4×32−23−2
=23−23−2
=−2;
原式=a2−4b2−(a2−4ab+4b2)
=a2−4b2−a2+4ab−4b2
=4ab−8b2.
【答案】
x+1<3x+12−1<2x3 ,
由①得:x<2,
由②得:x>−3,
不等式组的解集为:−3−3,
不等式组的解集为:−30,
∴ k=10,
∴ EF=10米,DF=103米,
∴ DH=DF+EC+CN=103+30(米),
在Rt△ADH中,tan∠ADH=AHDH=33,
∴ AH=33×DH=10+103,
∴ AN=AH+EF=20+103(米),
∵ 在Rt△BCN中,∠BCN=45∘,
∴ CN=BN=20,
∴ AB=AN−BN=103(米),
【答案】
如图1所示.AB=5,BC=25,∠ABC=90∘,AC=5,
∵ 四边形ABCD是以AC为“相似对角线”的四边形,
①当∠ACD=90∘时,△ACD∽△ABC或△ACD∽△CBA,
∴ ACAB=CDBC或ACBC=CDAB,
∴ 55=CD25或525=CD5,
∴ CD=2.5或CD=10,
同理:当∠CAD=90∘时,AD=2.5或AD=10,
如图中,D1,D2,D3,D4即为所求.
如图2,BD是四边形ABCD的“相似对角线”,
理由如下:
∵ ∠ABC=80∘,BD平分∠ABC,
∴ ∠ABD=∠DBC=40∘,
∴ ∠A+∠ADB=140∘,
∵ ∠ADC=140∘,
∴ ∠BDC+∠ADB=140∘
∴ ∠A=∠BDC,
∴ △ABD∽△DBC,
∴ BD是四边形ABCD的“相似对角线”;
如图3,
∵ FH是四边形EFGH的“相似对角线”,
∴ △EFH与△HFG相似.
又∠EFH=∠HFG,
∴ △FEH∽△FHG,
∴ FEFH=FHFG,
∴ FH2=FE⋅FG,
过点E作EQ⊥FG垂足为Q,
可得EQ=FE×sin60=32FE,
∵ 12FG×EQ=63,
∴ 12FG×32FE=63,
∴ FG⋅FE=24,
∴ FH2=FG⋅FE=24,
∴ FH=26.
【考点】
作图-相似变换
角平分线的性质
勾股定理
【解析】
(1)先求出AB,BC,AC,再分情况求出CD或AD,即可画出图形;
(2)
第25页 共28页 ◎ 第26页 共28页
先判断出∠A+∠ADB=140∘=∠ADC,即可得出结论;
(3)先判断出△FEH∽△FHG,得出FH2=FE⋅FG,再判断出EQ=32FE,继而求出FG⋅FE=24,即可得出结论.
【解答】
如图1所示.AB=5,BC=25,∠ABC=90∘,AC=5,
∵ 四边形ABCD是以AC为“相似对角线”的四边形,
①当∠ACD=90∘时,△ACD∽△ABC或△ACD∽△CBA,
∴ ACAB=CDBC或ACBC=CDAB,
∴ 55=CD25或525=CD5,
∴ CD=2.5或CD=10,
同理:当∠CAD=90∘时,AD=2.5或AD=10,
如图中,D1,D2,D3,D4即为所求.
如图2,BD是四边形ABCD的“相似对角线”,
理由如下:
∵ ∠ABC=80∘,BD平分∠ABC,
∴ ∠ABD=∠DBC=40∘,
∴ ∠A+∠ADB=140∘,
∵ ∠ADC=140∘,
∴ ∠BDC+∠ADB=140∘
∴ ∠A=∠BDC,
∴ △ABD∽△DBC,
∴ BD是四边形ABCD的“相似对角线”;
如图3,
∵ FH是四边形EFGH的“相似对角线”,
∴ △EFH与△HFG相似.
又∠EFH=∠HFG,
∴ △FEH∽△FHG,
∴ FEFH=FHFG,
∴ FH2=FE⋅FG,
过点E作EQ⊥FG垂足为Q,
可得EQ=FE×sin60=32FE,
∵ 12FG×EQ=63,
∴ 12FG×32FE=63,
∴ FG⋅FE=24,
∴ FH2=FG⋅FE=24,
∴ FH=26.
【答案】
∵ OA=6,OB=8,∠AOB=90∘
∴ AB=OA2+OB2=62+82=10,
由题意知:OQ=AP=t,
∴ AC=2t,
∵ AC是⊙P的直径,
∴ ∠CDA=90∘,
∴ CD // OB,
∴ △ACD∽△ABO,
∴ ACAB=ADAO,
∴ AD=65t,
当Q与D重合时,AD+OQ=OA,
∴ 65t+t=6,
∴ t=3011.
(Ⅰ)若AC=AQ,则2t=6−t 得:t=2.
若AC=QC,则AD=QD,即:6t5×2=6−t,
解得:t=3017.
(Ⅲ)若AQ=QC,则AQ2=QC2,
由△ACD∽△ABO,
∴ ACAB=CDBO,可得:CD=8t5,
即:(6−t)2=(8t5)2+(6−t−6t5)2,
解得:t1=94,t2=0(舍去),
(注:第(Ⅲ)情况,连接QP,利用△AQP∽△ABO可得:APAO=AQAB即:t6=6−t10则更简单).
综上所述,满足条件的t的值为2或
第25页 共28页 ◎ 第26页 共28页
3017或94.(1)当QC与⊙P相切时,
此时∠QCA=90∘,
∵ OQ=AP=t,
∴ AQ=6−t,AC=2t,
∵ ∠A=∠A,∠QCA=∠O,
∴ △AQC∽△ABO,
∴ AQAB=ACAO,
∴ 6−t10=2t6,
∴ t=1813,
∴ 当032),
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4−(−m2+3m+4)=m2−3m,
∵ △APQ沿AP对折,点Q的对应点为点Q′,
∴ ∠AQ′P=∠AQP=90∘,AQ′=AQ=m,PQ′=PQ=m2−3m,
∵ ∠AQ′O=∠Q′PH,
∴ Rt△AOQ′∽Rt△Q′HP,
∴ OA:Q′H=AQ′:Q′P,解得Q′H=4m−12,
∴ OQ′=m−(4m−12)=12−3m,
在Rt△AOQ′中,42+(12−3m)2=m2,
整理得m2−9m+20=0,解得m1=4,m2=5,此时P点坐标为(4, 0)或(5, −6);
综上所述,点P的坐标为(4, 0)或(5, −6).
【考点】
二次函数综合题
【解析】
(1)利用待定系数法求抛物线解析式,然后利用抛物线解析式得到一元二次方程,通过解一元二次方程得到C点坐标;
(2)利用△AQP∽△AOC得到AQ=4PQ,设P(m, −m2+3m+4),所以m=4|4−(−m2+3m+4|,然后解方程4(m2−3m)=m和方程4(m2−3m)=−m得P点坐标;
(3)设P(m, −m2+3m+4)(m>32),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2−3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′H=4m−12,则OQ′=12−3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12−3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2−3m|=m,然后解方程m2−3m=m和方程m2−3m=−m得此时P点坐标.
【解答】
把A(0, 4),B(4, 0)分别代入y=−x2+bx+c得 c=4−16+4b+c=0 ,
解得b=3c=4 ,
∴ 抛物线解析式为y=−x2+3x+4.
当y=0时,−x2+3x+4=0,解得x1=−1,x2=4,
∴ C(−1, 0),
∴ OC=1,
∵ A(0, 4),
∴ OA=4,
∵ △AQP∽△AOC,
∴ AQAO=PQCO,
∴ AQPQ=AOCO=4,即AQ=4PQ,
设P(m, −m2+3m+4),
∴ m=4|4−(−m2+3m+4|,即4|m2−3m|=m,
解方程4(m2−3m)=m得m1=0(舍去),m2=134,此时P点坐标为(134, 5116);
解方程4(m2−3m)=−m得m1=0(舍去),m2=114,此时P点坐标为(114, 7516);
综上所述,点P的坐标为(134, 5116)或(114, 7516).
第25页 共28页 ◎ 第26页 共28页
设P(m, −m2+3m+4)(m>32),
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4−(−m2+3m+4)=m2−3m,
∵ △APQ沿AP对折,点Q的对应点为点Q′,
∴ ∠AQ′P=∠AQP=90∘,AQ′=AQ=m,PQ′=PQ=m2−3m,
∵ ∠AQ′O=∠Q′PH,
∴ Rt△AOQ′∽Rt△Q′HP,
∴ OA:Q′H=AQ′:Q′P,解得Q′H=4m−12,
∴ OQ′=m−(4m−12)=12−3m,
在Rt△AOQ′中,42+(12−3m)2=m2,
整理得m2−9m+20=0,解得m1=4,m2=5,此时P点坐标为(4, 0)或(5, −6);
综上所述,点P的坐标为(4, 0)或(5, −6).
第25页 共28页 ◎ 第26页 共28页