- 2021-05-21 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
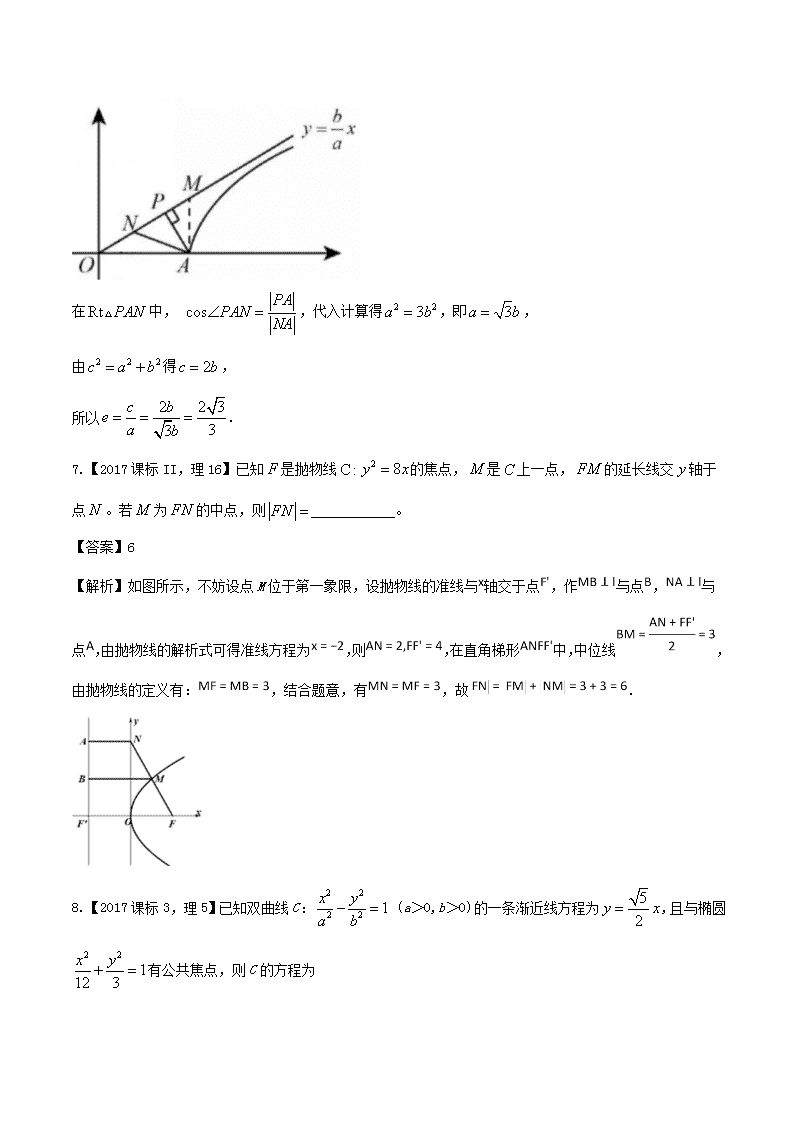
专题15椭圆双曲线抛物线易错起源高考数学理备考黄金易错点Word版含解析
1.【2017课标1,理10】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为 A.16 B.14 C.12 D.10 【答案】A 2.【2017课标II,理9】若双曲线(,)的一条渐近线被圆所截得的弦长为2,则的离心率为( ) A.2 B. C. D. 【答案】A 【解析】由几何关系可得,双曲线的渐近线方程为,圆心到渐近线距离为,则点到直线的距离为, 即,整理可得,双曲线的离心率.故选A. 3.【2017浙江,2】椭圆的离心率是 A. B. C. D. 【答案】B 【解析】,选B. 4.【2017天津,理5】已知双曲线的左焦点为,离心率为.若经过和两点的直线平行于双曲线的一条渐近线,则双曲线的方程为 (A) (B)(C)(D) 【答案】B 【解析】由题意得 ,选B. 5.【2017北京,理9】若双曲线的离心率为,则实数m=_________. 【答案】2 【解析】 ,所以 ,解得 . 6.【2017课标1,理】已知双曲线C:(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________. 【答案】 【解析】如图所示,作,因为圆A与双曲线C的一条渐近线交于M、N两点,则为双曲线的渐近线上的点,且, , 而,所以, 点到直线的距离, 在中, ,代入计算得,即, 由得, 所以. 7.【2017课标II,理16】已知是抛物线的焦点,是上一点,的延长线交轴于点。若为的中点,则 。 【答案】6 【解析】如图所示,不妨设点M位于第一象限,设抛物线的准线与轴交于点,作与点,与点,由抛物线的解析式可得准线方程为,则,在直角梯形中,中位线,由抛物线的定义有:,结合题意,有,故. 8.【2017课标3,理5】已知双曲线C: (a>0,b>0)的一条渐近线方程为,且与椭圆有公共焦点,则C的方程为 A. B. C. D. 【答案】B 【解析】双曲线C: (a>0,b>0)的渐近线方程为 , 椭圆中: ,椭圆,即双曲线的焦点为 , 据此可得双曲线中的方程组: ,解得: , 则双曲线 的方程为 . 故选B. 9.【2017山东,理14】在平面直角坐标系中,双曲线的右支与焦点为的抛物线交于两点,若,则该双曲线的渐近线方程为 . 【答案】 【解析】 , 因为 ,所以渐近线方程为. 10.【2017课标1,理20】已知椭圆C:(a>b>0),四点P1(1,1),P2(0,1),P3(–1,),P4(1,)中恰有三点在椭圆C上. (1)求C的方程; (2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l 过定点. 【答案】(1).(2)见解析。 (2)设直线P2A与直线P2B的斜率分别为k1,k2, 如果l与x轴垂直,设l:x=t,由题设知,且,可得A,B的坐标分别为(t, ),(t, ). 则,得,不符合题设. 从而可设l: ().将代入得 由题设可知. 设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=. 而 . 由题设,故. 即. 解得. 当且仅当时, ,欲使l: ,即, 所以l过定点(2, ) 易错起源1、圆锥曲线的定义与标准方程 例1、(1)△ABC的两个顶点为A(-4,0),B(4,0),△ABC周长为18,则C点轨迹方程为( ) A.+=1(y≠0) B.+=1(y≠0) C.+=1(y≠0) D.+=1(y≠0) (2)在平面直角坐标系中,已知△ABC的顶点A(-4,0)和C(4,0),顶点B在椭圆+=1上,则=________. 答案 (1)D (2) 解析 (1)∵△ABC的两顶点A(-4,0),B(4,0),周长为18,∴|AB|=8,|BC|+|AC|=10.∵10>8,∴点C到两个定点的距离之和等于定值,满足椭圆的定义,∴点C的轨迹是以A,B为焦点的椭圆,∴2a=10,2c=8,∴b=3.∴椭圆的标准方程是+=1(y≠0).故选D. (2)由椭圆方程知其焦点坐标为(-4,0)和(4,0),恰分别为△ABC的顶点A和C的坐标,由椭圆定义知|BA|+|BC|=2a=10,在△ABC中,由正弦定理可知,===. 【变式探究】(1)已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为30°,则该双曲线的标准方程为( ) A.-=1 B.-=1 C.-=1 D.-=1 (2)抛物线y2=4x上的两点A,B到焦点的距离之和为8,则线段AB的中点到y轴的距离为________. 答案 (1)B (2)3 (2)设A(x1,y1),B(x2,y2),由抛物线的定义及题意知,x1+1+x2+1=8,∴x1+x2=6. ∴线段AB的中点到y轴的距离为3. 【名师点睛】 (1)准确把握圆锥曲线的定义和标准方程及其简单几何性质,注意焦点在不同坐标轴上时,椭圆、双曲线、抛物线方程的不同表示形式.(2)求圆锥曲线方程的基本方法就是待定系数法,可结合草图确定. 【锦囊妙计,战胜自我】 1.圆锥曲线的定义 (1)椭圆:|PF1|+|PF2|=2a(2a>|F1F2|); (2)双曲线:||PF1|-|PF2||=2a(2a<|F1F2|); (3)抛物线:|PF|=|PM|,点F不在直线l上,PM⊥l于M. 2.求解圆锥曲线标准方程“先定型,后计算” 所谓“定型”,就是曲线焦点所在的坐标轴的位置;所谓“计算”,就是指利用待定系数法求出方程中的a2,b2,p的值. 易错起源2、圆锥曲线的几何性质 例2 (1)椭圆Γ:+=1(a>b>0)的左,右焦点分别为F1,F2,焦距为2c.若直线y=(x+c)与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________. (2)已知双曲线-=1的左、右焦点分别为F1、F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( ) A.y=±3x B.y=±2x C.y=±(+1)x D.y=±(-1)x 答案 (1)-1 (2)C 解析 (1)直线y=(x+c)过点F1(-c,0),且倾斜角为60°,所以∠MF1F2=60°,从而∠MF2F1=30°,所以MF1⊥MF2.在Rt△MF1F2中,|MF1|=c,|MF2|=c, 所以该椭圆的离心率e===-1. (2)由题意作出示意图, 易得直线BC的斜率为,cos∠CF1F2=, 又由双曲线的定义及|BC|=|CF2|可得 |CF1|-|CF2|=|BF1|=2a, |BF2|-|BF1|=2a⇒|BF2|=4a, 故cos∠CF1F2==⇒b2-2ab-2a2=0⇒()2-2()-2=0⇒=1+, 故双曲线的渐近线方程为y=±(+1)x. 【变式探究】(1)设椭圆C:+=1(a>b>0)的左,右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则椭圆C的离心率为( ) A. B. C. D. (2)设双曲线-=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D,若D到直线BC的距离小于a+,则该双曲线的渐近线斜率的取值范围是( ) A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞) C.(-,0)∪(0,) D.(-∞,-)∪ (,+∞) 答案 (1)D (2)A 解析 (1)因为PF2⊥F1F2,∠PF1F2=30°, 所以|PF2|=2c·tan30°=c,|PF1|=c. 又|PF1|+|PF2|=c=2a,所以==, 即椭圆C的离心率为. (2)由题作出图象如图所示. 由-=1可知A(a,0),F(c,0). 易得B,C. ∵kAB==, ∴kCD=. ∵kAC==, ∴kBD=-. ∴lBD:y-=-(x-c), 即y=-x++, lCD:y+=(x-c), 即y=x--. ∴xD=c+. ∴点D到BC的距离为. ∴查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档