中考数学压轴题1

中考数学压轴题1

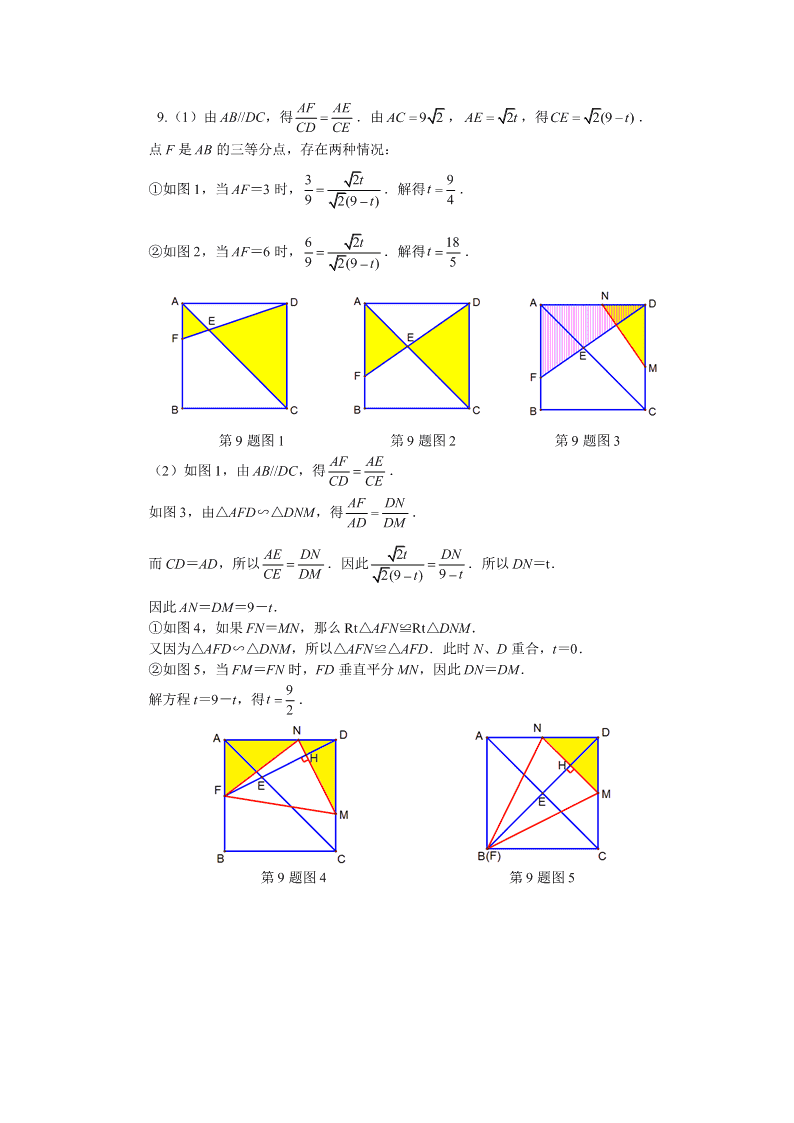
9．（ 2014 年杭州市拱墅区中考模拟第 22 题） 如图，在一个边长为 9cm 的正方形 ABCD 中，点 E、M 分别是线段 AC、CD 上的动点， 连结 DE 并延长交正方形的边于点 F，过点 M 作 MN⊥DF 于点 H，交 AD 于点 N．设点 M 从点 C 出发，以 1cm/s 的速度沿 CD 向点 D 运动；点 E 同时从点 A 出发，以 cm/s 速度 沿 AC 向点 C 运动，运动时间为 t（t＞0）． （1）当点 F 是 AB 的三等分点时，求出对应的时间 t； （2）当点 F 在 AB 边上时，连结 FN 、FM： ①是否存在 t 值，使 FN＝MN？若存在，请求出此时 t 的值；若不存在，请说明理由； ②是否存在 t 值，使 FN＝FM？若存在，请求出此时 t 的值；若不存在，请说明理由． 2 9.（1）由 AB//DC，得 AF AE CD CE ．由 92AC  ， 2AE t ，得 2(9 )CE t． 点 F 是 AB 的三等分点，存在两种情况： ①如图 1，当 AF＝3 时， 32 9 2(9 ) t t   ．解得 9 4t  ． ②如图 2，当 AF＝6 时， 62 9 2(9 ) t t   ．解得 18 5t  ． 第 9 题图 1 第 9 题图 2 第 9 题图 3 （2）如图 1，由 AB//DC，得 ． 如图 3，由△AFD∽△DNM，得 AF DN AD DM ． 而 CD＝AD，所以 AE DN CE DM ．因此 2 92(9 ) t DN tt   ．所以 DN＝t． 因此 AN＝DM＝9－t． ①如图 4，如果 FN＝MN，那么 Rt△AFN≌Rt△DNM． 又因为△AFD∽△DNM，所以△AFN≌△AFD．此时 N、D 重合，t＝0． ②如图 5，当 FM＝FN 时，FD 垂直平分 MN，因此 DN＝DM． 解方程 t＝9－t，得 9 2t  ． 第 9 题图 4 第 9 题图 5 10.（2014 年南京市雨花栖霞浦口化工园区四区联合模拟第 26 题） 已知二次函数 y＝mx2－5mx＋1（m 为常数，m＞0），设该函数图像与 y 轴交于点 A，图 像上一点 B 与点 A 关于该函数图像的对称轴对称． （1）求点 A、B 的坐标； （2）点 O 为坐标原点，点 M 为函数图像的对称轴上一动点，求当 M 运动到何处时 △MAO 的周长最小； （3）若该函数图像上存在点 P 与点 A、B 构成一个等腰三角形，且△PAB 的面积为 10， 求 m 的值． 10．（1）由 y＝mx2－5mx＋1，得 A(0, 1)，抛物线的对称轴为直线 5 2x  ． 所以点 B 的坐标为(5, 1)． （2）如图 1，当 M 运动到线段 OB 与对称轴的交点时，△MAO 的周长最小，这是因为： 如图 2，AO 为定值，MA＝MB，在△MOB 中，MO＋MB＞OB． 因此当 O、M、B 三点共线时，MB＋MO 最小． 如图 1，此时点 M 的坐标为 51( , )22 ，△MAO 的周长的最小值为 26 1 ． 第 10 题图 1 第 10 题图 2 第 10 题图 3 （3）因为△PAB 的面积为 10，AB＝5，所以 AB 边上的高为 4，即点 P 到 AB 的距离 PH 为 4． 等腰三角形 PAB 分三种情况： ①如图 3，当 PA＝PB 时，P 是抛物线的顶点，由于抛物线开口向上，此时 P 5( , 3)2  ． 将 P 代入 y＝mx2－5mx＋1，于是得到 16 25m  ． ②如图 4，当 AP＝AB 时，在 Rt△PAH 中，AP＝5，PH＝4，所以 AH＝3． 所以点 P 的坐标为(－3, 5)或(3,－3)． 将 P(－3, 5) 代入 y＝mx2－5mx＋1，于是得到 1 6m  ． 将 P(3,－3) 代入 y＝mx2－5mx＋1，于是得到 2 3m  ． ③如图 5，当 BP＝BA＝5 时，根据对称性，与情况②一样， 或 ． 第 10 题图 4 第 10 题图 5 4．如图，抛物线 y＝ax2＋bx－3 与 x 轴交于 A(1, 0)、B(3, 0)两点，与 y 轴交于点 D，顶 点为 C． （1）求此抛物线的解析式； （2）在 x 轴下方的抛物线上是否存在点 M，过 M 作 MN⊥x 轴于点 N，使以 A、M、N 为顶点的三角形与△BCD 相似？若存在，求出点 M 的坐标；若不存在，请说明理由． （1）因为抛物线 y＝ax2＋bx－3 与 x 轴交于 A(1, 0)、B(3, 0)两点， 所以 y＝a(x－1)(x－3)＝ax2－4ax＋3a． 所以 3a＝－3．解得 a＝－1． 所以抛物线的解析式为 y＝－x2＋4x－3． （2）由 y＝－x2＋4x－3＝－(x－2)2＋1，得 D(0,－3)，C(2, 1)． 如图 1，由 B(3, 0)、D(0,－3)、C(2, 1)，可知∠CBO＝45°，∠DBO＝45°． 所以∠CBD＝90°，且 21 332 BC BD ． 第 4 题图 1 第 4 题图 2 第 4 题图 3 因此△AMN 与△BCD 都是直角三角形，它们相似分 4 种情况讨论： ①当 3NA BD NM BC，且 M 在 A 右侧时， 1 3( 1)( 3) x xx   ． 解得 10 3x  ．此时 M 10 7( , )39 （如图 2）． ②当 ，且 M 在 A 左侧时， 1 3( 1)( 3) x xx   ． 解得 8 3x  ＞1，不符合题意（如图 3）． ③当 1 3 NA BC NM BD，且 M 在 A 右侧时， 11 ( 1)( 3) 3 x xx   ． 解得 x＝6．此时 M(6,－12)（如图 4）． ④当 ，且 M 在 A 左侧时， 11 ( 1)( 3) 3 x xx   ． 解得 x＝0．此时 M(0,－3)（如图 5）． 第 4 题图 4 第 4 题图 5 10．（2014 年南京市建邺区九年级学情调研卷第 26 题） 如图，在△ABC 中，AB＝AC＝4 2 ，BC＝8．⊙A 的半径为 2，动点 P 从点 B 出发沿 BC 方向以每秒 1 个单位的速度向点 C 运动，以点 P 为圆心，以 PB 为半径作⊙P，设点 P 运动的时间为 t 秒． （1）当⊙P 与直线 AC 相切时，求 t 的值； （2）当⊙P 与⊙A 相切时，求 t 的值； （3） 延长 BA 交⊙A 于点 D，连接 AP 交⊙A 于点 E，连接 DE 并延长交 BC 于点 F．当 △ABP 与△FBD 相似时，求 t 的值． 10．（1）在△ABC 中，已知 AB＝AC＝4 2，BC＝8，可知△ABC 是等腰直角三角形． 如图 1，过点 P 作 PM⊥AC，垂足为 M． 当⊙P 与直线 AC 相切时，PM＝PB＝t． 在 Rt△PCM 中，PM＝t，∠C＝45°，所以 PC＝ 2t ． 由 BC＝BP＋PC＝8，得 28tt．解得 8 2 8t ． 第 10 题图 1 第 10 题图 2 （2）如图 2，作 AH⊥BC，垂足为 H． 在 Rt△APH 中，AH＝4，PH＝|4－t|，所以 2 2 24 (4 ) 8 32AP t t t      ． 对于⊙A，r＝2；对于⊙P，R＝t；圆心距 d＝AP＝ 2 8 32tt ． ①当⊙P 与⊙A 外切时，由 R＋r＝d，得 22 8 32x t t    ．解得 7 3t  （如图 3）． ②当⊙P 与⊙A 内切时，由 R－r＝d，得 22 8 32t t t    ．解得 t＝7（如图 4）． 第 10 题图 3 第 10 题图 4 （3）△ABP 与△FBD 有公共角∠B，分两种情况讨论它们相似： ①如图 5，∠BAP＝∠D 是不可能的，这是因为∠BAP 是等腰三角形 ADE 的外角， ∠BAP＝2∠D． ②如图 6，当∠BPA＝∠D 时，在△ABP 中，∠BAP＝2∠BPA， 因此 45°＋3∠BPA＝180°．解得∠BPA＝45°． 此时△ABP 是等腰直角三角形，P 与 C 重合，所以 t＝8． 第 10 题图 5 第 10 题图 6