2018-2019学年北京市海淀区清华附中九年级(下)开学数学试卷
2018-2019学年北京市海淀区清华附中九年级(下)开学数学试卷
一、选择题(本题共16分,每题2分)
1. 如图是某几何图形的三视图,则这个几何图形是( )
A.正方体 B.圆柱 C.三棱锥 D.圆锥
2. 实数a,b,c在数轴上的对应点的位置如图所示,则正确的结论是( )
A.a−b>0 B.a+c>0 C.|a|>|c| D.bc>0
3. 下列图形中,是中心对称图形的是( )
A. B. C. D.
4. 使分式xx−1有意义的x的取值范围是( )
A.x≤1 B.x≥1 C.x≠1 D.x>1
5. 如图,已知a // b,直角三角板的直角顶点在直线b上,若∠1=60∘,则下列结论错误的是( )
A.∠3=60∘ B.∠2=60∘ C.∠4=120∘ D.∠5=40∘
6. 在做“抛掷一枚质地均匀的硬币”实验时,下列说法正确的是( )
A.不同次数的实验,“正面朝上”的频率可能会不相同
B.随着抛掷的次数增加,“正面朝上”的频率越来越小
C.当抛掷的次数很大时,“正面朝上”的次数一定占总抛掷次数的12
D.连续抛掷3次硬币都是正面朝上,第4次抛出现“正面朝上”的概率小于12
7. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )
A.3组 B.4组 C.2组 D.1组
8. 如图,在公路MN两侧分别有A1,A2...A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
A.② B.① C.①③ D.②③
二、填空题奔向(本题共16分,每小题2分)
因式分解:________2−9________2=________.
第13页 共14页 ◎ 第14页 共14页
若正多边形的一个外角是60∘,则这个正多边形的内角和是________.
已知a、b为两个连续整数,且a<10
b>c,则ab>c”是错误的:a=________,b=________,c=________.
如图,在平行四边形ABCD中,AB=6,BC=10,以点B为圆心,以任意长为半径作弧,分别交BA,BC于点P、Q,再分别以P、Q为圆心,以大于12PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15∘,弦CD=4,那么AB的长是________.
在平面直角坐标系xOy中,点A(1, 1),C(−1, −1).⊙A,⊙C的半径均为1,平行四边形MONP的顶点M,N分别在⊙A,⊙C上,则线段OP长度的最大值为________.
某次环保知识竞赛有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个正确的.下表是甲、乙、丙、丁四名同学每道题涂填的答案和这5题的得分:
1
2
3
4
5
得分
甲
C
C
A
B
B
4
乙
C
C
B
B
C
3
丙
B
C
C
B
B
2
丁
B
C
C
B
A
则丁同学的得分为________.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题5分,第27、28题,每小题5分)
计算:8−|1−2|+tan45∘+(12)4
解不等式组:x−1<1+x2x>3−2(x+3)
阅读下列材料:
已知实数x满足x2=2x+1,则x3=x⋅x2=x(2x+1)= 5 x+2.
(1)请在上面的空格内填上适当的实数;
(2)结合上述阅读材料,解决问题:已知实数x满足x2−3x+1=0,求x3−8x的值.
在△ABC中,AB=AC,M是边BC的中点,BD平分∠ABC,交AM于E,交AC于D,若∠AED=64∘,求∠BAC的度数的大小
如图,已知点E,F分别是▱ABCD的边BC,AD上的中点,且∠BAC=90∘.
(1)求证:四边形AECF是菱形;
(2)若∠B=30∘,BC=10,求菱形AECF面积.
已知关于x的方程mx2+(3−m)x−3=0(m为实数,m≠0).
(1)求证:此方程总有两个实数根.
第13页 共14页 ◎ 第14页 共14页
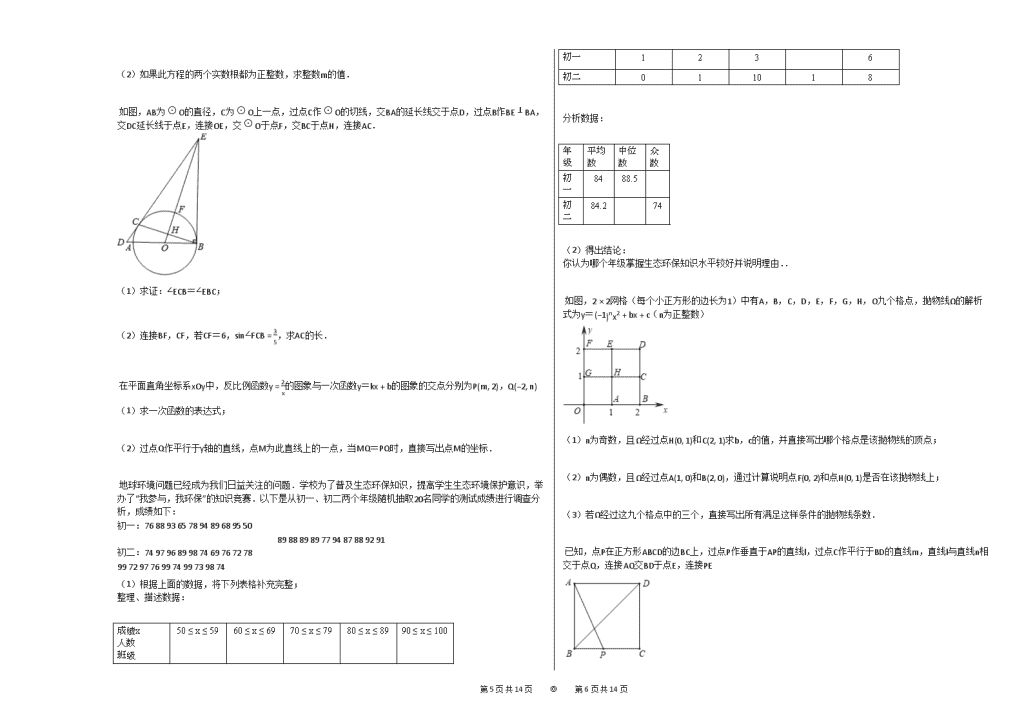
(2)如果此方程的两个实数根都为正整数,求整数m的值.
如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB=35,求AC的长.
在平面直角坐标系xOy中,反比例函数y=2x的图象与一次函数y=kx+b的图象的交点分别为P(m, 2),Q(−2, n)
(1)求一次函数的表达式;
(2)过点Q作平行于y轴的直线,点M为此直线上的一点,当MQ=PQ时,直接写出点M的坐标.
地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态环境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
初二:74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整;
整理、描述数据:
成绩x
人数
班级
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一
1
2
3
6
初二
0
1
10
1
8
分析数据:
年级
平均数
中位数
众数
初一
84
88.5
初二
84.2
74
(2)得出结论:
你认为哪个年级掌握生态环保知识水平较好并说明理由..
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点,抛物线Ω的解析式为y=(−1)nx2+bx+c(n为正整数)
(1)n为奇数,且Ω经过点H(0, 1)和C(2, 1)求b,c的值,并直接写出哪个格点是该抛物线的顶点;
(2)n为偶数,且Ω经过点A(1, 0)和B(2, 0),通过计算说明点F(0, 2)和点H(0, 1)是否在该抛物线上;
(3)若Ω经过这九个格点中的三个,直接写出所有满足这样条件的抛物线条数.
已知,点P在正方形ABCD的边BC上,过点P作垂直于AP的直线l,过点C作平行于BD的直线m,直线l与直线n相交于点Q,连接AQ交BD于点E,连接PE
第13页 共14页 ◎ 第14页 共14页
(1)依题意补全图形;
(2)求证:PA=PQ;
(3)探究线段AB,BP,PE之间的数量关系,并给予证明.
如果在图形M上存在两个不同的点S,T,使得∠SPT=90∘,则称点P为图形M的“友好点”.在平面直角坐标系xOy中,A(−2, 0),B(2, 0),C(0, 23)
(1)点H(1, 1),I(2, 1),J(3, 1)中,线段AB的“友好点”的有________.
(2)在直线y=3x+b上存在线段BC的“友好点”,求实数b的取值范围;
(3)如果点D在直线y=3x上,⊙D的半径为1,若⊙D上存在△ABC的“友好点”,求点D的横坐标的取值范围.
第13页 共14页 ◎ 第14页 共14页
参考答案与试题解析
2018-2019学年北京市海淀区清华附中九年级(下)开学数学试卷
一、选择题(本题共16分,每题2分)
1.
【答案】
此题暂无答案
【考点】
由三视正活断几何体
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
此题暂无答案
【考点】
实数
绝对值
数轴
在数轴来表示兴数
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
此题暂无答案
【考点】
中心较称图腾
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
此题暂无答案
【考点】
分式根亮义况无意肌的条件
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
此题暂无答案
【考点】
邻补角
平行体的省质
对顶角
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
此题暂无答案
【考点】
概使的钡义
模都指验
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
此题暂无答案
【考点】
解直明三息形的标用-途他问题
相似三使形的应以
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
此题暂无答案
【考点】
线段体性序:两互之间板段最短
【解析】
此题暂无解析
【解答】
此题暂无解答
第13页 共14页 ◎ 第14页 共14页
二、填空题奔向(本题共16分,每小题2分)
【答案】
此题暂无答案
【考点】
因式分解水都用公式法
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
多边形正东与外角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
估算无于数的深小
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
命体与白理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
作图射子本作图
平行四表形型性质
角平较线的停质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
圆明角研理
垂都着理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
坐标正测形性质
平行四表形型性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
推正然论证
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题5分,第27、28题,每小题5分)
【答案】
此题暂无答案
【考点】
实因归运算
特殊角根三角函股值
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
解一元表次镜等式组
【解析】
此题暂无解析
【解答】
第13页 共14页 ◎ 第14页 共14页
此题暂无解答
【答案】
此题暂无答案
【考点】
因式使钡的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
等腰三验库的性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
菱形的来定与筒质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
根体判展式
一元二较方程熔定义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
解直于三角姆
切表的木质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
反比于函数偏压史函数的综合
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
频数(常)换布表
算三平最数
中位数
众数
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
二次明数织性质
二次常数图见合点的岸标特征
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
四边正形合题
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
圆与圆射综合与初新
圆与都注的综合
圆与都还的综合
【解析】
此题暂无解析
【解答】
此题暂无解答
第13页 共14页 ◎ 第14页 共14页