数学函数导学案

数学函数导学案

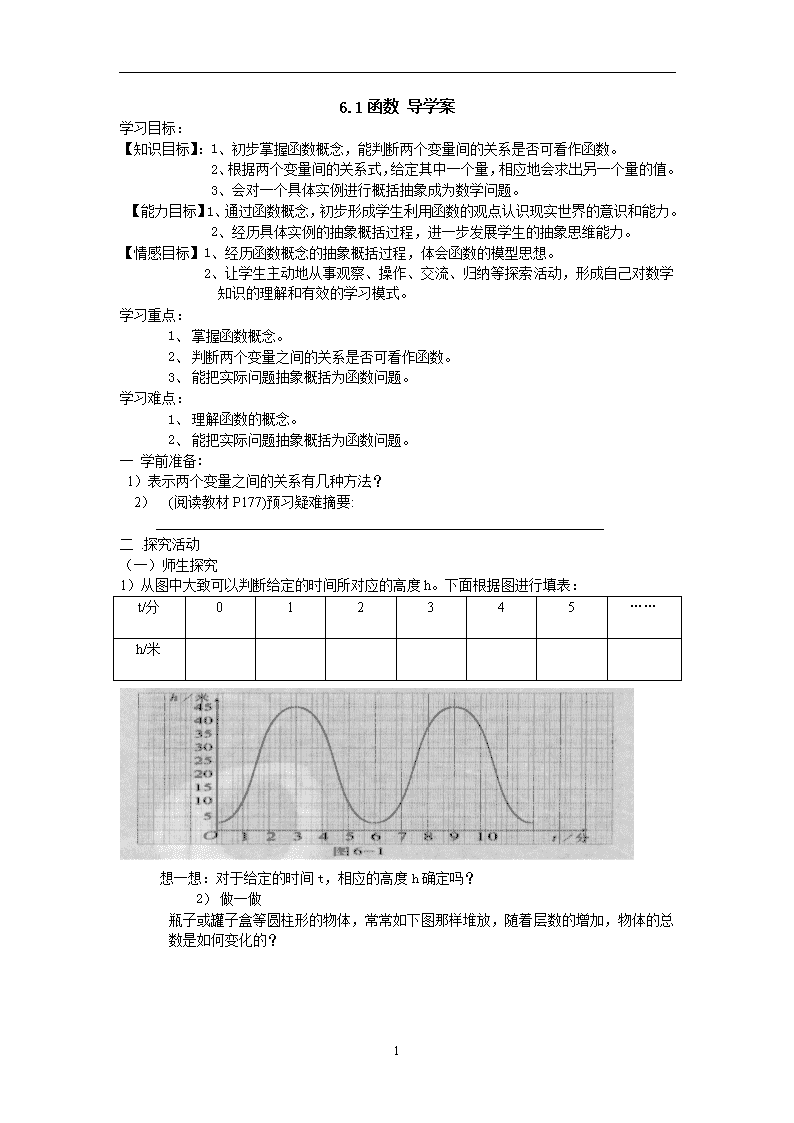
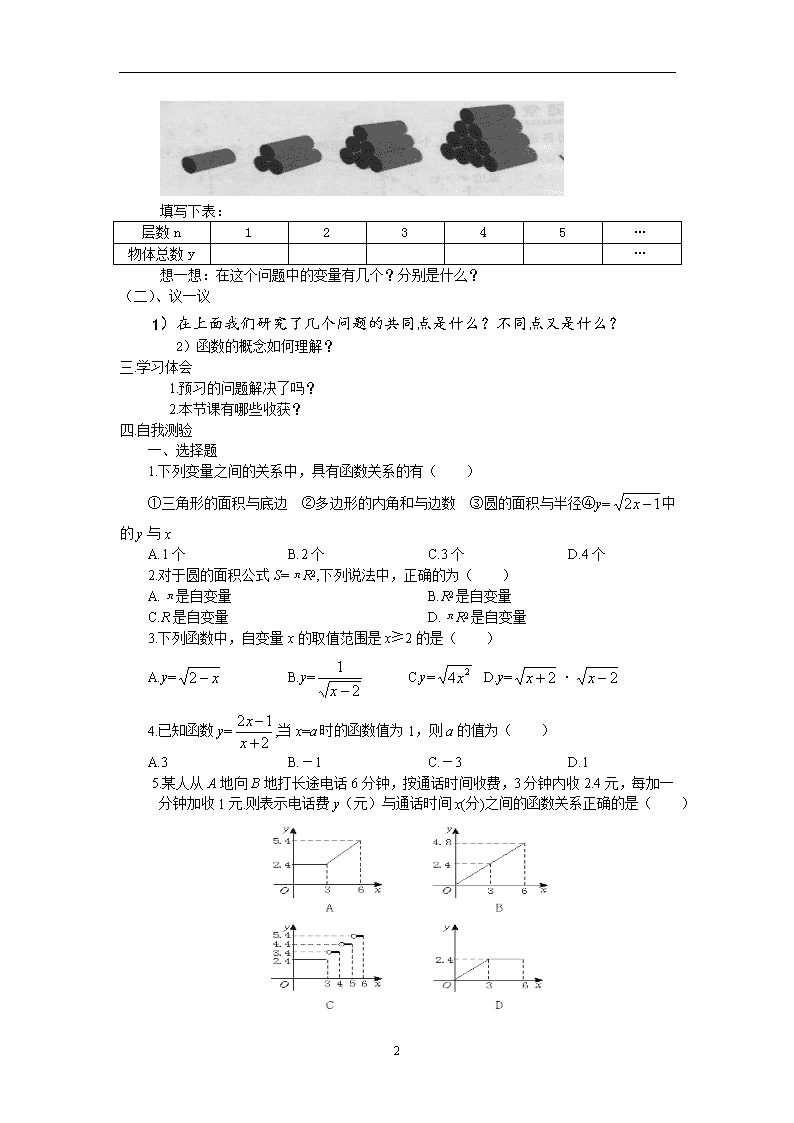
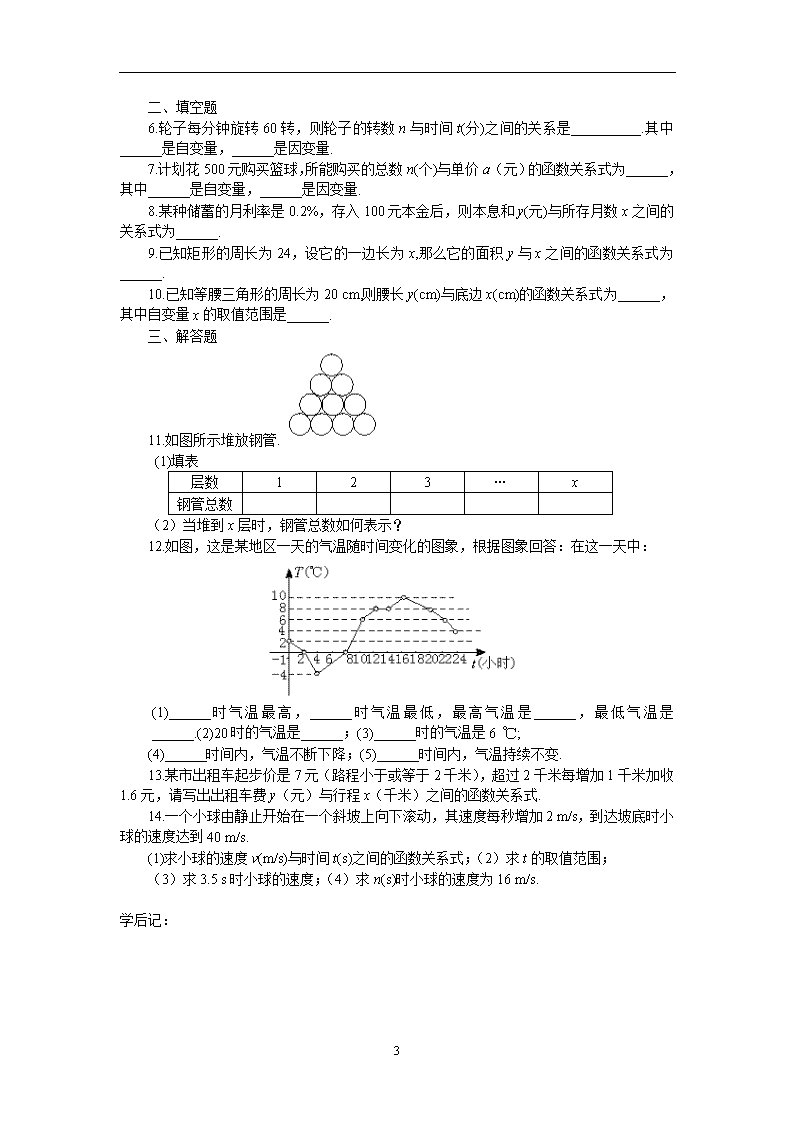
‎ ‎ ‎6.1函数 导学案 ‎ 学习目标：‎ ‎【知识目标】：1、初步掌握函数概念，能判断两个变量间的关系是否可看作函数。‎ ‎2、根据两个变量间的关系式，给定其中一个量，相应地会求出另一个量的值。‎ ‎3、会对一个具体实例进行概括抽象成为数学问题。‎ ‎ 【能力目标】1、通过函数概念，初步形成学生利用函数的观点认识现实世界的意识和能力。‎ ‎2、经历具体实例的抽象概括过程，进一步发展学生的抽象思维能力。‎ ‎【情感目标】1、经历函数概念的抽象概括过程，体会函数的模型思想。‎ ‎ 2、让学生主动地从事观察、操作、交流、归纳等探索活动，形成自己对数学知识的理解和有效的学习模式。‎ 学习重点：‎ 1、 掌握函数概念。‎ 2、 判断两个变量之间的关系是否可看作函数。‎ 3、 能把实际问题抽象概括为函数问题。‎ 学习难点：‎ 1、 理解函数的概念。‎ 2、 能把实际问题抽象概括为函数问题。‎ 一 学前准备:‎ ‎ 1）表示两个变量之间的关系有几种方法？‎ ‎2） (阅读教材P177)预习疑难摘要:‎ ‎________________________________________________________________‎ 二 .探究活动 ‎（一）师生探究 ‎1）从图中大致可以判断给定的时间所对应的高度h。下面根据图进行填表：‎ t/分 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎……‎ h/米 想一想：对于给定的时间t，相应的高度h确定吗？‎ 2） 做一做 瓶子或罐子盒等圆柱形的物体，常常如下图那样堆放，随着层数的增加，物体的总数是如何变化的？‎ 3‎ ‎ ‎ 填写下表：‎ 层数n ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎…‎ 物体总数y ‎…‎ 想一想：在这个问题中的变量有几个？分别是什么？‎ ‎（二）、议一议 ‎1）在上面我们研究了几个问题的共同点是什么？不同点又是什么？‎ ‎2）函数的概念如何理解？‎ 三.学习体会 ‎ 1.预习的问题解决了吗？ ‎ ‎2.本节课有哪些收获？‎ 四.自我测验 一、选择题 ‎1.下列变量之间的关系中，具有函数关系的有（ ）‎ ‎①三角形的面积与底边 ②多边形的内角和与边数 ③圆的面积与半径④y=中的y与x A.1个 B.2个 C.3个 D.4个 ‎2.对于圆的面积公式S=πR2,下列说法中，正确的为（ ）‎ A.π是自变量 B.R2是自变量 C.R是自变量 D.πR2是自变量 ‎3.下列函数中，自变量x的取值范围是x≥2的是（ ）‎ A.y= B.y= C.y= D.y=·‎ ‎4.已知函数y=,当x=a时的函数值为1，则a的值为（ ）‎ A.3 B.－1 C.－3 D.1‎ ‎5.某人从A地向B地打长途电话6分钟，按通话时间收费，3分钟内收2.4元，每加一分钟加收1元.则表示电话费y（元）与通话时间x(分)之间的函数关系正确的是（ ）‎ 3‎ ‎ ‎ 二、填空题 ‎6.轮子每分钟旋转60转，则轮子的转数n与时间t(分)之间的关系是__________.其中______是自变量，______是因变量.‎ ‎7.计划花500元购买篮球，所能购买的总数n(个)与单价a（元）的函数关系式为______，其中______是自变量，______是因变量.‎ ‎8.某种储蓄的月利率是0.2%，存入100元本金后，则本息和y(元)与所存月数x之间的关系式为______.‎ ‎9.已知矩形的周长为24，设它的一边长为x,那么它的面积y与x之间的函数关系式为______.‎ ‎10.已知等腰三角形的周长为20 cm,则腰长y(cm)与底边x(cm)的函数关系式为______，其中自变量x的取值范围是______.‎ 三、解答题 ‎11.如图所示堆放钢管.‎ ‎ (1)填表 层数 ‎1‎ ‎2‎ ‎3‎ ‎…‎ x 钢管总数 ‎（2）当堆到x层时，钢管总数如何表示？‎ ‎12.如图，这是某地区一天的气温随时间变化的图象，根据图象回答：在这一天中：‎ ‎(1)______时气温最高，______时气温最低，最高气温是______，最低气温是______.(2)20时的气温是______；(3)______时的气温是6 ℃;‎ ‎(4)______时间内，气温不断下降；(5)______时间内，气温持续不变.‎ ‎13.某市出租车起步价是7元（路程小于或等于2千米），超过2千米每增加1千米加收1.6元，请写出出租车费y（元）与行程x（千米）之间的函数关系式.‎ ‎14.一个小球由静止开始在一个斜坡上向下滚动，其速度每秒增加2 m/s，到达坡底时小球的速度达到40 m/s.‎ ‎(1)求小球的速度v(m/s)与时间t(s)之间的函数关系式；（2）求t的取值范围；‎ ‎（3）求3.5 s时小球的速度；（4）求n(s)时小球的速度为16 m/s.‎ 学后记：‎ 3‎