- 2021-05-20 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一 广东高考理科数学近家7年试题分类汇编
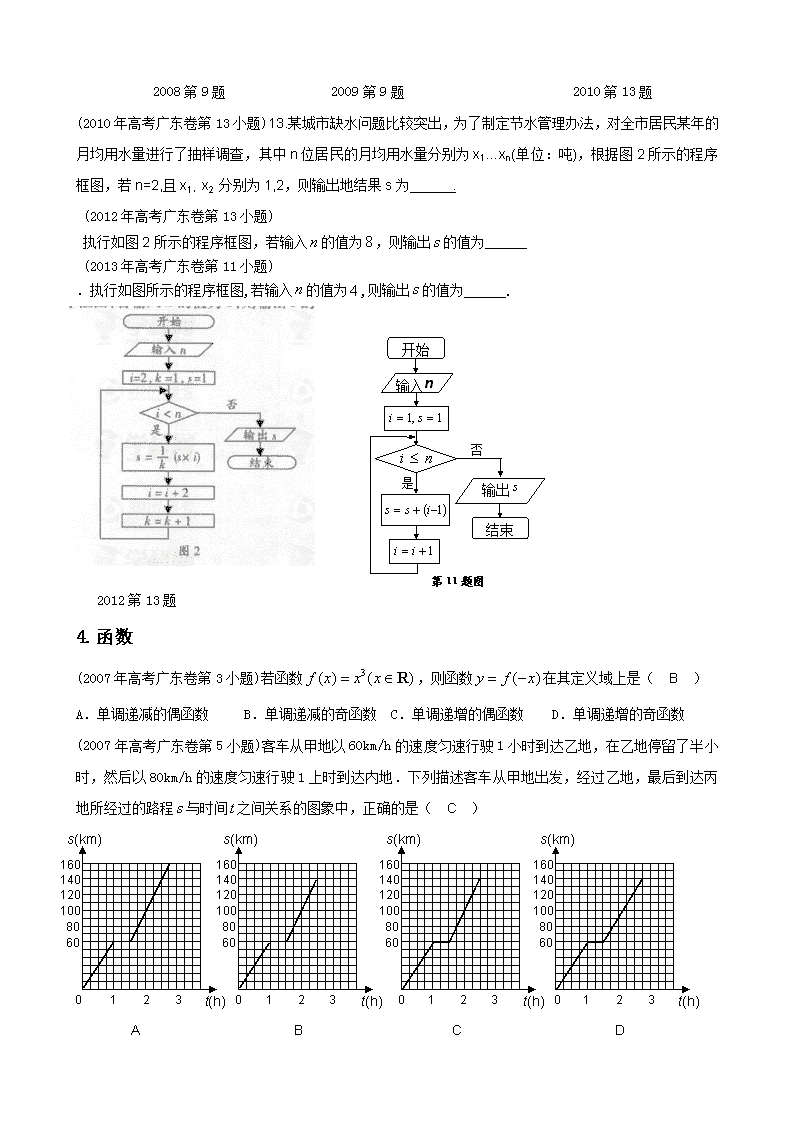
广东省高考理科数学近7年试题分类汇编(高一部分) 1.集合 (2007年高考广东卷第1小题) 已知函数的定义域为,的定义域为,则( ) A.{x |x>-1} B.{x|x<1} C.{x|-1<x<1} D. (2009年高考广东卷第1小题). 1. 已知全集,集合和的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有( ) A. 3个 B. 2个 C. 1个 D. 无穷多个 (2010年高考广东卷第1小题) 若集合A={-2<<1},B={0<<2}则集合A ∩ B=( ) A. {-1<<1} B. {-2<<1} C. {-2<<2} D. {0<<1} (2011年高考广东卷第2小题) 2.已知集合 ∣为实数,且,为实数,且,则的元素个数为( ) A.0 B.1 C.2 D.3 (2012年高考广东卷第2小题)设集合;则( ) (2013年高考广东卷第1小题)设集合,, 则( ) A . B. C. D. 2.向量 (2007年高考广东卷第10小题) 10. 若向量、满足||=||=1,与的夹角为,则 . (2008年高考广东卷第8小题) 8.在平行四边形中,与交于点是线段的中点,的延长线与交于点.若,,则( ) A. B. C. D. (2009年高考广东卷第10小题) 若平面向量,满足,平行于轴,,则 . w.w.w.k.s.5.u.c.o.m (2011年高考广东卷第3小题) ( ) A. B. C. D. (2012年高考广东卷第3小题) 若向量;则( ) 3.框图 (2007年高考广东卷第6小题)图l是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为、、…、(如表示身高(单位:)在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180(含160,不含180)的学生人数,那么在流程图中的判断框内应填写的条件是( ) A. B. C. D. (2008年高考广东卷第9小题) 9.阅读图3的程序框图,若输入,,则输出 , (注:框图中的赋值符号“”也可以写成“”或“”) (2009年高考广东卷第9小题) 开始 n整除a? 是 输入 结束 输出 图3 否 9. 随机抽取某产品件,测得其长度分别为,则图3所示的程序框图输出的 ,表示的样本的数字特征是 .(注:框图中的赋值符号“=”也可以写成“←”“:=”) 2008第9题 2009第9题 2010第13题 (2010年高考广东卷第13小题) 13.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1…xn(单位:吨),根据图2所示的程序框图,若n=2,且x1,x2 分别为1,2,则输出地结果s为 . (2012年高考广东卷第13小题) 执行如图2所示的程序框图,若输入的值为,则输出的值为 (2013年高考广东卷第11小题) .执行如图所示的程序框图,若输入的值为,则输出的值为______. 是 否 输入 输出 结束 开始 第11题图 n 2012第13题 4.函数 (2007年高考广东卷第3小题)若函数,则函数在其定义域上是( B ) A.单调递减的偶函数 B.单调递减的奇函数 C.单调递增的偶函数 D.单调递增的奇函数 (2007年高考广东卷第5小题)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1上时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程与时间之间关系的图象中,正确的是( C ) 1 2 3 60 80 100 120 140 160 t(h) s(km) 1 2 3 60 80 100 120 140 160 t(h) s(km) 1 2 3 60 80 100 120 140 160 t(h) s(km) 1 2 3 60 80 100 120 140 160 t(h) s(km) A. B. C. D. 0 0 0 0 (2009年高考广东卷第4小题)若函数是函数的反函数,且, 则 ( ) A. B. C. D.2 (2010年高考广东卷第3小题)若函数与的定义域均为,则( ) A.与均为偶函数 B.为奇函数,为偶函数 C.与均为奇函数 D.为偶函数,为奇函数 (2011年高考广东卷第4小题)函数的定义域是( ) A. B. C. D. (2011年高考广东卷第12小题)设函数 . (2012年高考广东卷第4小题)下列函数中,在区间上为增函数的是( ) (2013年高考广东卷第2小题)定义域为的四个函数,,,中, 奇函数的个数是( ) A . B. C. D. (2007年高考广东卷第20小题)已知是实数,函数,如果函数在区间上有零点,求的取值范围. (2010年高考广东卷第20小题)已知函数对任意实数均有,其中常数为负数,且在区间上有表达式.w_w w. k#s5_u.c o*m (1)求,的值; (2)写出在上的表达式,并讨论函数在上的单调性; (3)求出在上的最小值与最大值,并求出相应的自变量的取值. w_w*w.k_s_ 5.三角函数 (2007年高考广东卷第3小题) 若函数(),则是( ) A.最小正周期为的奇函数 B. 最小正周期为的奇函数 C.最小正周期为的偶函数 D. 最小正周期为的偶函数 (2008年高考广东卷第12小题) 已知函数,,则的最小正周期是 . (2008年高考广东卷第16小题) 16.(本小题满分13分) 已知函数,的最大值是1,其图像经过点. (1)求的解析式;(2)已知,且,,求的值. (2009年高考广东卷第16小题)16.(本小题满分12分) 已知向量与互相垂直,其中. (1)求和的值; (2)若,求的值.w.w.w.k.s.5.u.c.o.m . w_w w. k#s5_u.c o*m.s.5.u.c.o.m (2010年高考广东卷第16小题) 16、(本小题满分14分) 已知函数在时取得最大值4. (1) 求的最小正周期; (2) 求的解析式; (3) 若(α +)=,求sinα. (2011年高考广东卷第16小题) 已知函数 (1)求的值; (2) 设求的值. (2012年高考广东卷第16小题) (本小题满分12分) 已知函数的最小正周期为 (1)求的值; (2)设,;求的值 (2013年高考广东卷第16小题)(本小题满分12分) 已知函数,. (Ⅰ) 求的值; (Ⅱ) 若,,求. 6.概率统计 (2008年高考广东卷第3小题) 3.某校共有学生2000名,各年级男、女生人数如表1.已知在全校 学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( ) 一年级 二年级 三年级 女生 373 男生 377 370 A.24 B.18 C.16 D.12 表1 (2011年高考广东卷第6小题) 6. 甲、乙两队进行排球决赛,现在的情形是甲队只要在赢一次就获冠军,乙队需要再赢两局才能得冠军,若两队胜每局的概率相同,则甲队获得冠军的概率为( ) A. B. C. D. (2011年高考广东卷第13小题) 13. 某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm .因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为_____cm. (2012年高考广东卷第7小题) 7. 从个位数与十位数之和为奇数的两位数中任取一个,其个位数为的概率是( ) (2007年高考广东卷第17小题) 17.(本小题满分12分) 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生 产能耗 (吨标准煤)的几组对照数据 (1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性 回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值: (2013年高考广东卷第17小题) (本小题满分12分) 第17题图 某车间共有名工人,随机抽取名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. (Ⅰ) 根据茎叶图计算样本均值; (Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人. 根据茎叶图推断该车间名工人中有几名优秀工人; (Ⅲ) 从该车间名工人中,任取人,求恰有名优秀工人的概率. 7.立体几何 (2008年高考广东卷第5小题) 将正三棱柱截去三个角(如图1所示分别是三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( ) E F D I A H G B C E F D A B C 侧视 图1 图2 B E A. B E B. B E C. B E D. (2009年高考广东卷第5小题) ①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;w.w.w.k.s.5.u.c.o.m ④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是( )w.w.w.k.s.5.u.c.o.m A. ①和② B. ②和③ C. ③和④ D. ②和④ (2010年高考广东卷第6小题) 如图1,△ ABC为三角形,// // , ⊥平面ABC 且3== =AB,则多面体△ABC -的正视图(也称主视图)是( ) (2011年高考广东卷第7小题) 正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱的对角线条数共有( ) A.20 B.15 C.12 D. 10 (2011年高考广东卷第7小题) 如图1-3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为( ) A. B. C. D. (2012年高考广东卷第6小题) 某几何体的三视图如图1所示,它的体积为( ) 正视图 俯视图 侧视图 第5题图 (2013年高考广东卷第5小题) 5.某四棱台的三视图如图所示,则该四棱台的体积是 ( ) A . B. C. D. (2013年高考广东卷第6小题) 6.设是两条不同的直线,是两个不同的平面,下列命题中正确的是( ) A . 若,,,则 B.若,,,则 C.若,,,则 D.若,,,则 (2012年高考广东卷第18小题) (本小题满分13分) 如图所示,在四棱锥中,底面为矩形, 平面,点在线段上,平面。 (1) 证明:平面; (2) 若,求二面角的正切值; (2013年高考广东卷第18小题) (本小题满分14分) 如图1,在等腰直角三角形中,,,分别是上的点,, . C O B D E A C D O B E 图1 图2 为的中点.将沿折起,得到如图2所示的四棱锥,其中. (Ⅰ) 证明:平面; (Ⅱ) 求二面角的平面角的余弦值. 8.直线方程与圆的方程 (2008年高考广东卷第11小题) 经过圆的圆心,且与直线垂直的直线方程是 . (2010年高考广东卷第12小题) 已知圆心在x轴上,半径为的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是 9.新题型 图3 (2007年高考广东卷第10小题) 图3是某汽车维修公司的维修点环形分布图.公司在年初分配给四个维修点某种配件各50件.在使用前发现需将四个维修点的这批配件分别调整为,,,件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(件配件从一个维修点调整到相邻维修点的调动件次为)为( ) A. B. C. D. (2009年高考广东卷第10小题)广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表.若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短路线距离是( ) A. B.21 C.22 D.23 w.w.w.k.s.5.u.c.o.m (2010年高考广东卷第10小题) 在集合{a,b,c,d}上定义两种运算和如下:w_w w. k#s5_u.c o*m 那么d ( ) A.a B.b C.c D.d (2011年高考广东卷第10小题)设是上的任意实值函数,如下定义两个函数对任意则下列等式恒成立的是( ) A. B. C. D. (2012年高考广东卷第8小题)8. .对任意两个非零的平面向量和,定义;若平面向量满足,与的夹角,且都在集合中,则( ) (2013年高考广东卷第8小题)8.设整数,集合.令集合 若和都在中,则下列选项正确的是( ) A . , B., C., D., 查看更多