- 2021-05-20 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】河南省商丘市回民中学2019-2020学年高一上学期期中联考试卷
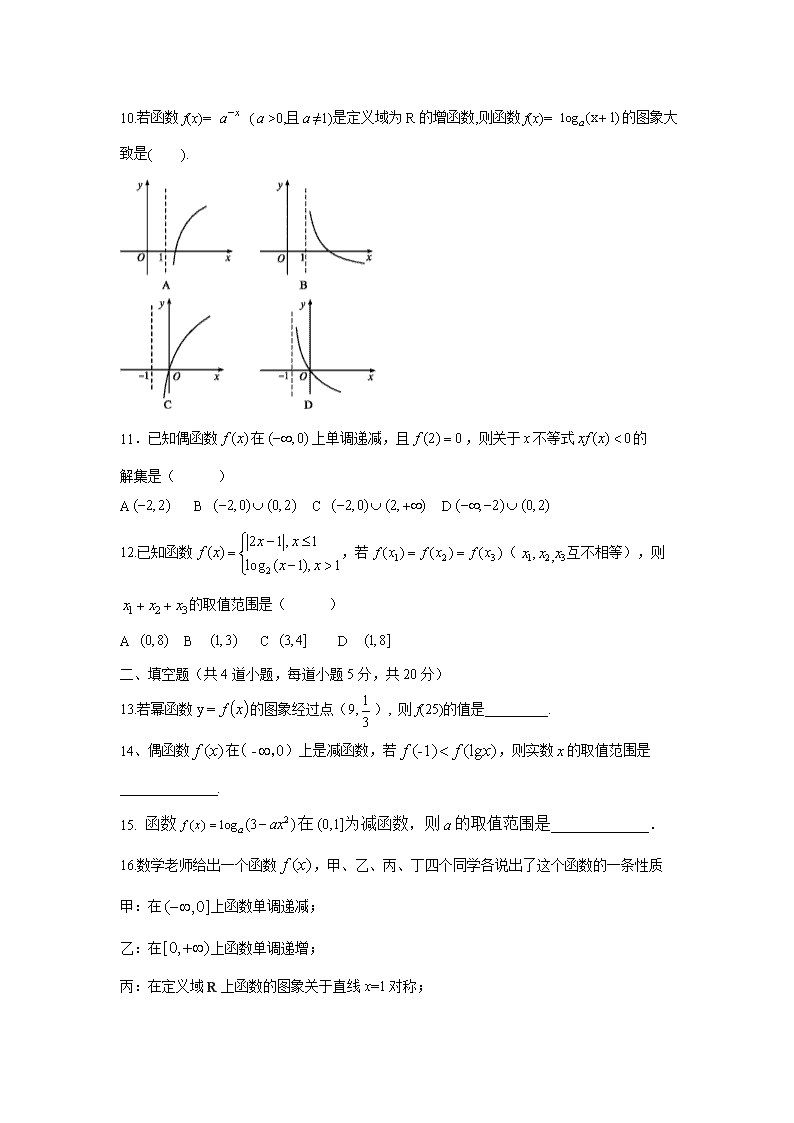
www.ks5u.com 河南省商丘市回民中学2019-2020学年高一上学期期中 联考数学试卷 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.函数的定义域为( ) A B C D 2.已知集合A=B=R,x∈A,y∈B,f:x→y=ax+b,若4和10的原象分别对应是6和9,则19在f作用下的象为( ) A 18 B 30 C D 28 3.已知f(x)是一次函数,且2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)的解析式为 A 2x+3 B 3x+2 C 3x-2 D 2x-3 4.三个数之间的大小关系是( ) A B C D 5.已知2lg(x-2y)=lgx+lgy,则的值为( ) A 1 B 4 C 1或4 D 或4 6. 方程在下列哪个区间必有实数解( ) A (1,2) B (2,3) C (3,4) D (4,5) 7.已知,则( ) A 3 B 6 C 10 D 12 8.已知定义域为R的函数f(x)在区间(-∞,5)上单调递减,对任意实数t,都有 f(5+t)=f(5-t),那么下列式子一定成立的是( ) A f(-1)<f(9)<f(13) B f(13)<f(9)<f(-1) C f(13)<f(-1)<f(9) D f(9)<f(-1)<f(13) 9.设f(x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-2)等于( ). A -7 B -3 C 7 D 3 10.若函数f(x)= (>0,且≠1)是定义域为R的增函数,则函数f(x)= 的图象大致是( ). 11.已知偶函数在上单调递减,且,则关于不等式的 解集是( ) A B C D 12.已知函数,若(互不相等),则的取值范围是( ) A B C D 二、填空题(共4道小题,每道小题5分,共20分) 13.若幂函数y =的图象经过点(9,), 则f(25)的值是_________. 14、偶函数在)上是减函数,若,则实数的取值范围是______________. 15. 函数在为减函数,则的取值范围是______________. 16.数学老师给出一个函数,甲、乙、丙、丁四个同学各说出了这个函数的一条性质 甲:在上函数单调递减; 乙:在上函数单调递增; 丙:在定义域R上函数的图象关于直线x=1对称; 丁:不是函数的最小值. 老师说:你们四个同学中恰好有三个人说的正确. 那么,你认为_________说的是错误 三、解答题(本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤) 17.(每题5分,共10分)求下列各式的值 ⑴ (2) 18.(12分)已知集合A=,B={x|2查看更多