- 2021-05-20 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学几何证明题题型分析
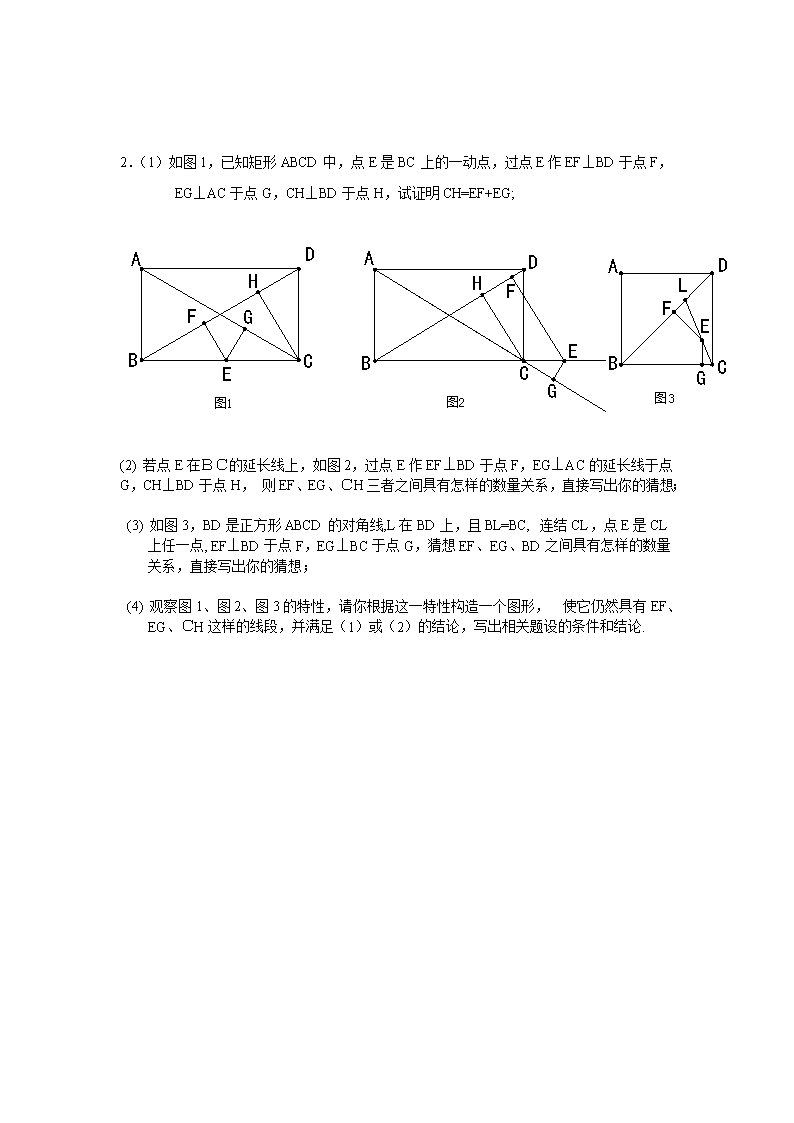
中考数学经典几何证明题(一) 1.(1)如图1所示,在四边形中,=,与相交于点,分别是的中点,联结,分别交、于点,试判断的形状,并加以证明; (2)如图2,在四边形中,若,分别是的中点,联结FE并延长,分别与的延长线交于点,请在图2中画图并观察,图中是否有相等的角,若有,请直接写出结论: ; (3)如图3,在中,,点在上,,分别是的中点,联结并延长,与的延长线交于点,若,判断点与以AD为直径的圆的位置关系,并简要说明理由. 图 1 图2 图3 2.(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,试证明CH=EF+EG; (2) 若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H, 则EF、EG、CH三者之间具有怎样的数量关系,直接写出你的猜想; (3) 如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC, 连结CL,点E是CL上任一点, EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想; (4) 观察图1、图2、图3的特性,请你根据这一特性构造一个图形, 使它仍然具有EF、EG、CH这样的线段,并满足(1)或(2)的结论,写出相关题设的条件和结论. 3. 如图,△ABC是等边三角形,F是AC的中点,D在线段BC上,连接DF,以DF为边在DF的右侧作等边△DFE,ED的延长线交AB于H,连接EC,则以下结论:①∠AHE+∠AFD=180°;②AF=BC;③当D在线段BC上(不与B,C重合)运动,其他条件不变时是定值;④当D在线段BC上(不与B,C重合)运动,其他条件不变时是定值; (1)其中正确的是-------------------; (2)对于(1)中的结论加以说明; 4. 在中,AC=BC,,点D为AC的中点. (1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作,交直线AB于点H.判断FH与FC的数量关系并加以证明. (2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明. 5. 如图12,在△ABC中,D为BC的中点,点E、F分别在边AC、AB上,并且∠ABE=∠ACF,BE、CF交于点O.过点O作OP⊥AC,OQ⊥AB,P、Q为垂足.求证:DP=DQ. 6. 如图。,BD是△ABC的内角平分线,CE是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G。 探究:线段FG的长与△ABC三边的关系,并加以证明。 说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明。 注意:选取①完成证明得10分;选取②完成证明得7分。 ①可画出将△ADF沿BD折叠后的图形; ②将CE变为△ABC的内角平分线。(如图2) 附加题:探究BD、CE满足什么条件时,线段FG的长与△ABC的周长存在一定的数量关系,并给出证明。 7. 在四边形ABCD中,对角线AC平分∠DAB. (1)如图①,当∠DAB=120°,∠B=∠D=90°时,求证:AB+AD=AC. (2)如图②,当∠DAB=120°,∠B与∠D互补时,线段AB、AD、AC有怎样的数量关系?写出你的猜想,并给予证明. (3)如图③,当∠DAB=90°,∠B与∠D互补时,线段AB、AD、AC有怎样的数量关系?写出你的猜想,并给予证明. 8. 设点E是平行四边形ABCD的边AB的中点,F是BC边上一点,线段DE和AF相交于点P,点Q在线段DE上,且AQ∥PC. (1)证明:PC=2AQ. (2)当点F为BC的中点时,试比较△PFC和梯形APCQ面积的大小关系,并对你的结论加以证明. 9. 两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB =∠DCE = 90°,F是DE的中点,H是AE的中点,G是BD的中点. (1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为_______和位置关系为______; (2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由; (2)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明. A B D E C H F G 图3 A B D E C H F G 图1 图2 A B D E C H F G 10. 已知△ABC中,AB=AC=3,∠BAC=90°,点D为BC上一点,把一个足够大的直角三角板的直角顶点放在D处. (1)如图①,若BD=CD,将三角板绕点D逆时针旋转,两条直角边分别交AB、AC于点E、点F,求出重叠部分AEDF的面积(直接写出结果). (2)如图②,若BD=CD,将三角板绕点D逆时针旋转,使一条直角边交AB于点E、另一条直角边交AB的延长线于点F,设AE=x,重叠部分的面积为y,求出y与x的函数关系式,并写出自变量x的取值范围. (3)若BD=2CD,将三角板绕点D逆时针旋转,使一条直角边交AC于点F、另一条直角边交射线AB于点E.设CF=x(x>1),重叠部分的面积为y,求出y与x的函数关系式,并写出自变量x的取值范围. 中考几何经典证明题(二) 1、如图,△ABC中,∠BAC=90°,AD⊥BC,E为CB延长线上一点,且∠EAB=∠BAD,设DC=kBD,试探究EC与EA的数量关系。 2、如图,△ABC中,∠BAC=90°,AD⊥BC,DE⊥AB,DF⊥AC,若AB=kAC,试探究BE与CF的数量关系。 3、如图,在△ABC和△PQD中,AC=kBC,DP=kDQ,∠C=∠PDQ,D、E分别是AB、AC的中点,点P在直线BC上,连接EQ交PC于点H。猜想线段EH与AC的数量关系,并证明你的猜想,若证明有困难,则可选k=1证明之。 4、在△ABC中,O是AC上一点,P、Q分别是AB、BC上一点,∠B=45°,∠POQ=135°,BC=kAB,OC=mAO。试说明OP与OQ是数量关系,选择条件:(1)m=1,(2)m=k=1。 5、如图,△ABC中,AD是BC边上的中线,∠CAD=∠B,AC=kAB,E在AD延长线上, ∠CED=∠ADB,探究AE与AD的关系。 6、如图,∠BAC=90°,AD⊥BC,DE⊥AB, AB=kAC,探究BE与AE是数量关系。查看更多