【物理】2019届二轮复习功率学案（全国通用）

【物理】2019届二轮复习功率学案（全国通用）

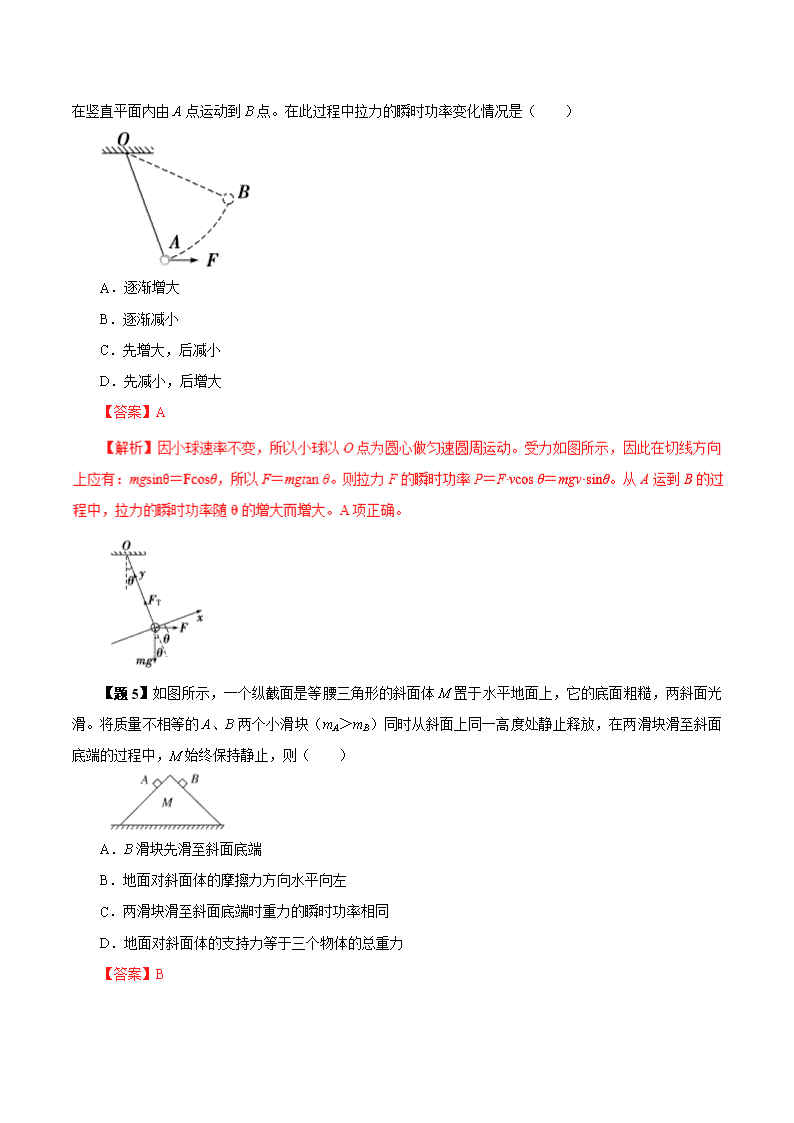
一、功率 ‎1．定义：功与完成这些功所用时间的比值。‎ ‎2．物理意义：标量，描述力对物体做功的快慢。只有正值，没有负值。‎ ‎3．定义式：P＝，P为时间t内的平均功率。‎ ‎4．单位：国际单位是瓦特，符号是w，常用的单位还有kw。‎ ‎【题1】关于功率的概念，以下说法正确的是（ ）‎ A．功率是描述力对物体做功多少的物理量 B．由P＝W/t可知，功率与时间成反比 C．由P＝Fv可知只要F不为零，v也不为零，那么功率P就一定不为零 D．某个力对物体做功越快，它的功率就一定大 ‎【答案】D 二、平均功率和瞬时功率 ‎1．平均功率 ‎（1）定义：在某一段时间内或某一过程的功率。‎ ‎（2）意义：反映物体在某一段时间内做功的快慢。‎ ‎（3）计算：①利用＝。‎ ‎②利用＝Fcos α，其中为物体运动的平均速度。‎ ‎【题2】（多选）我国 学家正在研制航母舰载机使用的电磁弹射器。舰载机总质量为3.0×104 kg，设起飞过程中发动机的推力恒为1.0×105 N；弹射器有效作用长度为100 m，推力恒定。要求舰载机在水平弹射结束时速度大小达到80 m/s。弹射过程中舰载机所受总推力为弹射器和发动机推力之和，假设所受阻力为总推力的20 ，则（ ）‎ A．弹射器的推力大小为1.1×106 N B．弹射器对舰载机所做的功为1.1×108 J C．弹射器对舰载机做功的平均功率为8.8×107 W D．舰载机在弹射过程中的加速度大小为32 m/s2‎ ‎【答案】ABD　‎ ‎【解析】对舰载机应用运动学公式v2－0＝2ax，代入数据得加速度a＝32 m/s2，D正确；设总推力为F，对舰载机应用牛顿第二定律可知：F－20 F＝ma，得F＝1.2×106 N，而发动机的推力为1.0×105 N，则弹射器的推力为F推＝（1.2×106－1.0×105）N＝1.1×106 N，A正确；弹射器对舰载机所做的功为W＝F推·l＝1.1×108 J，B正确；弹射过程所用的时间为t＝＝ s＝2.5 s，平均功率P＝＝ W＝4.4×107 W，C错误。‎ ‎【题3】（多选）如图甲所示，物体受到水平推力F的作用，在粗糙水平面上做直线运动。通过力传感器和速度传感器监测到推力F、物体的速度v随时间t变化的规律如图乙所示。取g＝10 m/s2。则（ ）‎ A．物体的质量m＝1.0 kg B．物体与水平面间的动摩擦因数μ＝0.20‎ C．第2 s内物体克服摩擦力做的功W＝2.0 J D．前2 s内推力F做功的平均功率P＝1.5 W ‎【答案】CD ‎2．瞬时功率 ‎（1）定义：在某一时刻或某一位置时的功率。‎ ‎（2）意义：反映物体在某一时刻做功的快慢。‎ ‎（3）计算：‎ ‎①利用公式P＝Fvcos α，其中v为t时刻的瞬时速度。‎ ‎②P＝FvF，其中vF为物体的速度v在力F方向上的分速度。‎ ‎③P＝Fvv，其中Fv为物体受到的外力F在速度v方向上的分力。‎ ‎【题4】如图所示，细线的一端固定于O 点，另一端系一小球。在水平拉力作用下，小球以恒定速率在竖直平面内由A点运动到B点。在此过程中拉力的瞬时功率变化情况是（ ）‎ A．逐渐增大 B．逐渐减小| |k ]‎ C．先增大，后减小 ‎ D．先减小，后增大 ‎【答案】A ‎【题5】如图所示，一个纵截面是等腰三角形的斜面体M置于水平地面上，它的底面粗糙，两斜面光滑。将质量不相等的A、B两个小滑块（mA＞mB）同时从斜面上同一高度处静止释放，在两滑块滑至斜面底端的过程中，M始终保持静止，则（ ）‎ A．B滑块先滑至斜面底端 B．地面对斜面体的摩擦力方向水平向左 C．两滑块滑至斜面底端时重力的瞬时功率相同 D．地面对斜面体的支持力等于三个物体的总重力 ‎【答案】B　‎ ‎3．计算功率的基本思路 ‎（1）首先判断待求的功率是瞬时功率还是平均功率。‎ ‎（2）平均功率与一段时间（或过程）相对应，计算时应明确是哪个力在哪段时间（或过程）内做功的平均功率。‎ ‎（3）瞬时功率计算时应明确是哪个力在哪个时刻（或状态）的功率。求解瞬时功率时，如果F与v不同向，可用力F乘以F方向的分速度，或速度v乘以速度方向的分力求解。‎ ‎【题6】（多选）质量为m的物体静止在光滑水平面上，从t＝0时刻开始受到水平力的作用。力F的大小与时间t的关系如图所示，力的方向保持不变，则（ ）‎ A．3t0时刻的瞬时功率为 ‎ B．3t0时刻的瞬时功率为 C．在t＝0到3t0这段时间内，水平力的平均功率为 D．在t＝0时3t0这段时间内，水平力的平均功率为 ‎【答案】BD ‎【解析】物体在0 2t0和2t0 3t0内都做匀加速直线运动，但加速度大小不相同。‎ 在0 3t0时间内力F是变力，应使用＝求平均功率。‎ 根据F－t图线，在0 2t0时间内的加速度a1＝ ‎2t0时刻的速度v2＝a1·2t0＝t0‎ ‎0 2t0内位移x1＝·2t0＝t，故F0做的功W1＝F0x1＝t 故3F0做的功W2＝3F0·x2＝ 学, , ,X,X,K]‎ 因此在0 3t0时间内的平均功率P＝＝，故B、D正确。学 ‎ ‎【题7】质量为m的物体，从倾角为θ的光滑斜面顶端由静止而下滑。求：‎ （1） 前n秒内重力对物体做功的平均功率；‎ ‎（2）第n秒内重力对物体做功的平均功率； 学+ + ]‎ ‎（3）第n秒末重力对物体做功的瞬时功率。‎ ‎（1）前n秒内重力对物体做功的平均功率n=WG/t=mgsn sinθ/t=mng2sin2θ ‎（2）第n秒内重力的平均功率=mg〔ngsinθ+（n–1）gsinθ〕sinθ/2=（n－）mg2sin2θ ‎（3）第n秒末重力对物体做功的瞬时功率Pn=mgvnsinθ=mng2sin2θ 说明：求平均功率用P=W/t和P=Fcosθ（其中θ是F与v的夹角，F为恒力）。求瞬时功率一般用P=Fvcosθ（其中F、v、θ均为此时的瞬时值）。‎ ‎【题8】如图所示，水平传送带正以v＝2 m/s的速度运行，两端水平距离l＝8 m，把一质量m＝2 kg的物块轻轻放到传送带的A端，物块在传送带的带动下向右运动，若物块与传送带间的动摩擦因数μ＝0.1，不计物块的大小，g取10 m/s2，则把这个物块从A端传送到B端的过程中，‎ ‎（1）摩擦力对物块做功的平均功率是多少？ 学 ]‎ ‎（2）1 s时，摩擦力对物块做功的功率是多少？‎ ‎（3）1 s时，皮带克服摩擦力做功的功率是多少？‎ ‎【答案】（1）0.8 W （2）2 W　（3）4 W 物块受向右的摩擦力为：Ff＝μmg＝0.1×2×10 N＝2 N 加速度为a＝＝μg＝0.1×10 m/s2＝1 m/s2‎ 当物块与传送带相对静止时，物块的位移为：x＝＝ m＝2 m。‎ 摩擦力做功为：W＝Ffx＝2×2 J＝4 J 相对静止后物块与传送带之间无摩擦力，此后物块匀速运动到B端，物块由A端运动到B端所用的时间为：t＝＋＝ s＋ s＝5 s 则物块在被传送过程中所受摩擦力的平均功率为：＝＝ W＝0.8 W。‎ ‎（2）1 s时，物块的速度为v1＝at＝1 m/s 则摩擦力对物块做功的功率为P1＝Ffv1＝2×1 W＝2 W。‎ ‎（3）皮带的速度为v＝2 m/s，故皮带克服摩擦力做功的功率为P2＝Ffv＝2×2 W＝4 W。学 ‎ 三、额定功率和实际功率 ‎1．额定功率 ‎（1）定义：发动机正常条件下长时间工作时的最大功率。‎ ‎（2）特点：不同机械额定功率可能不同，但同一机械额定功率不变。‎ ‎2．实际功率：‎ ‎（1）机械实际工作时输出的功率。要求小于或等于额定功率。‎ ‎（2）同一机械实际功率随工作情况而变。‎ ‎3．功率与速度——公式P=Fv的运用有三种情况 ‎（1）当F一定时，物体的运动速度越大，功率P也越大。汽车在高速路上，加大油门增大输出功率，可以提高速度。‎ ‎（2）当v一定时，F与P成正比，F越大，P越大。汽车上坡时，要使速度不变，应加大油门，增大输出功率，获得较大牵引力。‎ ‎（3）当P一定时，F与v成反比，如汽车在额定功率下行驶，要增大牵引力，则必须降低行驶速度；反之则必须减小牵引力。‎ ‎【题9】某汽车在平直公路上以功率 P、速度v0匀速行驶时，牵引力为 F0。在 t1‎ 时刻，司机减小油门，使汽车的功率减为，此后保持该功率继续行驶，t2时刻，汽车又恢复到匀速运动状态。下面是有关汽车牵引力 F、速度 v的几种说法，其中正确的是（ ）‎ A．t2后的牵引力仍为 F0‎ B．t2后的牵引力小于 F0‎ C．t2后的速度仍为 v0‎ D．t2后的速度小于 v0‎ ‎【答案】AD　‎ 二、机车的启动 ‎1．以恒定功率起动 ]‎ 汽车从静止开始以额定功率起动，开始时由于汽车的速度很小，由公式P=Fv知：牵引力F较大，因而由牛顿第二定律F–f=ma知，汽车的加速度较大。随着时间的推移，汽车的速度将不断增大，牵引力F将减小，加速度减小，但是由于速度方向和加速度方向相同，汽车的速度仍在不断增大，牵引力将继续减小，直至汽车的牵引力F和阻力f相平衡为止。汽车的牵引力F和阻力f平衡时，F–f=0，加速度a＝0，汽车的速度达到最大值vm。汽车的运动形式是做加速度越来越小的变加速直线运动，最终做匀速直线运动，其速度–时间图像如图所示。‎ ‎【题10】一质量为2×103 kg的小汽车从倾斜路面上以20 m/s的速度经A点驶入泥泞的水平路面，行驶200 m路程后到达B点，速度降为5 m/s，此后速度保持恒定，已知整个过程中汽车发动机的输出功率恒为40 kW。求：‎ ‎（1）在泥泞路面上行驶时，汽车受到的阻力；‎ ‎（2）速度为10 m/s时，汽车的加速度。‎ ‎【答案】（1）8 000 N（2）2 m/s2‎ ‎2．以恒定牵引力起动 由于牵引力F恒定，根据牛顿第二定律F–f=ma，可知：加速度a恒定，汽车作匀加速直线运动，随着时间的推移，实际功率将不断增大．由于汽车的实际功率不能超过其额定功率，汽车的匀加速直线运动只能维持到其实际功率等于其额定功率时，此时汽车的速度达到它匀加速直线运动阶段的最大速度v1m，其后汽车只能以额定功率起动的方式进行再加速，其运动方式和第一种起动形式完全相同，即汽车继续做加速度越来越小的变加速直线运动，直至汽车进入匀速直线运动状态，速度达到最终的最大速度vm。汽车的起动过程经历了两阶段：一是匀加速直线运动阶段，二是变加速直线运动阶段，最终做匀速直线运动，其速度–时间图像如图所示。‎ ‎【题11】质量为2000 kg、额定功率为80 kW的汽车，在平直公路上行驶的最大速度为20 m/s。若汽车从静止开始做匀加速直线运动，加速度大小为2 m/s2，运动中汽车所受阻力的大小不变。求：‎ ‎（1）汽车所受阻力的大小；‎ ‎（2）3 s末汽车的瞬时功率；‎ ‎（3）汽车做匀加速运动的时间；‎ ‎（4）汽车在匀加速运动中牵引力所做的功 ‎【答案】（1）4000 N（2）4.8×104 W（3）5 s（4）2×105 J ‎（4）匀加速运动阶段牵引力为恒力，故牵引力所做的功为W＝Fl＝F·at2＝8000××2×52 J＝2×105 J。‎ ‎3．处理以恒定牵引力启动问题的注意点 ‎（1）解决这一类问题关键是要理解额定功率、实际功率的关系，汽车在匀加速运动过程中，实际功率是变化的，并不恒定。‎ ‎（2）汽车在匀加速直线运动阶段，汽车的瞬时速度vt=v0+at（v0=0）；汽车做匀加速直线运动所能维持的时间t1=v1m/a 。‎ ‎（3）汽车在匀加速直线运动阶段，汽车的瞬时功率Pt=Fvt＜P额。‎ ‎（4）汽车在匀加速直线运动阶段结束时，瞬时功率pt等于额定功率P额，且满足pt=P额=Fv1m。‎ ‎（5）汽车在变加速直线运动阶段功率恒为额定功率，进入匀速直线运动时牵引力和阻力平衡，有pt=P额=Fvm。‎ ‎（6）从能的角度看：对于匀加速直线运动阶段，根据动能定理有 （W牵、S 1分别表示匀加速运动阶段牵引力所做的功、位移 ），变加速直线运动阶段牵引力所做的功W'牵= P额t2（t2表示变加速直线运动阶段所经历的时间）， （为变加速直线运动阶段的位移）。‎ 三、机车启动问题中几个物理量的求法 ‎1．分析机车启动问题时的注意事项 ‎（1）机车启动的方式不同，机车运动的规律就不同，因此机车启动时，其功率、速度、加速度、牵引力等物理量的变化规律也不相同，分析图象时应注意坐标轴的意义及图象变化所描述的规律。‎ ‎（2）在用公式P＝Fv计算机车的功率时，F是指机车的牵引力而不是机车所受到的合力，也不是阻力。‎ ‎（3）恒定功率下的加速一定不是匀加速，这种加速过程发动机做的功可用W＝Pt计算，不能用W＝Fl 计算（因为F是变力）。‎ ‎（4）以恒定牵引力加速时的功率一定不恒定，这种加速过程发动机做的功常用W＝Fl计算，不能用W＝Pt计算（因为功率P是变化的）。‎ ‎（5）匀加速过程结束时机车的速度并不是最后的最大速度。因为此时F>F阻，所以之后还要在功率不变的情况下变加速一段时间才达到最后的最大速度vm。‎ ‎（6）瞬时加速度的求法：据F＝求出牵引力，则加速度a＝。‎ ‎2．三个重要关系式 ‎（1）无论哪种启动过程，机车的最大速度都等于其匀速运动时的速度，即 （式中Fmin为最小牵引力，其值等于阻力F阻）。‎ ‎（2）匀加速启动持续时间的求法：牵引力F＝ma＋Ff，匀加速的最后速度v′m＝，时间t＝。匀加速过程结束时，功率最大（额定功率），速度不是最大，即v＝＜vm＝。‎ ‎（3）机车以恒定功率运行时，牵引力做的功W＝Pt。由动能定理：Pt－F阻x＝ΔEk．此式经常用于求解机车以恒定功率启动过程的位移大小。‎ ‎【题12】一列火车总质量m＝500 t，发动机的额定功率P＝6×105 W，在轨道上行驶时，轨道对列车的阻力Ff是车重的0.01倍。取g＝10 m/s2‎ （1） 求列车在水平轨道上行驶的最大速度；‎ （2） 在水平轨道上，发动机以额定功率P工作，求当行驶速度为v1＝1 m/s和v2＝10 m/s时，列车的瞬时加速度a1、a2的大小；‎ （3） 列车在水平轨道上以36 km/h的速度匀速行驶时，求发动机的实际功率P′；‎ ‎（4）若列车从静止开始，保持0.5 m/s2的加速度做匀加速运动，求这一过程维持的最长时间。‎ ‎【答案】（1）12 m/s（2）1.1 m/s2 0.02 m/s2（3）5×105 W（4）4 s ‎（2）当v＜vm时，列车做加速运动，若v1＝1 m/s，则F1＝＝6×105 N，‎ 根据牛顿第二定律得a1＝＝1.1 m/s2‎ 若v2＝10 m/s，则F2＝＝6×104 N 根据牛顿第二定律得a2＝＝0.02 m/s2。‎ ‎（3）当v＝36 km/h＝10 m/s时，列车匀速运动，则发动机的实际功率P′＝Ffv＝5×105 W。‎ ‎（4）由牛顿第二定律得F′＝Ff＋ma＝3×105 N在此过程中，速度增大，发动机功率增大，当功率为额定功率时速度为v′，即v′＝＝2 m/s，‎ 由v′＝at得t＝＝4 s。 . ‎ ‎【题13】在检测某种汽车性能的实验中，质量为3×103 kg的汽车由静止开始沿平直公路行驶，达到的最大速度为40 m/s，利用传感器测得此过程中不同时刻该汽车的牵引力F与对应的速度v，并描绘出如图所示的F－图象（图线ABC为汽车由静止到达到最大速度的全过程，AB、BO均为直线）。假设该汽车行驶中所受的阻力恒定，根据图线ABC，‎ ‎（1）求该汽车的额定功率；‎ ‎（2）该汽车由静止开始运动，经过35 s达到最大速度40 m/s，求其在BC段的位移。‎ ‎【答案】（1）8×104 W（2）75 m ‎【解析】（1）题图图线AB表示牵引力F不变即F＝8 000 N，阻力F阻不变，汽车由静止开始做匀加速直线运动；图线BC的斜率表示汽车的功率P不变，达到额定功率后，汽车所受牵引力逐渐减小，汽车做加速度减小的变加速直线运动，直至达到最大速度40 m/s，此后汽车做匀速直线运动。‎ 由题图可知：当达到最大速度vmax＝40 m/s时，牵引力为Fmin＝2 000 N 由平衡条件F阻＝Fmin可得F阻＝2 000 N由公式P＝Fminvmax得额定功率P＝8×104 W。‎ ‎（2）匀加速运动的末速度vB＝，代入数据解得vB＝10 m/s 汽车由A到B做匀加速运动的加速度为a＝＝2 m/s2设汽车由A到B所用时间为t1，由B到C所用时间为t2，位移为x，则t1＝＝5 s，t2＝35 s－5 s＝30 s B点到C点，对汽车由动能定理可得Pt2－F阻x＝mvC2－mvB2，代入数据解得x＝75 m。‎ ‎【题14】一起重机的钢绳由静止开始匀加速提起质量为m的重物，当重物的速度为v1时，起重机的功率达到最大值P，以后起重机保持该功率不变，继续提升重物，直到以最大速度v2匀速上升，重物上升的高度为h，不计空气阻力，则整个过程中，下列说法正确的是 A． 钢绳的最大拉力为 ‎ B． B．钢绳的最大拉力为mg C． 重物匀加速的末速度为 ‎ D． D．重物匀加速运动的加速度为－g ‎【答案】D