- 2021-05-19 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏教版数学八年级上册课件3-3勾股定理的简单应用
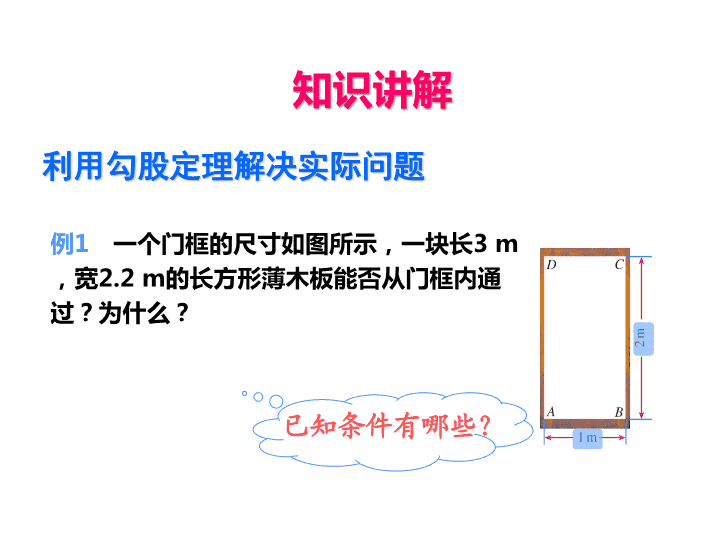
3.3 勾股定理的简单应用 提问 这节课我们就来学习用勾股定理解决实际问题. 例1 一个门框的尺寸如图所示,一块长3 m, 宽2.2 m的长方形薄木板能否从门框内通过? 为什么? 已知条件有哪些? 观察 1.木板能横着或竖着从门框通过吗? 2.这个门框能通过的最大长度是多少? 不能 3.怎样判定这块木板能否通过木框? 求出斜边的长,与木板的宽比较. 解:在Rt△ABC中,根据勾股定理, AC2=AB2+BC2=12+22=5. AC= ≈2.24. 因为AC大于木板的宽2.2 m,所 以木板能从门框内通过. 5 例2 如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上, 这时AO 为2.4米. (1)求梯子的底端B距墙角O多少米? (2)如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移 0.5米吗? C O DB A 在Rt△COD中,根据勾股定理, OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15. 解:在Rt△AOB中,根据勾股定理, OB2=AB2-OA2=2.62-2.42=1. OB=1. 3 15 1 77 1 77 1 0 77 OD . . BD OD OB . . . , 1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC 方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距 离(结果取整数). 解: 2 2 2 260 20 40 2 57m AB BC AC . A B C 2.如图,太阳能热水器的支架AB长 为90 cm,与AB垂直的BC长为120 cm. 太阳能真空管AC有多长? 【解析】在Rt△ABC中,由勾股定理,得 AC= = =150(cm). 答:太阳能真空管AC长150 cm. 已知:如图,在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90°,AB=A′B′,AC=A′C′. 求证: ABC≌△A′B′C′. 证明:在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90° 根据勾股定理,得 2 2 2 2BC AB AC ,BC AB AC . 又AB=A′B′, AC=A′C′, ∴BC=B′C′.∴ABC≌△A′B′C′(SSS). 探究 我们知道数轴上的点有的表示有理数,有的表示无理数, 你能在数轴上画出表示 的点吗?13 分析: 13开方就是 ,,如果一个三角形的斜边长为 的话, 问题就可迎刃而解了。 13 13 发现 是直角边分别为2,3的直角三角形的斜边长。13 2 13 3 O 1 2 3 13 A B C 提问 你能用语言叙述一下作图过程吗? 在数轴上找到点A,使OA=3; 作直线l⊥OA,在l上取一点B,使AB=2; 以原点O为圆心,以OB为半径作弧,弧与数轴交于C点, 则点C即为表示 的点。13 下面都是利用勾股定理画出的美丽图形。 1.在数轴上作出表示 的点.17 解:如图的数轴上找到点A,使OA=4,作直线l垂 直于OA,在l上取点B,使AB=1,以原点O为圆心, 以OB为半径作弧,弧与数轴的交点C即为表示 的点. 17 2.如图,等边三角形的边长是6.求: (1)高AD的长; (2)这个三角形的面积. 解:(1)AD⊥BC于D,则BD=CD=3. 在Rt△ABD中,由勾股定理 AD2=AB2-BD2=62-32=27,故AD=3 ≈5.2 3 (2)S= ·BC·AD= ×6×3 ≈15.631 2 1 2 1.求出下列直角三角形中未知的边. 2 2BC AC ,1 3BC AC , AC=8 AB=17 2.直角三角形中,以直角边为边长的两个正方形面 积为7和8,则以斜边为边长的正方形的面积为 . 2 2 2 260 20 40 2 57(m)AB BC AC 15 3.如图,池塘边有两点A,B,点C 是与BA方向成直角的AC方向上的 一点,现测得CB=60m,AC=20m. 求A,B两点间的距离(结果取整数). 4.如图,在平面直角坐标系中有两 点A(5,0)和B(0,4),求这两点间 的距离. 解: 2 2 2 25 4 41OA OB 解:点A即为表示 的点.20 5.在数轴上作出表示 的点.20 6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶 上方3 km处,过了20 s,飞机距离这个男孩头顶5 km.这 一过程中飞机飞过的距离是多少千米? 【解析】在Rt△ABC中, 答:飞机飞过的距离是4 km. BC A 3 5 ? 勾股定理 的应用 化非直角三角形为直角三角形 将实际问题转化为直角三角形模型查看更多