- 2021-05-19 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第13章全等三角形阶段自测五课件新版华东师大版
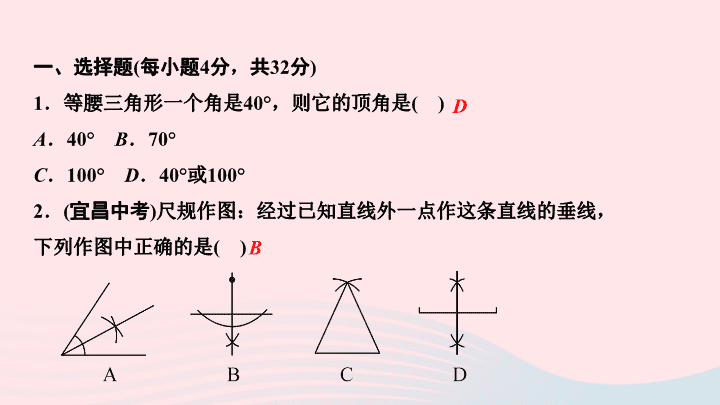
第13章 全等三角形 阶段自测(五) 一、选择题 ( 每小题 4 分 , 共 32 分 ) 1 .等腰三角形一个角是 40° ,则它的顶角是 ( ) A . 40° B . 70° C . 100° D . 40° 或 100° 2 . ( 宜昌中考 ) 尺规作图:经过已知直线外一点作这条直线的垂线, 下列作图中正确的是 ( ) D B 3 .如图,在△ ABC 中,∠ A = 36° ,∠ ABC =∠ ACB , BD 平分∠ ABC , DE∥BC ,则图中的等腰三角形共有 ( ) A . 2 个 B . 3 个 C . 4 个 D . 5 个 4 .如图, OC 平分∠ AOB , CD∥OB ,若 OD = 3 cm ,则 CD 等于 ( ) A . 3 cm B . 4 cm C . 1.5 cm D . 2 cm D A 5 . (2019 · 山西 ) 如图,在△ ABC 中, AB = AC ,∠ A = 30° , 直线 a∥b ,顶点 C 在直线 b 上,直线 a 交 AB 于点 D ,交 AC 于点 E , 若∠ 1 = 145° ,则∠ 2 的度数是 ( ) A . 30° B . 35° C . 40° D . 45° C C 7 . (2019· 潍坊 ) 如图,已知 ∠ AOB. 按照以下步骤作图: ① 以点 O 为圆心,以适当的长为半径作弧, 分别交 ∠ AOB 的两边于 C , D 两点,连接 CD. ② 分别以点 C , D 为圆心,以大于线段 OC 的长为半径作弧, 两弧在 ∠ AOB 内交于点 E ,连接 CE , DE. ③ 连接 OE 交 CD 于点 M. 下列结论中错误的是 ( ) A . ∠ CEO = ∠ DEO B . CM = MD C . ∠ OCD = ∠ ECD C 8 .在等腰△ ABC 中, AB = AC ,中线 BD 将这个三角形的周长 分为 15 和 12 两个部分,则这个等腰三角形的底边长为 ( ) A . 7 B . 11 C . 7 或 11 D . 7 或 10 C 二、填空题 ( 每小题 4 分 ,共 24 分 ) 9 . (2019· 兰州 ) 在△ ABC 中, AB = AC ,∠ A = 40° ,则∠ B = ____°. 10 . ( 无锡中考 ) 命题 “ 两个全等三角形的面积相等 ” 的逆命题 是 _____________________________ . 70 面积相等的两个三角形全等 11 .如图,在△ ABC 中, AB = AC , AD⊥BC ,若 S △ABC = 12 , 则 S △ADC = ___ . 12 . (2019 · 成都 ) 如图,在△ ABC 中, AB = AC ,点 D , E 都在边 BC 上, ∠ BAD =∠ CAE ,若 BD = 9 ,则 CE 的长为 ____ . 6 9 13 .如图,在△ ABC 中,∠ BAC = 120° , 若 PM , QN 分别垂直平分线段 AB , AC ,那么∠ PAQ = _____ ; 如果 BC = 10 cm ,则△ APQ 的周长为 _________ . 60° 10 cm 15 15 . (10 分 ) 如图,两条公路 OA 和 OB 相交于点 O ,在∠ AOB 的内部有工厂 C 和 D ,现要修建一个货站 P ,使货站 P 到两条公路 OA , OB 的距离相等,且到两工厂 C , D 的距离相等,用尺规作出货站 P 的位置. ( 要求:不写作法,保留作图痕迹,写出结论 ) 解:作∠ AOB 的角平分线与 CD 的垂直平分线,两直线相交于点 P , 则点 P 即为所要找的货站的位置.作图略 16 . (10 分 ) 如图,在△ ABC 中, AB = AC , D 为 BC 边上一点, ∠ B = 30° ,∠ DAB = 45° ,求∠ CAD 的度数. 解: 75° 17 . (12 分 ) 有两个全等的含 30° , 60° 角的三角板 ADE 和 ABC , 点 E , A , C 在一条直线上,连结 BD ,取 BD 的中点 M , 连结 ME , MC ,试判断△ EMC 的形状,并说明理由. 解:提示:连结 AM ,先证△ DAB 为等腰直角三角形, 再证△ MDE≌△MAC ,∴ ME = MC ,∠ EMC = 90° , ∴△ EMC 为等腰直角三角形 18 . (12 分 ) 如图, AD 是 BC 边上的中线,∠ ADC = 60° ,把△ ADC 沿直线 AD 折过来,点 C 落在 C′ 的位置,如果 BC = 4 ,求 BC′ 的长.查看更多