2021届高考数学一轮复习第三章导数及其应用创新引领前瞻函数与导数热点问题课件新人教A版
函数与导数热点问题
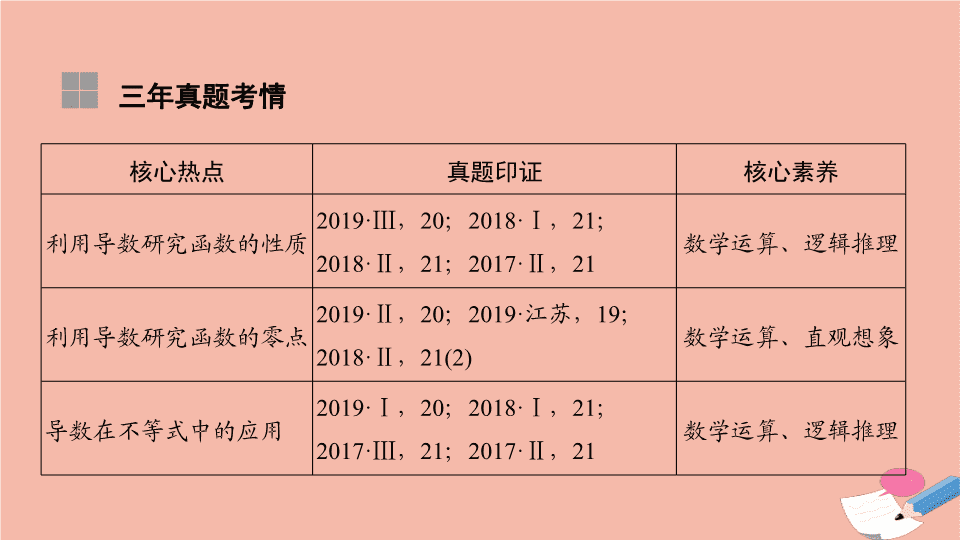
三年真题考情
核心热点
真题印证
核心素养
利用导数研究函数的性质
2019·
Ⅲ
,
20
;
2018·
Ⅰ
,
21
;
2018·
Ⅱ
,
21
;
2017·
Ⅱ
,
21
数学运算、逻辑推理
利用导数研究函数的零点
2019·
Ⅱ
,
20
;
2019·
江苏,
19
;
2018·
Ⅱ
,
21(2)
数学运算、直观想象
导数在不等式中的应用
2019·
Ⅰ
,
20
;
2018·
Ⅰ
,
21
;
2017·
Ⅲ
,
21
;
2017·
Ⅱ
,
21
数学运算、逻辑推理
热点聚焦突破
教材链接高考
——
导数在不等式中的应用
[
教材探究
]
(
选修
2
-
2P32
习题
1.3B
组第
1
题
(3)(4))
利用函数的单调性证明下列不等式,并通过函数图象直观验证
.
(3)e
x
>1
+
x
(
x
≠
0)
;
(4)ln
x
<
x
0).
[
试题评析
]
1.
问题源于求曲线
y
=
e
x
在
(0
,
1)
处的切线及曲线
y
=
ln
x
在
(1
,
0)
处的切线,通过观察函数图象间的位置关系可得到以上结论,可构造函数
f
(
x
)
=
e
x
-
x
-
1
与
g
(
x
)
=
x
-
ln
x
-
1
对以上结论进行证明
.
2.
两题从本质上看是一致的,第
(4)
题可以看作第
(3)
题的推论
.
在第
(3)
题中,用
“
ln
x
”
替换
“
x
”
,立刻得到
x
>1
+
ln
x
(
x
>0
且
x
≠
1)
,进而得到一组重要的不等式链:
e
x
>
x
+
1>
x
-
1>ln
x
(
x
>0
且
x
≠
1).
3.
利用函数的图象
(
如图
)
,不难验证上述不等式链成立
.
【教材拓展】
(
一题多解
)
试证明:
e
x
-
ln
x
>2.
证明 法一
设
f
(
x
)
=
e
x
-
ln
x
(
x
>0)
,
所以当
x
>
x
0
时,
f
′(
x
)>0
;当
0<
x
<
x
0
时,
f
′(
x
)<0.
法二
注意到
e
x
≥
1
+
x
(
当且仅当
x
=
0
时取等号
)
,
x
-
1
≥
ln
x
(
当且仅当
x
=
1
时取等号
)
,
∴
e
x
+
x
-
1>1
+
x
+
ln
x
,
故
e
x
-
ln
x
>2.
【链接高考】
(2017·
全国
Ⅲ
卷
)
已知函数
f
(
x
)
=
ln
x
+
ax
2
+
(2
a
+
1)
x
.
(1)
解
f
(
x
)
的定义域为
(0
,+
∞
)
,
当
x
∈
(0
,
1)
时,
g
′(
x
)>0
;
x
∈
(1
,+
∞
)
时,
g
′(
x
)<0.
所以
g
(
x
)
在
(0
,
1)
上单调递增,在
(1
,+
∞
)
上单调递减
.
故当
x
=
1
时,
g
(
x
)
取得最大值,最大值为
g
(1)
=
0.
所以当
x
>0
时,
g
(
x
)
≤
0
,
教你如何审题
——
利用导数研究函数的性质
【例题】
(2019·
全国
Ⅱ
卷
)
已知函数
f
(
x
)
=
(
x
-
1)ln
x
-
x
-
1.
证明:
(1)
f
(
x
)
存在唯一的极值点;
(2)
f
(
x
)
=
0
有且仅有两个实根,且两个实根互为倒数
.
[
审题路线
]
[
自主解答
]
证明
(1)
f
(
x
)
的定义域为
(0
,+
∞
).
故存在唯一
x
0
∈
(1
,
2)
,使得
f
′(
x
0
)
=
0.
又当
x
<
x
0
时,
f
′(
x
)<0
,
f
(
x
)
单调递减,
当
x
>
x
0
时,
f
′(
x
)>0
,
f
(
x
)
单调递增,
因此,
f
(
x
)
存在唯一的极值点
.
(2)
由
(1)
知
f
(
x
0
)<
f
(1)
=-
2
,又
f
(e
2
)
=
e
2
-
3>0
,
所以
f
(
x
)
=
0
在
(
x
0
,+
∞
)
内存在唯一根
x
=
α
.
综上,
f
(
x
)
=
0
有且仅有两个实根,且两个实根互为倒数
.
探究提高
1.
利用导数研究函数的性质是历年高考的重点、热点,涉及的主要内容:
(1)
讨论函数的单调性;
(2)
求函数的极
(
最
)
值、极
(
最
)
值点;
(3)
利用性质研究方程
(
不等式
).
考查数学运算、逻辑推理、直观想象等数学核心素养
.
2.
本题求解的关键是明确函数的极值点与函数零点之间的联系,充分运用函数的单调性、极值、零点存在定理综合求解,善于把函数的零点转化为方程根的问题
.
(1)
试讨论函数
f
(
x
)
的单调性;
(2)
设
x
1
,
x
2
是
f
(
x
)
的两个极值点,且
x
2
>
x
1
,设
t
=
f
(
x
1
)
-
f
(
x
2
)
-
(
a
-
2)(
x
1
-
x
2
)
,试证明
t
>0.
(1)
解
f
(
x
)
的定义域为
(0
,+
∞
)
,
①
若
a
≤
2
,则
f
′(
x
)
≤
0
,
当且仅当
a
=
2
,
x
=
1
时
f
′(
x
)
=
0
,
所以
f
(
x
)
在
(0
,+
∞
)
上单调递减
.
(2)
证明
由
(1)
知,
f
(
x
)
存在两个极值点时,当且仅当
a
>2.
由于
f
(
x
)
的两个极值点
x
1
,
x
2
满足
x
2
-
ax
+
1
=
0
,所以
x
1
x
2
=
1.
又因
x
2
>
x
1
>0
,所以
x
2
>1.
由第
(1)
问知,
φ
(
x
)
在
(1
,+
∞
)
单调递减,且
φ
(1)
=
0
,
从而当
x
∈
(1
,+
∞
)
时,
φ
(
x
)<0.
满分答题示范
——
利用导数研究函数的零点问题
(1)
讨论
f
(
x
)
的单调性,并证明
f
(
x
)
有且仅有两个零点;
(2)
设
x
0
是
f
(
x
)
的一个零点,证明曲线
y
=
ln
x
在点
A
(
x
0
,
ln
x
0
)
处的切线也是曲线
y
=
e
x
的切线
.
[
规范解答
]
(1)
解
f
(
x
)
的定义域为
(0
,
1)
∪
(1
,+
∞
).
所以
f
(
x
)
在
(0
,
1)
,
(1
,+
∞
)
单调递增
.2
分
所以
f
(
x
)
在
(1
,+
∞
)
有唯一零点
x
1
(e<
x
1
1.
所以
f
(
x
)<0
,从而
f
(
x
)
在
(π
,+
∞
)
没有零点
.
综上,
f
(
x
)
有且仅有
2
个零点
.